администратор: Качено първо на 2011 09 03
Статия от госта Антон Каменов
Дисторшънът в музиката потиска върховете на звуковия сигнал. При аналоговите сигнали това може да се получи, когато сигналът започва да претоварва схемите на устройствата. При цифровите сигнали дисторшъна работи по подобен начин.
Вземи следното просто изчисление на изходния сигнал y(k) от входния сигнал x(k).
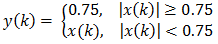
Тази операция се нарича твърдо окастряне (от англ., hard clip). Тя просто ще отреже върховете на една проста синусоида с амплитуда на върха равна на 1 както във фигурата по-долу. Тази фигура съдържа една вълна с честота 100 Hz и амплитуда на върха 1, записана с пробната честота 2000 Hz. Тази вълна е окастрена с горната формула.
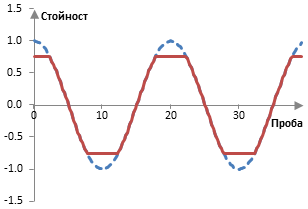
Твърдото окастряне създава дисторшън, но това не е цялата история. Получената вълна вече не е една проста вълна. Тя е един сигнал с някакво честотно съдържание, което е различно от честотното съдържание на оригиналната вълна.
Следната фигура показва честотното съдържание на оригиналната вълна и на сигнала след дисторшъна. Въпреки че входната проста вълна има само един максимум при 100 Hz – честотата на простата вълна – сигнала след дисторшъна има допълнителни максимуми при 300 Hz, 500 Hz и 700 Hz.
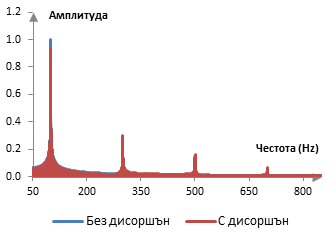
Тези честоти се получават, като се умножи 100 Hz по нечетни цели числа и следователно са нечетните хармоници на 100 Hz. Така, дисторшъна произвежда хармоници. Всяка нелинейна операция със сигнала всъщност ще произведе хармоници. Една нелинейна операция върху сигнала следователно може да се нарече "хармоничен дисторшън". Колкото е по-щателно окастрянето (т.е., 0.5 вместо 0.7), токова по-подчертани ще бъдат хармониците.
Едно рязко окастряне на върховете на сигнала не е единствения начин да се получи дисторшън. Един по-мек дисторшън може да се получи като върховете на сигнала се потиснат бавно. Следното меко кубично окастряне е една добре позната операция, която прави точно това.
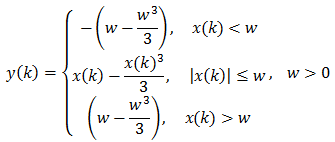
Крайният ефект на мекото кубично окастряне на една проста вълна е показан по-долу. При по-големи w, окастрянето става по-меко и е по-близо до върха на вълната. Мекото кубично окастряне създава подобни нечетни хармоници в сигнала.
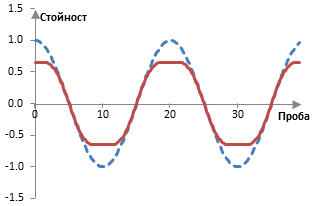
Съществуват много операции, които можем да използваме за да окастрим сигнала. Окастрянето обаче не е задължително. Следната операция за дисторшън потиска върховете на сигнала без да ги кастри. А и произвежда същите нечетни хармоници, само че с по-малка енергия.
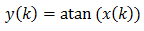
Интересно е, че кастренето и компресирането на върховете на сигнала винаги произвежда нечетни хармоници. Виж следната фигура, която показва един сигнал със 100 Hz с амплитуда на върха 1 (синя прекъсната линия) и сумата на този сигнал на 100 Hz с един сигнал с честота 300 Hz с амплитуда 0.3 (червена линия).
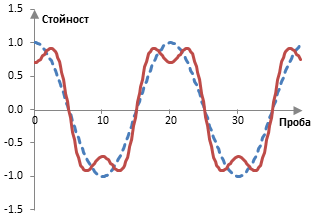
Ефекта на добавянето на една проста вълна с честота равна на три пъти на честотата на оригиналната вълна и с по-ниска амплитуда е доста подобен на окастрянето на вълната. Така, нечетните хармоници при дисторшъна не могат да се избегнат.
Ако искахме да произведем четни хармоници – оригиналната честота умножена по четни цели числа – можем да прегледаме ефекта на сумата на две вълни, едната от които например е с честота два пъти по-голяма от честотата на другата вълна – първият и четен хармоник. Сумата на тези две вълни е показана в следната графика.
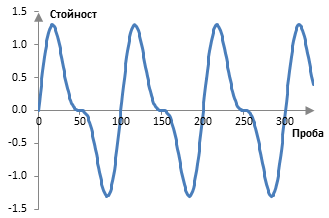
Четните хармоници не потискат (компресират), а разтягат (декомпресират) върховете на сигнала. Също така, сигналът става несиметричен – за разлика от добавянето на първия нечетен хармоник, което дава един доста симетричен сигнал.
Една от операциите, които са добри кандидати за произвеждането на нечетни хармоници, е
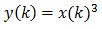
Можеш да видиш, че тази функция дава и четни, и нечетни хармоници. Ако окастрим този сигнал, ще получим един доста различен дисторшън.
Следната операция също е интересна.
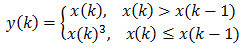
Тази операция произвежда само четни хармоници с изключение на първия нечетен хармоник с честота равна на три пъти оригиналната честота, както по-долу.
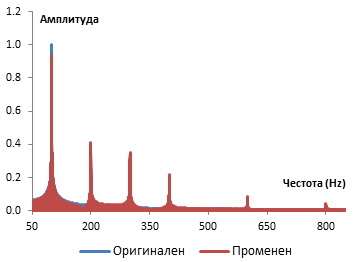
Единственият проблем с тази операция е че тя не е безпаметна. Трябва да използва предишните проби на сигнала.
На практика, цифровият дисторшън може да е една доста проста операция, както тези по-горе или пък по-сложен. Например, дисторшъна може да трябва да увеличи пробната честота на данните с аудио. Това може да е необходимо, защото хармониците на високите записани честоти може да са по-високи от честотата на Найкуист и Шанон при оригиналната пробна честота. Ако се увеличи пробната честота, сигналът се пресъздава, но със по-висока пробна честота, което означава, че честотата на Найкуист и Шанон също е по-висока. Цифровият дисторшън може да използва и един еквилайзер за да контролира амплитудата на хармониците. Също така, дисторшъна може да бъде различен за различните части на честотния диапазон, като оригиналният сигнал се разделя на няколко части – например на ниските, средните и високите честоти.
Добави нов коментар