администратор: Качено първо на 2012 07 27
Статия на госта Антон Каменов
Филтрите и другите операции при работата с цифрови сигнали (DSP) за аудио са прегледани в детайли в този сайт. Съществуват различни операции за DSP и следната дискусия важи за всички тях, независимо от това, че когато инженерите говорят за грешките в DSP, обикновено имат предвид филтрите – филтрите с ограничени импулсни спектри, филтрите с неограничени импулсни спектри и т.н.
Грешките в DSP и квантуването
Добре е да отбележим, че можем да срещнем няколко различни вида грешки, когато създаваме DSP операции. Първо, операцията може да има неправилна или, по-често, непрецизна спецификация. Една непрецизна спецификация може например да закръгли коефициентите на един филтър. Тези грешки обикновено са почти незабележими. Една грешка в четвъртата цифра след запетайката в един от коефициентите на един високочестотен филтър на Бесел от трети разряд с преходна честота 6000 Hz не дава забележими промени в честотния спектър на един сигнал с пробна честота от 44.1 Hz след 20 секунди. Така или иначе, хубаво е да обърнем внимание на прецизността на спецификацията на филтъра.
Грешките може да се получат от изчислителната прецизност. Съвременният софтуер обаче обикновено е точен поне до 15 цифри след десетичната запетайка при 8 битовата представяне на числата и около 7 цифри след десетичната запетайка при 4 битовото представяне. Тези грешки също ще са незабележими.
Други грешки се получават при квантуването. При работата с цифрови сигнали, квантуването е превръщането на едно голямо множество от стойности в едно по-малко множество. При аудиото, това обикновено е взимането на проби, при което един аналогов сигнал, амплитудата на който може да има безкрайно много възможни стойности, се превръща в дискретизиран сигнал с краен брой възможни стойности. Аудиото с качество на един диск (CD) например използва 16 битови означени цели числа и се записва с целите числа между -32768 и 32768. Така, ако изчисленията за DSP използват представянето на аудио CD-то, сигналът ще бъде закръглен (нагоре или надолу) или просто отрязан (надолу) до тези цели числа.
Квантуването създава два вида проблеми. Първо, работата със сигнала при DSP-то може да е неправилна. При един филтър с неограничен импулсен спектър например, не е хубаво да закръгляваме или отрязваме стойностите на изходния сигнал, преди работата с този изходен сигнал да е свършила. С други думи, не е добре да закръглим стойността на y(k – 1), докато тази стойност не е използвана за да се изчислят y(k), y(k + 1) и т.н. Можем да си представим, че едни такива грешки могат да се натрупат при този тип филтри, тъй като те ще върнат погрешно изчисления изходен сигнал обратно към входа. При 16 битовите цели числа, същият филтър на Бесел от трети разряд в примера по-горе, след 20 секунди, дава промяна в амплитудния спектър около преходната честота от около -0.002, а и малко по-малко в преходната лента. Тази промяна е малка, но все пак забележима. Също така, очакваме, че размера на грешката ще стане по-голям с един по-дълъг аудио сигнал, по-висока пробна честота или пък по-малка пробна резолюция.
Второ, квантуването понякога е неизбежно. Аудиото с качеството на едно CD в края на краищата ще съдържа закръглени или отрязани стойности. Трудно е да направим едно проучване на ефекта на това отрязване с пробната честота 44100 Hz и 16 битовото представяне и затова ще използваме по-ниска пробна честота и резолюция. Вземи една вълна от 2 Hz (в синьо) при пробната честота 100 Hz, стойностите на която са представени с 4 бита (в червено). Въпреки че истинската стойност на вълната при проба 5 е 4.702, тя е записана като 5. Въпреки че истинската стойност на вълната при проба 6 е 5.476, тя също е записана като 5. Както е показано в графиката по-долу, не е възможно да запишем истинската стойност на вълната при пробната резолюция от 4 бита.
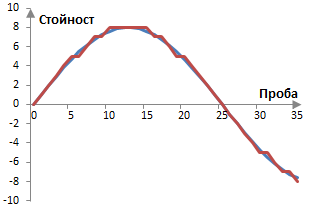
Специалистите може би ще спорят дали такива грешки при квантуването са доловими в един запис на аудио (грешките на квантуването са доста забележими при някои цифрови картинки, като например файловете GIF, при които резолюцията на цветовете позволява само 256 цвята). Така или иначе, ясно е, че тези грешки са систематични, количествено измерими и неизбежни. Ако по-горният сигнал се повтори безкрайно, грешките също ще бъдат повторени безкрайно, точно по същия начин. Грешките от този вид тогава са периодични, със същия период като сигнала, и с корелация към сигнала. С други думи, грешката е хармонична дисторция (изкривяване) на сигнала.
Грешките при квантуването най-вероятно ще се появят при всички операции за DSP и могат да съществуват във входния записан сигнал. Тъй като тези грешки са малки, ако са доловими, най-вероятно ще са доловими когато сигналът е записан с ниски нива и когато тези нива след това са повишени. Тези грешки са специфични за пробната честота, резолюцията и сигнала. Различни грешки ще се появят при други сигнали, пробни честоти или резолюции.
Дитер
Тъй като грешките при квантуването са неизбежни, най-доброто, което можем да направим, е да ги направим такива, че да не са систематични. Грешките, които не са систематични, няма да са хармонична дисторция на сигнала. Можем да направим това, като дадем някакъв случаен шум в сигнала, с амплитуда приблизително равна на амплитудата на грешката. Дитеринг е този процес, при който случаен шум се пуска в една система за да премахне грешки, между които и сигнала има корелация.
Въпреки че дитера не премахва грешките, поне прави така, че между тези грешки и сигнала да няма корелация. Ако пуснем сигнала в по-горната графика през един дитер, може би ще получим нещо като в графиката по-долу. Тази графика се получава, когато случайно изберем дали да закръглим стойностите на вълната нагоре или надолу. Това е същото, като да добавим едно случайно число между -0.5 и 0.5 към вълната и тогава да закръглим нагоре или надолу както е подходящо. Това е най-простия дитер – този, който използва равномерното разпределение на случайната промяна в грешката и който се прилага със пробната честота.
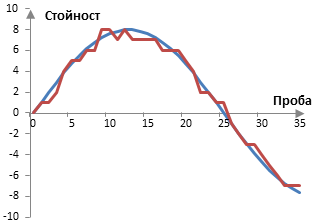
Има няколко начина, по които можем да променим дитера. Първо, този дитер използва равномерно разпределение на добавената грешка и следователно се казва, че използва функция с квадратна вероятностна плътност (от англ., "rectangular probability density function" или RPDF). Често срещаните дитери при работата с аудио сигнали са или дитери RPDF или такива, които използват функция с триъгълна вероятностна плътност (от англ., "triangular probability density function" или TPDF) (дитерите RPDF би трябвало да премахват корелацията на първия момент на грешката, а дитерите TPDF трябва да премахват първия и втория момент на грешката). Възможни са и други вероятностни плътности.
Дитерът може да бъде променен и като се въведат грешки с различна честота, което обикновено се нарича оцветяване на дитера. Целта на това обикновено е да се въведат грешки, които са извън диапазона, в който ухото е най-чувствително, като например извън интервала от 1 KHz до 5 KHz (Трябва обаче да отбележим, че нивата на кривите на чуване (кривите на Флетчер и Мансън) винаги зависят от нивата на сигнала и няма интервали, в които чувствителността на ухото е независима от нивото на сигнала). Това може да се направи просто като случайния дитер се пусне през един филтър. Това също се нарича оформяне на шума, въпреки че има разлики между оцветяването на дитера и оформянето на шума. Оформянето на шума може да се използва и за да се променят съществуващите грешки на квантуването без изобщо да се използва дитер.
Можем и да променим амплитудата на дитера. Сигналът след дитера в по-горната графика променя оригиналния квантуван сигнал като добавя един бит при случайни проби, като изважда един бит или пък като оставя записаната стойност на сигнала непроменена. С други думи, този дитер работи като променя най-ниските – най-маловажните – битове в сигнала и затова се нарича операция върху най-маловажния бит (от англ., "least significant bit" или LSB). Нормално е да се използва шум от един или два бита.
Дитера не е нещо, което трябва да се използва прекалено много или пък случайно. Първо, няма грешки на квантуването, когато няма сигнал. Не трябва да използваме случаен шум ако няма систематичен шум, като например между пистите с аудио. Или пък, трябва да използваме дитер, който е такъв, че да стане нула, когато сигнала става нула. Накрая, дитера обикновено не се използва в сигнали, които ще бъдат преработени, защото може да се получат взаимодействия между дитера в тези сигнали и дитерите, които се използват след това.
Един пример на оформянето на шума
Оформянето на шума може да се приложи по време на квантуването, когато грешката в сигнала се знае. Да предположим, че сигналът x0(k) е квантуван и става сигнала x(k) и грешката преди оформянето на шума е ε0(k).
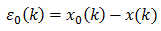
Можем да пуснем грешката ε(k) през един филтър и да създадем една нова стойност след квантуването X(k), като например следната.
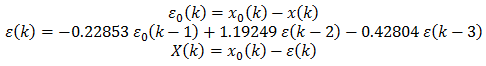
Може би ще забележиш, че новата грешка ε(k) е изчислена с импулсно инвариантния филтър на Батъруърт от втори разряд с ъглова преходна честота 0.6.
На практика, по-често се използват редуцирани изчисления, като например следното
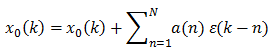
където a(n) са някакви коефициенти на филтъра за филтрираната решка. В най-простия случай, формулата
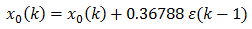
е просто изчисление на грешката с
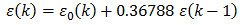
Това е просто импулсно инвариантния филтър на Батъруърт от първи разряд с преходна честота 1.
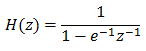
автори: mic
Добави нов коментар