Импулсен ривърб с деконволюция – Част 1 – един примерен импулсен спектър на ривърба

администратор: Качено първо на 2013 08 31

Това трябва да е статия за деконволюцията на един реалистичен запис на някакъв ревербериран звук, с която можем да получим импулсния спектър на ривърба, но засега нямаме средствата да направим това. За да стигнем дотам, ще трябват няколко статии. Когато сме готови – и ако успеем – ще имаме една доста добра имитация на един естествен ривърб и би трябвало да можем да използваме получения импулсен спектър за да симулираме естествения ривърб върху всякакви записи.

Във всяко пространство, можем да запишем един къс звук – плясване с ръце, удар по един барабан, изстрел – заедно с естествените реверберации на пространството. Ако можем да отделим оригиналния звук, като например го запишем отделно с един микрофон, който не усеща (или усеща само част от) реверберациите, ще можем да определим броя и разпределението на повторенията на сигнала в реверберираната част. Тогава ще имаме и един модел на естествената реверберация. Ако тази реверберация е хубава, ще можем да използваме модела за да симулираме тази хубава реверберация при други записи.

За да проверим тази теория, първо ще създадем един импулсен спектър на някакъв примерен ривърб. Този реверб не трябва да е супер и даже и не трябва да е реалистичен. Ще бъде нещо, което можем първо да използваме за да създадем един ревербериран звук и след това да използваме реверберирания звук за да създадем импулсния спектър отново. Ще използваме две неща. Един многоизходен дилей ще моделира ранните отражения (повторения) на ривърба – отражения, които са малко на брой и които са горе долу далече едно от друго. Един ривърб на Шрьодер ще моделира късната част на ривърба – много на брой отражения които са близо едно до друго и които може би имат няколко върхове и падини.

Многоизходният дилей обикновено се изписва по следния начин

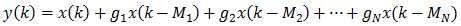
където M₁, M₂, …, M_N са стойностите на забавянията (в брой проби) и g₁, g₂, …, g_N са амплитудите (затихванията). За да опростим нещата, ще използваме само две повторенията. Също така ще махнем x(k) от уравнението за да работим само с реверберацията без оригиналния сигнал. Можем да добавим оригиналния сигнал по-късно. Следната графика показва импулсния спектър на многоизходния дилей с два изхода, един с амплитуда 0.7 и забавяне от 43 милисекунди (ms) и един с амплитуда 0.5 и забавяне равно на 67 ms. В цялото това упражнение, ще използваме пробната честота 2000 Hz, което означава, че първият изход има забавяне от 86 проби и вторият изход използва забавяне равно на 134 проби.

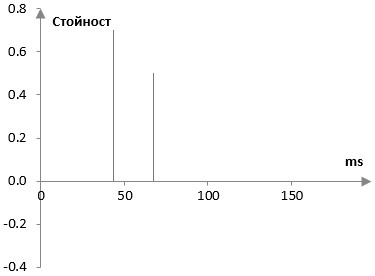
Този модел на ранните повторения е достатъчно прост. Моделът на ривърба на Шрьодер за късните реверберации се състои от една поредица от последователни всичкопропускащи филтри на Шрьодер следвани от няколко паралелни напредващи гребенови филтри. Всичкопропускащите филтри използват формулата

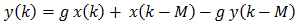
където M е стойността на забавянето в проби и g е промяната в амплитудата. Те създават много затихващи повторения на сигнала. Гребеновите филтри са просто

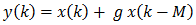
където, пак, M е стойността на забавянето в проби и g промяната в амплитудата. Тези гребенови филтри създават върхове и падини в повторенията в късната реверберация. Ще ги видим по-долу. Ще създадем една проста късна реверберация – само с два всичкопропускащи филтри и един гребенов филтър.

Първо, трябва да решим точно какво трябва да пуснем през реверберацията на Шрьодер – оригиналния сигнал или изхода от многоизходния дилей. Можем да пуснем каквото и да е, но с оригиналния сигнал ще получим изходен сигнал, с който по-лесно можем да работим и да настроим. Параметрите, които ще изберем за многоизходния дилей или за всичкопропускащите и гребеновите филтри, не са случайни. Ще ги настроим в зависимост от това, което видим, но за това после.

Следната графика показва изхода от първия всичкопропускащ филтър. Този филтър има M = 3.7 ms и g = 0.7. Тъй като пробната честота е 2000 Hz, 3.7 ms дават забавяне равно на 7 проби. Ще запазим мащаба на вертикалната ос един и същ във всички графики, за да можем по-лесно да ги разберем. Тъй като пускаме оригиналния сигнал през всичкопропускащите филтри, ще трябва първо и да забавим, и да затихнем сигнала. Най-вече за да получим една хубава графика и донякъде ако предположим, че повторенията стават все по-близки едно до друго, когато реверберацията се развива, ще забавим оригиналния сигнал с 83 ms. Така, разликата между оригиналния сигнал и първия изход на многоизходния дилей е около 40 ms, разликата между първия и втория изход от многоизходния дилей е около 25 ms и разликата между втория изход на многоизходния дилей и вичкопропускащите филтри е около 15 ms. Тъй като двата всичкопропускащи филтри вече идват със затихвания (и двете са около 0.7), ще използваме нещо, което ще ни даде експоненциално затихване от оригиналния сигнал до първия изход, до втория изход и до всичкопропускащите филтри – 0.7.

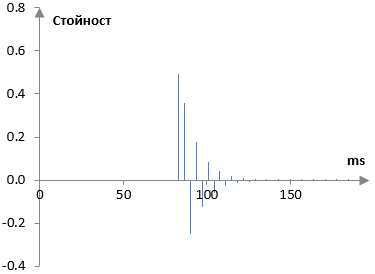
Ще вземем този изходен сигнал и ще го пуснем през втория всичкопропускащ филтър. Вторият всичкопропускащ филтър има g = 0.65 и M = 1.23 ms (3 проби). Той произвежда много допълнителни повторения. Комбинацията от двата всичкопропускащи филтри е показана на следната графика.

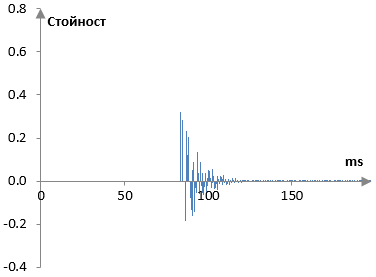
Изходния сигнал на втория всичкопропускащ филтър става входен сигнал за гребеновия филтър. Той има g = 0.7 и забавяне равно на M = 11 ms (23 проби). Този единствен гребенов филтър дава един връх в повторенията. Изходният сигнал от този филтър е и късната реверберация – изходния сигнал на ривърба на Шрьодер.

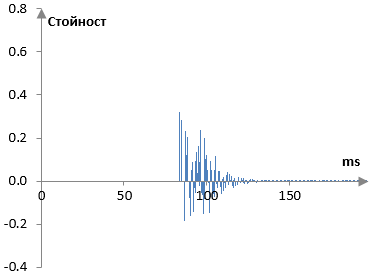
Накрая, импулсният спектър на целия ривърб просто е сумата от изходите на многоизходния дилей и ривърба на Шрьодер (оригиналният сигнал все още не е тук; можем да го добавим когато и да е).

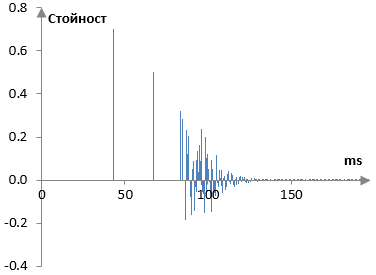
Това е импулсният спектър на целия ривърб. В следващата статия ще пуснем един измислен удар по барабана през същите тези филтри, а и през една конволюция с този импулсен спектър за да видим дали реверберираните барабани са едни и същи.

автори: mic