Импулсен ривърб с деконволюция – Част 3 – деконволюцията

администратор: Качено първо на 2013 09 28

Това е третата статия за деконволюцията на реверберирания звук за да се получи импулсния спектър на естествената реверберация. Ако можем да го направим, ще можем да използваме импулсния спектър като изкуствения ривърб. В първата статия създадохме един примерен импулсен спектър на един ривърб. Във втората статия, използвахме импулсния спектър за да видим какво ще стане с един удар по барабаните след ривърба. В тази статия ще направим обратното. Ще се опитаме да получим оригиналния импулсен спектър, като предположим, че имаме само оригиналния удар по барабана и реверверирания удар по барабана.

Идеята по принцип беше: отиваме в една стая, която има хубава естествена реверберация. Записваме един кратък звук – един удар по барабаните – ревербериран и сух. Изчисляваме импулсния спектър на естествените реверберации от двата сигнала и имаме един хубав импулсен спектър, който можем да използваме за да реверберараме каквото и да е.. Предишните две статии просто ни подготвиха за тази статия – създадохме един импулсен спектър и един ревербериран удар по барабаните – всичко това само заради тази статия.

В този нереален случай

В нашия нереален, изкуствен случай, задачата ни е лесна. Конволюцията y(k) е изчислена както в следната графика (импулсният спектър a(k) отляво и удара по барабана x(k) отдясно).

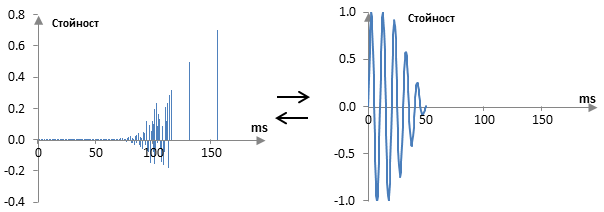
Тогава първата проба на конволюцията y(0) е изчислена само от една проба на импулсния спектър a(0) и една проба на удара по барабана x(0), втората проба на конволюцията е изчислена само от по две проби от импулсния спектър и удара по барабаните и така нататък. Получаваме

a(0) = y(0) / x(0)
a(1) = (y(1) – a(0) x(0)) / x(1)
a(2) = (y(2) – a(0) x(0) – a(1) x(1)) / x(2)
…

В нашия изкуствен случай, можем да изчислим импулсния спектър от конволючията и барабана с прости алгебрични операции.

В реалния случай

В реалния случай, нещата не са точно такива и можем да срещнем проблеми. Може да ни е трудно да различим сухия от реверберирания звук. Можем да вземем два микрофона, един от които може да запише оригиналния удар по барабаните и реверерацията и един, който ще запише само оригиналния удар. Не можем да гарантираме обаче, че микрофоните ще запишат сухия сигнал по един и същи начин, защото всеки микрофон ще добави някаква собствена специфична окраска към сигнала. Също така, втория микрофон може все пак и да запише част от реверберирания сигнал, независимо от това, колко се опитваме да предотвратим това. Крайният резултат е – може би няма да можем да използваме същите изчисления за да получим импулсния спектър.

Ако използваме оригиналните данни в изкуствения пример по-горе, можем да добавим някакви случайни грешки в сухия удар по барабана за да го направим малко по-различен от удара по барабана, който се съдържа в реверберирания сигнал. Това ще симулира различната окраска на двата микрофона. За примера по-долу, средната грешка във всяка от пробите е около 5% от оригиналния сигнал (нагоре или надолу. Алгебричните изчисления произвеждат един импулс (в червено по-долу), който е почти същия, като оригиналния (в синьо), въпреки че все пак е, естествено, различен.

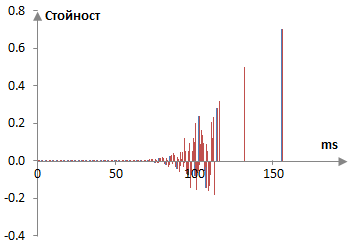
Тъй като сега в алгебричните изчисления по-горе доста от пробите не са нула, както би станало, ако използвахме чистите сигнали без случайните грешки, имаме доста повече проби в импулса, които не са нула.

Една алтернатива на аглебричната деконволюция е оптимирането. Идеята е да намерим импулсния спектър, който, когато е приложен върху оригиналния сигнал, произвежда един сигнал, който е възможно най-близо до реверберирания сигнал. Ако се опитаме да направим това, можем да получим един импулсен спектър, който е доста грозен.

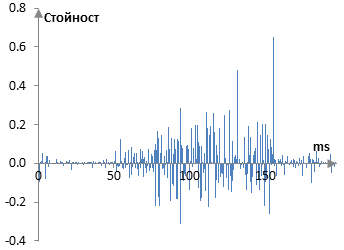
Това ли е правилния импулсен спектър или онзи по-горе е по-добър? Алгебричните изчисления ни дадоха един импулсен спектър, който изглежда по-подобен на оригиналния, то това не е важно. Важното е, че и двата импулсни спектри ни дават един ревербериран сигнал, който е подобен (почти същия) както сигнала с "естествената" реверберация, който получихме в предишната статия.

При оптимирането, разбира се, имаме избор. Можем да оптимираме един импулсен спектър или пък можем да оптимираме една сбирка от всичкопропускащи филтри на Шрьодер и гребенови филтри. Имаме и проблем с оптимирането тук. Нашият сигнал, който трябва да представлява удара по барабана, е прекалено "чист". В този неестествен пример, удара по барабана е една проста синусоида. Сигурно затова оптимирания импулсен спектър съдържа прекалено много "шум". Две ненулеви проби една до друга например ще произведат резултат, който е същия, като една ненулева проба с двоен размер. В един по естествен пример това сигурно няма да стане. Един естествен сигнал би трябвало да съдържа много на брой различни честоти.

автори: mic