Бележки за как да създадем транспонирането

администратор: Качено първо на 2016 07 12

Статия на госта Антон Каменов

Най-простият начин да променим тоналността на един сигнал е просто да го разтеглим или свием във времето. Този вид транспониране обаче има един недостатък, защото и променя темпото на сигнала – забързва го или го забавя. Все пак може да е полезно, ако сигналът е кратък или пък ако темпото му не е важно. Може да се използва например при промяната на тона на семпли за барабани, които се използват в барабанните машини или пък при семплите wave в устройствата MIDI.

Операцията

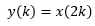
например ще вземе един сигнал x(k) с дължина T и ще го скъси в един сигнал y(k) с дължина T / 2. Циклите на всяка честота в сигнала ще станат два пъти по-малки, което ще направи всяка честота два пъти по-голяма и ще транспонира сигнала с една октава нагоре. Пробите на сигнала x(k) ще бъдат половината от оригиналните проби и, на теория, това може да се направи за каквото и да е отношение за да се получи каквато и да е промяна в тоналността. Ако x(k) е цифровия запис на една песен, тогава y(k) ще бъде същата песен с една октава нагоре, но и с два пъти по-бързо темпо.

По-добро транспониране

Дискретизираното преобразуване на Фурие (discrete Fourier transform, DFT) ни позволява да разложим сигнала на компоненти с прости вълни с позната честота, амплитуда и фаза. Можем да променим тези компоненти, като променим техните честоти и след това можем да използваме обратното дискретизирано преобразуване на Фурие върху тези компоненти за да изградим един нов сигнал.

DFT има два недостатъка. Първо, не можем да го използваме върху дълги части на сигнала, защото композицията на сигнала може да се промени – един запис на един музикален инструмент може да свири различни ноти или същите ноти но с различна амплитуда в различни точки във времето. Стойностите на амплитудата и фазата, които ще получим от преобразуването, дават добра информация за кратки периоди от време, но нямат смисъл за по-дълги периоди. Обратното преобразуване ще изгради един транспониран сигнал, който не се променя във времето. Ако искаме да използваме DFT, ще трябва да го направим върху малки части на сигнала.

Второ, преобразуването не може да ни даде амплитудата и фазата на всички честоти в сигнала. Може да направи това само за един дискретен комплект от честоти с брой равен на дължината на преобразуването. Това означава, че преобразуването не е перфектно. Произвежда амплитуди и фази даже и върху прости вълни с честоти, които не са точно в комплекта с честоти на преобразуването. Една проста вълна с честота 40 Hz например може да се покаже с някаква амплитуда при 50 Hz, ако използваме DFT при 0 Hz, 50 Hz, 100 Hz и т.н. Трябва да намерим начин да правим разлика между честотите на преобразуването и действителните честоти в сигнала.

За да се справим с прецизността при честотите

Ще използваме един прост пример. Вземи един сложен сигнал, който се състои от три прости вълни (прости синусоиди) с честоти 40 Hz, 222 Hz и 465 Hz, съответно със забавяния от 8, 3 и 2 проби и с амплитуди (на върховете) 0.3, 1.2 и 0.8 и предположи, че този сигнал е записан с пробната честота 1000 Hz. Тези три прости вълни може да са 0.3 sin(2π 40 (k – 8) / 1000), 1.2 sin(2π 222 (k – 3) / 1000) и 0.8 sin(2π 465 (k – 2) / 1000). Тъй като вълната с честота 40 Hz има цикъл равен на 1000 / 40 = 25 проби, забавянето от 8 проби при честотата 40 Hz е всъщност забавяне от 8 / (1000 / 40) = 0.32 части от цикъла на вълната или or 2π 0.32 = 2.01 радиани. По същия начин, фазата на вълната при 222 Hz е 4.19 радиани и фазата на вълната при 465 Hz е 5.84 радиани.

Предположи, че имаме цифровия запис на този сложен сигнал и не знаем нищо за простите вълни в него (т.е., не знаем техните точни честоти или фази). Започваме, като вземаме един кратък, да кажем от 40 точки, DFT върху първите 40 проби на сигнала. Тъй като работим с пробната честота 1000 Hz, едно преобразуване с 40 точки ще ни даде информация за амплитудите и фазите за 40 компонента равно разпределени между 0 Hz и 1000 Hz, тоест 0 Hz, 25 Hz, 50 Hz, …, 975 Hz. При 25 Hz и 50 Hz например, компонентите ще имат амплитудите съответно 2.41 и 5.05. Съответните фази ще са 1.89 и -1.53 radians. Можем да предположим, че истинската проста честота, която съществува в сигнала, е някъде между 25 Hz и 50 Hz, но в момента нямаме достатъчно информация да знаем каква е точно.

Продължаваме, като вземаме DFT от 40 точки върху следващите 40 проби в сигнала. Получаваме амплитуда и фаза от 3.22 и -2.45 при 25 Hz и 4.59 и 1.30 при 50 Hz. Фазата при 50 Hz започна при -1.53 и стана -1.30. Очаквахме, че една вълна при 50 Hz, която има цикъл от 1000 / 50 = 20 проби и започва с -1.53 радиани, ще остане с -1.53 радиани след 40 проби, като пренебрегнем два пълни цикъла от 4π. Вместо това получаваме -1.30 радиани. Можем да използваме тази разлика във фазата за да изчислим приблизително истинската честота, която се съдържа в сигнала.

Вземи две прости вълни с различни честоти f₁ и f₂ при пробната честота f_s и с начална фаза равна на нула. Това са вълните sin(2π f₁ k / f_s) и sin(2π f₂ k / f_s). След n проби, тези вълни ще са съответно във фази -2π f₁ n / f_s и -2π f₂ k / f_s. Ако обозначим разликата във фазите с Δτ, тогава

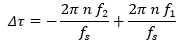
и

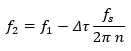
Така, можем да изчислим, че честотата на вълната, която се появява при 50 Hz, е всъщност

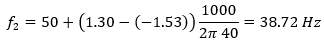
Това е доста близко до честотата на истинската вълна, която в този пример знаем, че е 40 Hz. Не е точно, но работата с дискретизирани данни никога не е точна.

Можем приблизително да изчислим честотите при всички други компоненти на DFT, като вземем разликата между фазата, която очакваме при всеки компонент в началото на втория DFT и фазата, която в действителност изчисляваме при второто DFT. Честотата 211 Hz ще бъде приблизителната оценка за 222 Hz при компонента на DFT при 250 Hz. Ще получим 460 Hz при компонента 475 Hz, като приблизителна оценка за 465 Hz.

Трябва да внимаваме винаги да вземем предвид броя на циклите, през които една проста вълна при един компонент може да е минала при дължината на един DFT, при изчисляването на очакваната фаза. При компонента 250 Hz на първия DFT например ще изчислим фазата -0.41 радиани. Една вълна от 250 Hz, при пробната честота 1000 Hz, ще мине през 10 цикъла преди да почне втория DFT. Така, очакваме, че фазата в началото на втория DFT ще бъде -63.24 радиани, но можем да нагласим тази фаза за 10 * 2π за да получим, пак, -0.41. Това е фазата, която трябва да очакваме в началото на втория DFT и която можем да сравним с фазата изчислена от второто DFT. На кратко, ако искаме да получим фази при първото и второто DFT, които можем да сравним, трябва да коригирам фазата, която очакваме в началото на второто DFT с по 2π докато разликата между тази очаквана фаза и действителната фаза във второто DFT е между –π и π.

Разбира се, ще получим честоти при всички компоненти на DFT, даже и при компоненти, които съвсем не са близо до действителните честоти. Тези са важни и трябва да се запазят, ако искаме да изградим сигнала правилно с обратното DFT.

Работа с части на сигнала

Някои от приблизителните преценки на истинските честоти ще изглеждат странни. При компонента на DFT 75 Hz например, ще изчислим честотата 119 Hz (със сравнително ниска амплитуда, разбира се). Интересно е, че тази 119 Hz се показва в този компонент. Очаквахме, че една такава честота ще се появи в компонента 100 Hz или в компонента 125 Hz. Това може да е нормално. Всяка проста честота ще се появи с някаква амплитуда, даже и ако е доста малка, във всички компоненти на DFT.

Можем да продължим с DFT при всяка следваща част от сигнала – при всеки 40 проби и можем да транспонираме честотите, които получаваме. Ако например искаме да транспонираме сигнала с един полутон нагоре, ще умножим записаните честоти по 2^1/12 – една равномерна октава се състои от дванадесет равно разпределени полутона и една октава нагоре означава удвояване на честотите.

След като свършим с транспонирането, можем да започнем да изграждаме транспонирания сигнал. Изчисляваме промяната във фазата за новите истински честоти, прикачваме ги към подходящите компоненти като използваме оригиналната им амплитуда и прилагаме обратното DFT. Тук обаче имаме проблем. На границата на всеки интервал от 40 проби, могат да се получат прекъсвания.

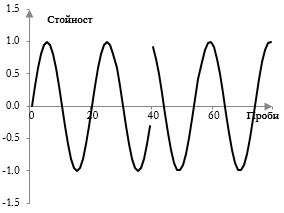
Едно прекъсване, като това показано в графиката по-долу, най-вероятно ще произведе доловимо пукане в сигнала. Най-добрия начин да се избягнат прекъсванията е cross-fading, смесването на края на първата част с началото на втората част, като плавно намаляваме амплитудата на първата част и увеличаваме амплитудата на втората част. Една проста такава операция е показана в следващата графика, където прекъснатите линии са амплитудите, приложени към всяка от двете части. За да направим това обаче ни трябват части, които се застъпват.

x

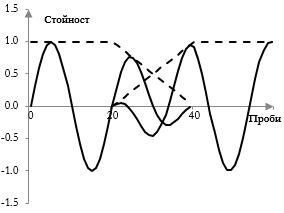
За да създадем едно транспониране, което работи, трябва да приложим DFT на застъпващи се части на сигнала. Ако самото DFT използва 40 точки, тогава второто може да започва не на проба 40, а на проба 20, което прави застъпването равно на половината от преобразуването.

Застъпването също помага с преценката на истинските честоти. В уравнението от по-горе

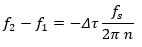
тъй като пазим –π  Δτ  π, тогава

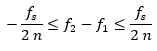
Ако размера на DFT е N, тогава

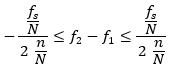
Всеки компонент на DFT тогава "отговаря" за f_s / N честоти. Когато n / N = 1 / 2 – компонентите на DFT се застъпват наполовина – тогава

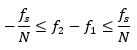
и сме сигурни, че приблизителната преценка на честота не прескача към друг компонент на DFT. Ако използваме застъпване от 20 точки в примера по-горе например – половината от 40 точки – вместо да изчислим, че истинската честота при компонента 75 Hz е 119 Hz, ще получим 88 Hz, което е по-близо до компонента. Вместо 38.72 Hz при компонента 50 Hz, ще получим 39.41 Hz. Това е по-добра преценка на истинската честота в сложния сигнал, която е 40 Hz.

На кратко, едно добро транспониране може да се направи като: 1) вземем DFT от последователни части на сигнала, които се застъпват поне наполовина; 2) отбележим амплитудата и разликата между очакваната фаза и действителната фаза изчислена в началото на всеки DFT (с изключение на първия) и изчислим истинската честота за всеки компонент на DFT; 3) изчислим преценените честоти за промяната в тоналността; 4) изчислим новите стойности на фазата и обратното DFT; и 5) изградим сигнала от обратното DFT с cross fading за застъпването.

Същият алгоритъм може да се приложи за разтягането или скъсяването на сигнала във времето, ако целта е да се промени неговото темпо без да се транспонира. Единствената разлика е, че вместо да променяме честотите на частите за тоналността, ще променим тяхното време преди обратното DFT.