Филтърът на Чебишев от втори вид се дава от нормализираната трансферна функция
$$H(S)=\epsilon \prod_{k=1}^{n} (S-r_k) \prod_{k=1}^{n} \frac{1}{S-s_k}$$
където n е разряда на филтъра, ε определя размера на вълните в амплитудния спектър на филтъра в лентата на спиране, корените на числителя rk са
$$r_k=\frac{1}{-j \, \cos(\frac{\pi (2k-1)}{2n})}$$
и корените на знаменателя sk са
$$s_k=\frac{1}{-\sinh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{n}) \, \sin(\frac{\pi (2k-1)}{2n})+j\,\cosh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{n}) \, \cos(\frac{\pi (2k-1)}{2n})}$$
Тук sinh и cosh са функциите за хиперболичните синус и косинус и asinh и acosh са обратните хиперболични синус и косинус.
Трансферната функция по-горе е показана независимо от преходната честота (т.е., тя е нормализирана за преходната честота 1) и различните форми на филтъра на Чебишев от втори вид изискват заместване. Трансферната функция тогава се нарича "нормализирана". Използвай S = s / ωc за да получиш нискочестотния филтър на Чебишев от втори вид, където s = jω, ωc е преходната честота на филтъра и ω е ъгловата честота в честотния диапазон между 0 и π. Използвай S = ωc / s за да получиш високочестотния филтър на Чебишев от втори вид. Използвай S = (s2 + ωc2) / (B s) за да получиш филтъра на Чебишев от втори вид, който пропуска някаква честотна лента (средночестотен), където ωc е средата на тази честотна лента и B е ширината на лентата. Използвай S = B s / (s2 + ωc2) за да получиш филтъра на Чебишев от втори вид, който спира някаква честотна лента (режекторен).
Този филтър също се нарича "обратен филтър на Чебишев". Корените на неговия знаменател са обратните корени на филтъра на Чебишев от първи вид и неговата амплитудна функция (показана по-долу) "обръща" амплитудната функция на филтъра на Чебишев от първи вид. Филтърът на Чебишев от първи вид контролира размера на вълните в лентата на пропускане, а този филтър има плоска лента на пропускане и контролира размера на вълните в лентата на спиране.
Пример: Нискочестотен филтър на Чебишев от втори вид и четвърти разряд
Заместваме n = 4 и S = s / ωc. Трансферната функция на нискочестотния филтър на Чебишев от втори вид и четвърти разряд е
$$H(s)=\frac{\epsilon (s-r_1\omega_c) (s-r_2\omega_c) (s-r_3\omega_c) (s-r_4\omega_c)}{(s-s_1\omega_c) (s-s_2\omega_c) (s-s_3\omega_c) (s-s_4\omega_c)}$$
Забележи, че r1 и r4 са спрегнати комплексни числа, r2 и r3 са спрегнати комплексни числа, s1 и s4 са спрегнати комплексни числа и s2 и s3 са спрегнати комплексни числа. Също така забележи, че реалните части на корените на числителя rk са нула и следователно r1 + r4 = 0 и r3 + r2 = 0. За да направим нашите изчисления по-лесни, изписваме трансферната функция по следния начин.
$$H(s)=\frac{\epsilon (s^2+r_1 r_4 \omega_c^2) (s^2+r_2 r_3 \omega_c^2)}{(s^2-(s_1+s_4)\omega_c+s_1 s_4 \omega_c^2)(s^2-(s_2+s_3)\omega_c+s_2 s_3 \omega_c^2)}$$
или
$$H(s)=\frac{\epsilon (s^4+A s^2 + B)}{s^4+C s^3+D s^2+E s + F}$$ $$A=\omega_c^2 (r_1 r_4 + r_2 r_3)$$ $$B=\omega_c^4 r_1 r_4 r_2 r_3$$ $$C=-\omega_c (s_1+s_4+s_2+s_3)$$ $$D=\omega_c^2 (s_1 s_4+s_2 s_3+(s_1 + s_4)(s_2+s_3))$$ $$E=-\omega_c^3 (s_1 s_4 (s_2+s_3) +s_2 s_3 (s_1 + s_4))$$ $$F=\omega_c^4 s_1 s_4 s_2 s_3$$
След билинейното преобразуване s = 2 (z – 1) / (z + 1) трансферната функция става трансферна функция с преобразуването Z.
$$H(z)=\frac{a_0+a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}+a_4 z^{-4}}{b_0+b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}+b_4 z^{-4}}$$ $$a_0=a_4=\epsilon (16+4 A+B)$$ $$a_1=a_3=\epsilon (-64+4B)$$ $$a_2=\epsilon (96-8A+6B)$$ $$b_0=16+8C+4D+2E+F$$ $$b_1=-64-16C+4E+4F$$ $$b_2=96-8D+6F$$ $$b_3=-64+16C-4E+4F$$ $$b_4=16-8C+4D-2E+F$$
Да предположим, че преходната честота на филтъра е ωc = 0.6 и че ε = 0.1 (по принцип, преходната честота на филтъра ще е ωc = 2 arctan(0.6/2) ≈ 0.583, заради изкривяването на честотния диапазон от билинейното преобразуване). Трансферната функция на този примерен нискочестотен филтър на Чебишев, след като умножим числителя и знаменателя по една и съща скаларна величина за да получим b0 = 1, е
$$H(z)=\frac{0.090729-0.190160z^{-1}+0.251568z^{-2}-0.190160z^{-3}+0.090729z^{-4}}{1-2.662409z^{-1}+2.828952z^{-2}-1.378102z^{-3}+0.264003z^{-4}}$$
и самият филтър е
$$y(k) = 0.090729 x(k) – 0.190160 x(k – 1) + 0.251568 x(k – 2)$$ $$– 0.190160 x(k – 3) + 0.090729 x(k – 4) + 2.662409 y(k – 1) $$ $$– 2.828952 y(k-2) + 1.378102 y(k – 3) – 0.264003 y(k – 4)$$
Ако пробната честота е например 2000 Hz, тогава преходната честота е ωc = (0.6 * 2000) / (2π) = 191 Hz. Амплитудният спектър на филтъра е показан в графиката по-долу.
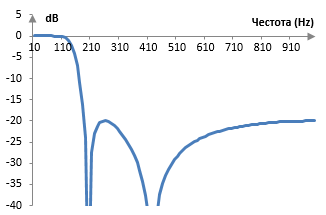
Размер на вълните в лентата на спиране
Функцията за амплитудата на нискочестотния филтър на Чебишев от втори вид може да се изпише като
$$|H(j\omega)|=\frac{1}{\sqrt{1+\frac{1}{\epsilon^2 T_n^2 (\frac{\omega_c}{\omega})}}}$$
където Tn са полиномите на Чебишев
$$T_n(x)=\begin{cases} \cos(n\,\mathrm{acos}(x)) & |x|\le1 \\ \cosh(n\, \mathrm{acosh}(x)) & |x| \gt 1 \end{cases}$$
В лентата на спиране, където ωc / ω < 1, Tn(ωc / ω) = \cos(n \mathrm{acos}(ωc / ω)) и 0 ≤ Tn2(ωc / ω) ≤ 1. В лентата на спиране
$$0 \lt |H(j\omega)| \le \frac{1}{\sqrt{1+\frac{1}{\epsilon^2}}}$$
Така, по-малките ε дават по-малки вълни в лентата на спиране и по-големите ε дават по-големи вълни. Можем също така да очакваме, че |H(jω)| клони към 0 когато ωc / ω клони към cos(π / 2n), защото тогава Tn(ωc / ω) = 0.
Със същите параметри както по-горе, n = 2 и ωc = 0.6, можем да покажем |H(jω)| за три различни стойности на ε (0.1, 0.2 и 0.3).
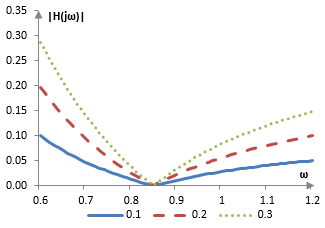
Амплитудните спектри на съответните филтри са:
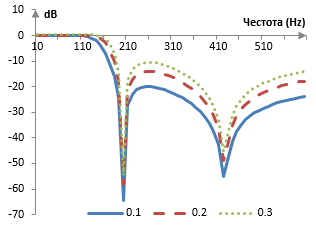
По-големите ε дават филтри с по-тясна преходна лента, но с по-големи вълни и по-лошо понижаване на амплитудата в лентата на спиране. По-малките ε създават филтри с по-малки вълни и по-добро понижаване на амплитудата в лентата на спиране, но с по-широки преходни ленти.
Пример: Филтър на Чебишев от втори вид и втори разряд за спиране на честотна лента
Използваме n = 2 и S = B s / (s2 + ωc2). Трансферната функция на филтъра на Чебишев от втори вид и втори разряд за спирането на някаква честотна лента е
$$H(s)=\epsilon \frac{B^2 s^2+r_1 r_2(s^2+\omega_c^2)^2}{B^2 s^2-B(s_1+s_2)(s^2+\omega_c^2)s+s_1 s_2(s^2+\omega_c^2)^2}$$
s1, s2, r1 и r2 се изчисляват със същите формули по-горе. След билинейното преобразуване s = 2 (z – 1) / (z + 1) ако вземем например ε = 0.1, B = 0.5 и ωc = 0.8 и след като умножим числителя и знаменателя по една и съща скаларна величина за да получим 1 в началото на знаменателя, ще получим следната трансферна функция.
$$H(z)= \frac{0.532250-1.506697z^{-1}+2.107234z^{-2}-1.506697z^{-3}+0.532250z^{-4}}{1+1.933150z^{-1}-1.879211z^{-2}+1.065289z^{-3}-0.276782z^{-4}}$$
Ако предположим, че пробната честота е 2000 Hz, тогава ωc = (0.8 * 2000) / (2 π) = 255 Hz, B = (0.5 * 2000) / (2 π) = 159 Hz и амплитудният спектър на филтъра е следния.
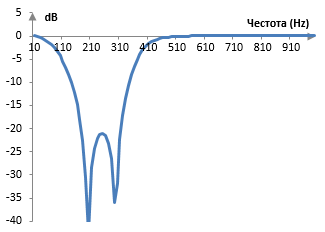
Филтри на Чебишев от по-високи разряди
Филтри на Чебишев от по-високи разряди могат да бъдат създадени с методите по-горе или като се подредят няколко филтъра от по-нисък разряд един след друг. Трансферната функция на нискочестотния филтър на Чебишев от втори вид и четвърти разряд например може да се изпише по следния начин.
$$H(s)= \epsilon \frac{(s-r_1\omega_c)(s-r_4\omega_c)}{(s-s_1\omega_c)(s-s_4\omega_c)} \frac{(s-r_2\omega_c)(s-r_3\omega_c)}{(s-s_2\omega_c)(s-s_3\omega_c)}$$
Това означава, че филтъра на Чебишев от втори вид и четвърти разряд може да се създаде, като се подредят два филтъра от втори разряд (това не са филтри на Чебишев от втори вид, защото техните корени не са корените на Чебишев). Умножаването на две трансферни функции означава, че импулсният спектър на целия филтър е конволюцията на двата импулсни спектъра на филтрите от по-нисък разряд и че изходният сигнал от първия филтър е входния сигнал във втория филтър. Корените са комбинирани по начина показан по-горе, защото s1 и s4, s2 и s3, r1 и r4 и r2 и r3 са комплексни спрегнати двойки. Не е важно дали ε се използва в първия филтър, във втория филтър или пък е разделено между двата филтъра.
Следната графика сравнява амплитудните спектри на нискочестотните филтри на Чебишев от втори вид от втори и четвърти разряд с ε = 0.1, пробна честота 2000 Hz и ωc = 0.6.
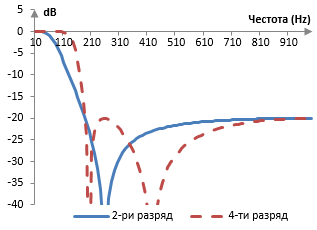
Филтри на Чебишев от втори вид и нечетен разряд
Когато филтърът на Чебишев от втори вид е от нечетен разряд, един от корените на числителя не може да бъде изчислен, защото произвежда деление на нула. При k = (n – 1) / 2 имаме rk = 1 / (-j cos(π / 2)). Така, когато n е нечетно, средният корен на числителя се маха от трансферната функция и числителя става полином от степен, която е по-ниска от степента на знаменателя. Вземи например нискочестотния филтър на Чебишев от втори вид и с разряд n = 3. Трансферната му функция, след като махнем средния корен r2, е следната.
$$H(s)= \epsilon \frac{(s-r_1\omega_c)(s-r_3\omega_c)}{(s-s_1\omega_c)(s-s_2\omega_c)(s-s_3\omega_c)}$$
Тъй като r1 и r3 са комплексни спрегнати числа, s1 и s3 са комплексни спрегнати и s2 е реално число, можем да изпишем трансферната функция по-горе като функция с реални коефициенти по следния начин.
$$H(s)= \frac{\epsilon (s^2+r_1 r_3 \omega_c^2)}{s^3-(s_1+s_3+s_2)\omega_c s^2+(s_1 s_3+(s_1+s_3)s_2)\omega_c^2 s-s_1 s_3 s_2 \omega_c^3}$$
След билинейното преобразуване този филтър има трансферната функция
$$H(z)= \frac{a_0+a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}}{b_0+b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}}$$ $$a_0=a_3=\epsilon(4+r_1 r_3 \omega_c^2)$$ $$a_1=a_2=\epsilon(-4+3 r_1 r_3 \omega_c^2)$$ $$b_0=8-4(s_1+s_3+s_2)\omega_c+2(s_1 s_3+(s_1+s_3)s_2)\omega_c^2-s_1 s_3 s_2\omega_c^3$$ $$b_1=-24+4(s_1+s_3+s_2)\omega_c+2(s_1 s_3+(s_1+s_3)s_2)\omega_c^2-3 s_1 s_3 s_2\omega_c^3$$ $$b_2=24+4(s_1+s_3+s_2)\omega_c-2(s_1 s_3+(s_1+s_3)s_2)\omega_c^2-3 s_1 s_3 s_2\omega_c^3$$ $$b_3=-8-4(s_1+s_3+s_2)\omega_c-2(s_1 s_3+(s_1+s_3)s_2)\omega_c^2-s_1 s_3 s_2\omega_c^3$$
Когато ωc = 0.6 например и след като умножим числителя и знаменателя по една и съща скаларна величина за да получим b0 = 1, филтърът става
$$H(z)=\frac{0.0369-0.0211z^{-1}-0.0211z^{-2}+0.0369z^{-3}}{1-2.179z^{-1}+1.666z^{-2}-0.431z^{-3}}$$
Този филтър обаче дава амплитуден спектър в лентата на пропускане от около -5 dB. За да създадем един филтър, който не понижава амплитудата в лентата на пропускане, умножаваме коефициентите в числителя така, че функцията H(s) да е равна на 1 при нула. Тоест, умножаваме по
$$\frac{1}{|H(0)|}=\frac{s_1 s_3 s_2 \omega_c^3}{\epsilon r_1 r_3 \omega_c^2}$$
Тази допълнителна амплитуда за филтъра в примера по-горе е 1.8 и самият филтър става
$$H(z)=\frac{0.0665-0.0380z^{-1}-0.0380z^{-2}+0.0665z^{-3}}{1-2.179z^{-1}+1.666z^{-2}-0.431z^{-3}}$$
Амплитудния спектър на този филтър от трети разряд е показан по-долу с амплитудните спектри на филтрите на Чебишев от втори вид и от втори и четвърти разряд.
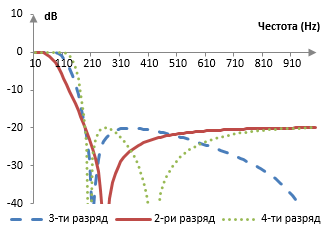
Добави нов коментар