Коефициентите a(k) на прозореца на Долф и Чебишев са следните.
$$a(k)=\frac{1}{N} \sum_{n=0}^{M} \frac{T_{2M}(\frac{\cos(\omega_n / 2)}{\cos(\omega_0 / 2)})}{T_{2M}(\frac{1}{\cos(\omega_0 / 2)})}\, \cos((k-M)\omega_n)$$
където N е дължината на прозореца; M = (N – 1) / 2; k = 0, 1, …, N; ωn = n π / (N – 1), ω0 е константа (ω0 > 0), T2M са полиномите на Чебишев
$$T_{2M}(x)=\begin{cases} \cos(2\,M\, \mathrm{acos}(x)), & |x|\le1 \\ \cosh(2\,M\, \mathrm{acosh}(x)), & |x|\gt1
\end{cases}$$
и cosh и acosh са хиперболичния косинус и арккосинус
$$\cosh(x)=\frac{1}{2} (e^x+e^{-x})$$ $$\mathrm{acosh}(x)=ln(x+\sqrt{x^2-1}), \,x\ge1$$
Забележи, че върхът на този прозорец не е равен на 1, но прозорецът може да бъде нормализиран, така че върхът му да е 1.
$$a(k)=\frac{a(k)}{a(M)}$$
Терминът 1 / N преди сумата в първата формула по-горе не е нужен, не е там за да направи формулата по-близка до обратното дискретизирано преобразуване на Фурие, както е обяснено по-долу.
Стойностите на ω0 обикновено са малки (< 0.1; въпреки че примерите по-долу използват по-големи стойности заради проблеми с прецизността). Други определения на прозореца на Долф и Чебишев използват
$$\frac{1}{\cos(\frac{\omega_0}{2})}=\cosh(\frac{1}{N} \, \mathrm{acosh}(10^\alpha))$$
Тук, константата α > 0 дава 1 / \cos(ω0 / 2) ≥ 1 и 1 / \cos(ω0 / 2) приблизително равно на 1. Това създава един прозорец на Долф и Чебишев, главният лоб (на прозореца, не на филтъра) на който е сравнително широк и страните на който – тези, които потискат страничните лобове на филтъра – са сравнително къси. Това е същото, както когато се използват стойности за ω0, които са близко до нула.
Мотивация за прозореца на Долф и Чебишев
Вземи функцията
$$H(\omega)=\frac{T_{2M}(\frac{\cos(\omega / 2)}{\cos(\omega_0 / 2)})}{T_{2M}(\frac{1}{\cos(\omega_0 / 2)})}$$
Когато ω минава между 0 и ω0, H намалява от 1 до 1 / T2M (1 / cos(ω0 / 2)). Когато ω продължава между ω0 и π, H се движи между 1 / T2M (1 / cos(ω0 / 2)) и -1 / T2M (1 / cos(ω0 / 2)). За перспектива, при ω0 = 1 и M = 100, T2M (1 / cos(ω0 / 2)) = 1.15E+45 и 1 / T2M (1 / cos(ω0 / 2)) = 8.71E-46. При тези параметри, функцията е тази показана в графиката по-долу.
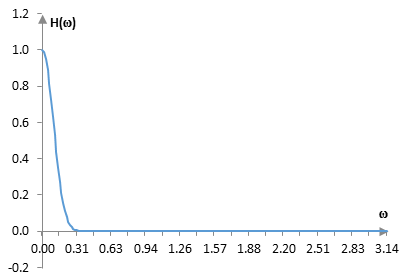
От една страна, тази функция може да е един реалистичен амплитуден спектър на един нискочестотен филтър, въпреки че намалява доста бързо. Въпреки че е трудно да се види в графиката, ω0 е честотата, при която амплитудният спектър H(ω) на прозореца на Долф и Чебишев стига своята "лента на спиране". За да изчислим филтъра на Долф и Чебишев от тази функция, можем да вземем обратното преобразуване на Фурие (с огледалната си част и изместен за да е с център при M, а не при 0). Това дава функцията показана най-горе в тази тема.
От друга страна, тази функция наподобява един импулс. Тъй като преобразуването на Фурие на произведението на две функции (филтъра и прозореца) е конволюцията на две преобразувания на Фурие (преобразуването на филтъра и преобразуването на прозореца), преобразуването на Фурие на прозореца е като филтър върху преобразуването на Фурие на филтъра. С други думи, амплитудният спектър на прозореца (в графиката по-горе) действа като филтър върху амплитудния спектър на филтъра, върху прозорецът е приложен.
Колкото по-малка е стойността на ω0 в прозореца на Долф и Чебишев, толкова повече функцията наподобява един импулс и действа подобно на един всичкопропускащ филтър върху амплитудния спектър на един филтър с ограничен импулсен спектър. Амплитудният спектър на филтъра остава непроменен, като при прилагането на един правоъгълен прозорец. С по-малки ω0, прозореца на Долф и Чебишев наподобява повече правоъгълния прозорец. С по-големи ω0, лобът на амплитудния спектър в графиката по-горе става по-голям и прозорецът на Долф и Чебишев създава по-гладък амплитуден спектър на филтъра.
Примери на прозореца на Долф и Чебишев
Следното е прозореца на Долф и Чебишев при три различни стойности на ω0 (0.1, 0.2 и 0.3) с N = 201 и M = 100.
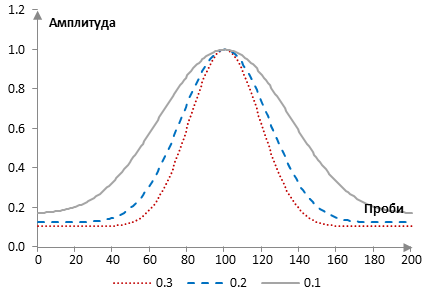
Да предположим, че пробната честота е 2000 Hz. Вземи един нискочестотен филтър с преходна честота 40 Hz. Амплитудните спектри на съответните три филтри са показани в следната графика.
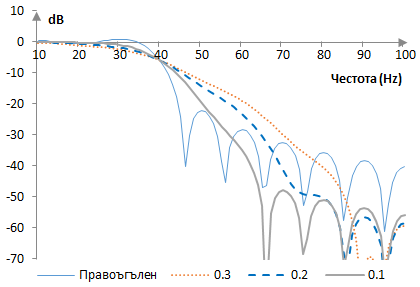
Когато ω0 се увеличава, прозорецът на Долф и Чебишев става по-тесен, атенюацията в лентата на спиране става по-добра, но преходната лента става по-широка.
Бележка за параметъра M
По принцип, при създаването на прозореца на Долф и Чебишев, няма нужда да се връзва параметъра M в полиномите на Чебишев T2M с дължината на прозореца N в обратното преобразуване на Фурие (във формулата по-горе M = (N – 1) / 2). Можем да изпишем формулата за прозореца на Долф и Чебишев по следния начин.
$$a(k)=\frac{1}{N} \sum_{n=0}^{M} \frac{T_{2L}(\frac{\cos(\omega_n / 2)}{\cos(\omega_0 / 2)})}{T_{2L}(\frac{1}{\cos(\omega_0 / 2)})}\, \cos((k-M)\omega_n)$$
където между N и L няма връзка. Следното е прозорецът на Долф и Чебишев от предишния пример с ω0 = 0.2 и с L = 100 и L = 75.
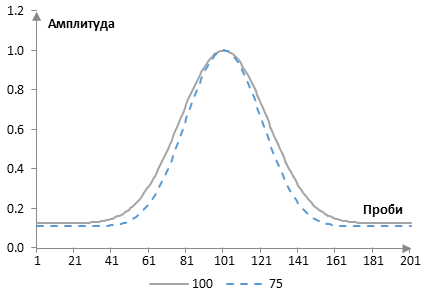
Амплитудните спектри на съответните филтри с дължина 201 и с преходна честота 40 Hz са следните.
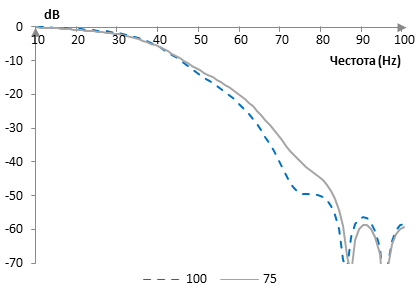
Ако всичко останало е непроменено, едно по-голямо L ще произведе един прозорец на Долф и Чебишев с по-широк лоб и съответен филтър с по-добра атенюация в лентата на спиране, но с по-широка преходна лента.
Измерения за прозореца на Долф и Чебишев
Следното е графика на дискретизираното преобразуване на Фурие на прозореца на Долф и Чебишев върху дискретизираното преобразуване на Фурие на правоъгълния прозорец (с ω0 = 0.1).
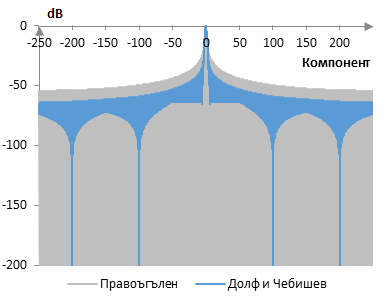
Измеренията на прозореца на Долф и Чебишев са следните.
| ω0 = 0.1 | ω0 = 0.2 | ω0 = 0.3 | |
| Кохерентна амплитуда | 0.34 | 0.25 | 0.20 |
| Еквивалентна лента на шума | 1.80 | 2.33 | 2.72 |
| Загуба при преработката | -2.56 dB | -3.66 dB | -4.35 dB |
| Загуба на лоба | -1.44 dB | -1.28 dB | -1.23 dB |
| Загуба при преработката в най-лошия случай | -4.00 dB | -4.94 dB | -5.58 dB |
| Ниво на най-високия страничен лоб | -29.6 dB | -31.9 dB | -35.1 dB1 |
| Спадане на страничните лобове | -7.1 dB / октава, -23.5 dB / декада | -7.1 dB / октава, -23.5 dB / декада | -7.1 dB / октава, -23.5 dB / декада |
| Главният лоб е -3 dB | 1.46 компонента | 1.58 компонента | 1.64 компонента |
| Главният лоб е -6 dB | 2.18 компонента | 2.58 компонента | 3.48 компонента |
| Корелация при застъпването при застъпване от 50% | 0.155 | 0.120 | 0.102 |
| Амплитудна гладкост при застъпване от 50% | 0.272 | 0.154 | 0.127 |
| Корелация при застъпването при застъпване от 75% | 0.440 | 0.261 | 0.201 |
| Амплитудна гладкост при застъпване от 75% | 0.914 | 0.579 | 0.377 |
1 Когато ω0 се увеличава, страничните лобове, които са най-близо до главния лоб на прозореца на Долф и Чебишев, изчезват бавно. Тези нива на най-високия страничен лоб не са прецизни, защото може да има странични лобове, които са по-близо до главния лоб и още не са изгладени.
Виж също:
Прозорец
Добави нов коментар