Преобразуване на Фурие

Съществуват определения за три различни преобразувания на Фурие. Всичките имат приложения при работата с цифрови сигнали.

Преобразуването на Фурие на функцията x(t) се дава от формулата

$$H(s)=\int_{-\infty}^{\infty} x(t) \, e^{-2\pi\,j\,t\,s} \, dt$$

Обратното преобразуване на Фурие е

$$x(t)=\int_{-\infty}^{\infty} H(s) \, e^{2\pi\,j\,t\,s} \, ds$$

Дискретизираното преобразуване на Фурие на функцията x(k) се дава от формулата

$$H(n)=\sum_{k=0}^{N-1} x(k) \, e^{-\frac{2\pi\,j\,k\,n}{N}}, \, n=0,1,...,N-1$$

и съответното обратно преобразуване е

$$x(k)=\frac{1}{N}\sum_{n=0}^{N-1} H(n) \, e^{\frac{2\pi\,j\,k\,n}{N}}, \, k=0,1,...,N-1$$

Преобразуването на Фурие в дискретизирано време се дава от формулата

$$H(s)=\sum_{k=-\infty}^{\infty} x(k) \, e^{-2\pi\,s\,j\,k}$$

и съответното обратно преобразуване, обикновено описано с ω = 2π f, е

$$x(k)=\frac{1}{2\pi}\int_{-\pi}^{\pi} H(\omega) \, e^{j\,\omega\,k} \, d\omega$$

За тези три преобразувания понякога се използват съкращенията FT, DFT и DTFT (от англ., "Fourier transform", "discrete Fourier transform" и "discrete-time Fourier transform").

Интерпретация на преобразуването на Фурие

Както всяко друго преобразувания, преобразуването на Фурие превежда един вид функции в друг. При работата с цифрови сигнали, типичното тълкуване на преобразуването на Фурие е, че преобразуването на Фурие превежда един сигнал – една функция на времето и със стойности стойностите на сигнала при дадени амплитуди, честоти и фази – в една функция на честотите, стойностите на която дават амплитудите и фазите на тези честоти в дадено време.

Обикновено, определяме сигнала x(t) като една сума на прости синусоиди като например следното.

$$x(t)=\sum_{n=0}^{N-1} A_n \, \cos(2\pi\,f_n\,(t-\tau_n))$$

където f_n, A_n и τ_n са съответно честотите, амплитудите и фазите на простите вълни. Сигналът x(t) е функция на времето за един комплект предопределени честоти, амплитуди и фази. Стойностите на x(t) са стойностите на сигнала.

Преобразуването на Фурие H(s) от друга страна е функция на честотите s. Самият H(s) има комплексни стойности, които, както е показано по-долу, съдържат информация за амплитудите и фазите на простите вълни в сигнала. Тъй като времето t не е част от аргумента или стойностите на H(s) преобразуването на Фурие H(s) произвежда амплитудите и фазите на честотата s за някакво предопределено време t. Преобразуването може да даде различни амплитуди и фази при различни времена t.

Един опростен начин да кажем това е, че ако имаме един сигнал като функция на времето, преобразуването на Фурие ще ни помогне да намерим и анализираме амплитудите и фазите на честотите, които са в сигнала.

Следното помага да покажем това при дискретизираното преобразуване на Фурие.

Вземи дискретизираното преобразуване на Фурие на един сигнал x(k) в дискретизираното време k и приложи формулата на Ойлер.

$$H(n)=\sum_{k=0}^{N-1} x(k) \, e^{-\frac{2\pi\,j\,k\,n}{N}}$$ $$=\sum_{k=0}^{N-1} x(k) \, \cos(\frac{2\pi\,k\,n}{N})-j \sum_{k=0}^{N-1} x(k) \, \sin(\frac{2\pi\,k\,n}{N})$$

за n = 0, 1, …, N – 1. Да предположим, че x(k) е един сигнал с реални стойности. Анализа на Фурие ни казва, че

$$\sum_{k=0}^{N-1} x(k) \, \cos(\frac{2\pi\,k\,n}{N}) \approx \frac{N B_n}{2}$$ $$\sum_{k=0}^{N-1} x(k) \, \sin(\frac{2\pi\,k\,n}{N}) \approx \frac{N C_n}{2}$$

където B_n = A_n cos(2π n τ_n) и C_n = A_n sin(2π n τ_n) са коефициентите на простата вълна A_n cos(2π n (t - τ_n)) в x(k) с честота цялото число n, амплитуда A_n и фаза τ_n.

Както е обяснено в темата Анализ на Фурие, горният резултат се получава, защото простите вълни са ортогонални и сумите по-горе са нула (приблизително в дискретизирания случай) за всички такива прости вълни в x(k) освен тези при n и при N – n.

$$H(n) \approx \frac{N\,B_n}{2}-j \frac{N\,C_n}{2}$$

И още,, B_n и C_n могат да се използват за да се изчислят амплитудата и фазата

$$|A_n|=\sqrt{B_n^2+C_n^2}$$ $$\Phi_n=\mathrm{atan2}(\frac{C_n}{B_n})$$

на честотата n в сигнала x(k).

Просто казано, H(n), n-тата комплексна стойност на преобразуването на Фурие, ни помага да намерим амплитудата A_n и фазата Φ_n (чрез коефициентите B_n и C_n) на простата вълна с честота цялото число n в сложния сигнал x(k).

На практика, често имаме само един сложен сигнал x(t) или x(k) и не знаем какви честоти съществуват в този сигнал. Можем да използваме преобразуването на Фурие за да ги намерим. В примера по-горе, преобразуването на Фурие разлага сложния сигнал със стойности равни на реални числа, стойностите на сигнала във времето, в един комплект от амплитуди и фази H(n) за честотите n.

На практика, също така няма и гаранция, че сложният сигнал x(t) или x(k) е съставен от прости синусоиди със честоти, които са цели числа (виж например Квадратна вълна). Често обаче можем приблизително да представим този сигнал като сума от такива вълни, както е обяснено в темата Анализ на Фурие.

Така, преобразуването на Фурие е едно естествено разширение на редовете на Фурие. Имаме три причини за използването на преобразуването на Фурие вместо редовете на Фурие. Първо, преобразуването на Фурие позволява по-кратки записи на изчисленията / уравненията. Второ, комплексните числа позволяват на преобразуването на Фурие да произведе една функция с комплексни стойности, което означава две различни стойности, които могат да се използват за амплитудата и фазата на сигнала. Комплексните числа ни позволяват едновременно да изчислим коефициентите B_n и C_n и да произведем една единствена функция H(n) – една функция, която ни дава (не директно) амплитудата и фазата. Трето, преобразуването на Фурие има обратно преобразуване, което може лесно да се изпише и което има своите употреби.

Пример – дискретизираното преобразуване на Фурие на една проста вълна

Вземи една проста дискретизирана вълна с честота f, амплитуда A и фаза m и с N проби за един период от време равен на 1. Стойностите на тази проста вълна ще са

$$A \, \sin(\frac{2\pi\,f\,(k-m)}{N})=B \, \cos(\frac{2\pi\,f\,k}{N})+C \, \sin(\frac{2\pi\,f\,k}{N})$$

където B = -A sin(2π f m / N) и C = A cos(2π f m / N). Можем да изчислим дискретизираното преобразуване на Фурие по следния начин.

$$H(n)=\sum_{k=0}^{N-1}(B \, \cos(\frac{2\pi\,f\,k}{N})+C \, \sin(\frac{2\pi\,f\,k}{N})) \, e^{-\frac{2\pi\,j\,k\,n}{N}}$$

за n = 0, 1, …, N – 1. Използваме пак формулата на Ойлер

$$e^{-\frac{2\pi\,j\,k\,n}{N}}=\cos(\frac{2\pi\,n\,k}{N})-j \, \sin(\frac{2\pi\,n\,k}{N})$$

и отбелязваме, че компонентите на преобразуването на Фурие (синусите и косинусите с честоти n) са ортогонални спрямо простата вълна с честота f в дадения интервал с изключение на два случая – при n = f и при н = N – f. Във втория случай имаме

$$\cos(\frac{2\pi\,n\,(N-k)}{N})=\cos(2\pi\,n-\frac{2\pi\,n\,k}{N})=\cos(\frac{2\pi\,n\,k}{N})$$ $$\sin(\frac{2\pi\,n\,(N-k)}{N})=\sin(2\pi\,n-\frac{2\pi\,n\,k}{N})=-\sin(\frac{2\pi\,n\,k}{N})$$

Преобразуването, като функция на n, е

$$H(n) \approx \begin{cases} B \sum_{k=0}^{N-1} \cos^2 (\frac{2\pi\,k\,n}{N}) - j \, C \sin^2 (\frac{2\pi\,k\,n}{N}), \, n=f, N-f \\ 0, \,\, n \ne f, N-f\end{cases}$$

Двете суми, при достатъчно голяма пробна честота N, са приблизително равни на N / 2 и следователно, преобразуването е просто

$$H(n) \approx \begin{cases} \frac{N}{2} (B - j \, C), \, n=f, N-f \\ 0, \,\, n \ne f, N-f\end{cases}$$

Така, дискретизираното преобразуване на Фурие на една проста вълна с честота f дава една функция H(n), която показва нещо за вълната при компоненти n = f и n = N – f и е нула в останалите случаи. По-точно, при n = f и n = N – f.

$$|H(n)| \approx \sqrt{Re(H(n))^2+Im(H(n))^2}=\frac{N}{2} \sqrt{B^2+C^2}=\frac{N}{2} A$$ $$\mathrm{atan2}(Im(H(n)),\,Re(H(n)))=\mathrm{atan2}(N C,\,N B)=-\frac{2\pi\,f\,m}{N}$$

Това са амплитудата (умножена по N / 2) и фазата на оригиналната проста вълна.

Пример – дискретизираното преобразуване на Фурие на един сложен сигнал със стойности равни на реални числа

Ако оригиналната вълна е един сложен сигнал със стойности равни на реални числа, състоящ се от много вълни с различни амплитуди и честоти, резултатът ще е подобен, защото синусите и косинусите с различни честоти са ортогонални. Всеки компонент на дискретизираното преобразуване на Фурие (за всяко n) ще произведе амплитудата и фазата на съответната проста вълна (с честота n) в сложния сигнал, ако тази вълна съществува в сложния сигнал.

Дискретизираното преобразуване на Фурие H(n) на сигнала с реални стойности x(k), с аргумент честотата n, показва амплитудата на n-товата проста вълна в сигнала x(k)

$$A_n=2 \frac{|H(n)|}{N}=2 \frac{\sqrt{Re(H(n))^2+Im(H(n))^2}}{N}$$

и фазата на n-товата вълна в x(k) е

$$\Phi_n=\mathrm{atan2}(Im(H(n),Re(H(n)))$$

Важно е да отбележим, че преобразуването на Фурие работи, защото неговите компоненти (базата на преобразуването), а и синусите и косинусите по принцип са ортогонални над правилно избрани интервали. В идеалния случай, когато един сигнал се състои само от вълни с честоти равни на тези, които се използват от преобразуването, интегралите или сумите в преобразуването ще дадат нула във всички случаи, освен когато вълната в сигнала е със същата честота като компонента в преобразуването. (В другите случаи, когато честотите на сигнала не са същите като тези на компонентите на преобразуването, резултатът е по-непрецизен, но подобен).

Излишни стойности на преобразуването на Фурие на един сигнал със стойности равни на реални числа

Да предположим, че изчисляваме дискретизираното преобразуване на Фурие за простата вълна с честота 10 Hz, като използваме дискретизираното преобразуване на Фурие със 100 точки над 2 секунди от вълната. Амплитудите на дискретизираните компоненти на преобразуването на Фурие ще бъдат както в графиката по-долу.

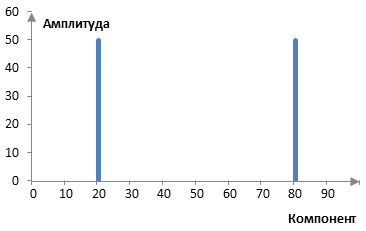
Дискретизираното преобразуване на Фурие не е нула – приблизително – при компоненти 20 и 80. Тъй като използваме 100 точки над 2 секунди, по принцип използваме пробната честота 50 Hz. Това означава, че използваме дискретизираното преобразуване на Фурие с компоненти 0.5 Hz, 1 Hz, 1.5 Hz, …, 49.5 Hz (Тези кратни на 0.5 Hz са ортогонални в интервала от 2 секунди.). 20-тият компонент е 10 Hz и е нормално да получим ненулева стойност за този компонент. Според дискусията по-горе, нормално е и да получим ненулева стойност за компонента 80 = 100 – 20. Амплитудите на дискретизираното преобразуване на Фурие при тези два компонента са 100 / 2 = 50. Резултатите са такива, каквито очаквахме. (Избрахме да изчислим дискретизираното преобразуване на Фурие с N равно разпределени точки над 2. Какви точки изберем за дискретизираното преобразуване на Фурие влияе на това, кои са неговите компоненти. Тук компонентите са честотите между 0 и N / 2. Дискретизираното преобразуване на Фурие най-често се изчислява с първите N на някакъв сигнал с пробната честота f_s. В този случай, компонентите са честотите 0, f_s / N, 2 f_s / N, …, (N – 1) f_s / N. Дискретизираното преобразуване на Фурие тогава поставя един интересен въпрос – какво означава компонента 0. Амплитудата на компонента при 0 на някакъв сигнал x(k) = A₀ + A₁ sin(2π k f / N) е N A₀. Така, въпреки че компонента 0 при дискретизираното преобразуване на Фурие на цифровите сигнали е безсмислен, при аналоговите сигнали той представлява силата на постоянния ток.)

Когато входния сигнал в дискретизираното преобразуване на Фурие или в обратното дискретизирано преобразуване на Фурие има реални, а не комплексни стойности, преобразуването произвежда такива комплексни числа, че H(N – 1 – n) е комплексно спрегнатото на H(n). Информацията за n > N / 2 е излишна.

Приблизителни стойности при дискретизираното преобразуването на Фурие

Забележи, че при примера за простата вълна от 10 Hz, един от компонентите на преобразуването на Фурие е 10 Hz. Това не се получава винаги. Един пример на графика, която ще се получи в други случаи – когато честотите в сигнала не съвпадат с компонентите на преобразуването – е показан в темата Анализ на Фурие.

Пример – дискретизираното преобразуване на Фурие при сигнали със стойности равни на комплексни числа

Фактът, че дискретизираното преобразуване на Фурие на един сигнал с реални стойности произвежда информация, която се повтаря и е излишна, притеснява. Имаме два избора. Първо, можем да пренебрегнем втората половина от резултатите от преобразуването. Второ, можем да дадем комплексни сигнали на преобразуването. Комплексната честота f с N проби например е

$$e^{-\frac{2\pi\,j\,f\,k}{N}}$$

Когато на дискретизираното преобразуване на Фурие се дават комплексни сигнали, обаче, резултатите са различни. Вземи простата вълна

$$e^{-\frac{2\pi\,j\,f\,k}{N}}=\cos(\frac{2\pi\,f\,k}{N})-j \, \sin(\frac{2\pi\,f\,k}{N})$$

Компонентът H(n) на дискретизираното преобразуване на Фурие при n = f ще бъде

$$H(n) = \sum_{n=0}^{N-1} (\cos^2(\frac{2\pi\,n\,k}{N}) + \, \sin^2(\frac{2\pi\,n\,k}{N}))$$ $$-j \, \sum_{n=0}^{N-1} (\sin(\frac{2\pi\,n\,k}{N}) \, \cos(\frac{2\pi\,n\,k}{N})+\sin(\frac{2\pi\,n\,k}{N}) \, \cos(\frac{2\pi\,n\,k}{N}))$$ $$=N$$

Този резултат е два пъти по-голям от резултата при дискретизираното преобразуване на Фурие на един сигнал с реални стойности.

Дискретизираното преобразуване на Фурие H(n) на един сигнал x(k) с комплексни стойности показва амплитудата на n-товата проста вълна в сигнала x(k)

$$A_n=\frac{|H(n)|}{N}=\frac{\sqrt{Re(H(n))^2+Im(H(n))^2}}{N}$$

и фазата на n-товата проста вълна в x(k)

$$\Phi_n=\mathrm{arg}(H(n))=\mathrm{atan2}(Im(H(n)),Re(H(n)))$$

Дискретизираното преобразуване на Фурие и филтрите с ограничени импулсни спектри

Един нискочестотен филтър с ограничен импулсен спектър е просто един сигнал, композиран от простите вълни с честоти, които са по-малки от преходната честота f_c (виж Нискочестотен филтър). Би трябвало да можем да използваме дискретизираното преобразуване на Фурие за да изчислим честотния спектър (амплитудния спектър и фазовия спектър) на нискочестотния филтър. Както по-горе, отбелязваме, че нискочестотният филтър има реални стойности и следователно можем да отхвърлим половината от компонентите. Отбелязваме и, че нискочестотният филтър с дължина N в темата Нискочестотен филтър вече е умножен по 2 / N. Така, ще използваме стандартното дискретизирано преобразуване на Фурие с N точки, но при изчисляването на амплитудата, няма да умножаваме по 2 / N. Изчислението за амплитудния спектър на филтъра ще бъде

$$|H(n)|=\sqrt{(\sum_{n=0}^{N-1} a(k) \, \sin(\frac{2\pi\,n\,k}{N}))^2+(\sum_{n=0}^{N-1} a(k) \, \cos(\frac{2\pi\,n\,k}{N}))^2}$$

Тъй като дискретизираното преобразуване на Фурие е изчислено с малък брой компоненти – дължината на филтъра – означава, че амплитудният спектър ще бъде рядък и разпръснат в честотния диапазон, както в по-долната графика. Да предположим, че имаме пробната честота f_s = 2000 Hz и създаваме един стандартен нискочестотен филтър с ограничен импулсен спектър с дължина N = 101 и с преходна честота f_c = 40 Hz. Амплитудният спектър в графиката по-долу използва преобразуване с N = 101 точки, което е и дължината на филтъра. Преходната честота е между компоненти 2 и 3, което, при пробната честота fs = 2000 Hz, е между 39.6 Hz и 59.4 Hz (101 проби в 2000 Hz означава 19.8 Hz за всеки компонент). Забележи също, че графиката използва само първите 50 компонента, което е половината от N.

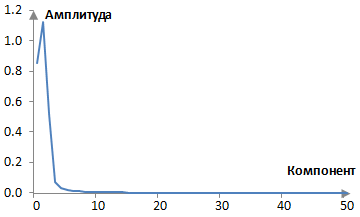
С дискретизираното преобразуване на Фурие можем и да изчислим фазовия спектър на нашия нискочестотен филтър. Отбелязваме, че филтърът има коефициенти, които са симетрични спрямо средата, т.е. a(k) = a(N – 1 – K). Да предположим засега, че Re(H(n)) > 0. Тогава

$$\Phi_n=\mathrm{atan2}(Im(H(n)),Re(H(n)))=\mathrm{atan}(\frac{Im(H(n))}{Re(H(n))})$$ $$=\mathrm{atan}(\frac{\sum_{n=0}^{N-1} a(k) \, \sin(\frac{2\pi\,n\,k}{N})}{\sum_{n=0}^{N-1} a(k) \, \cos(\frac{2\pi\,n\,k}{N})})$$

Тъй като a(k) = a(N – 1 – k),

$$a(k) \, \sin(\frac{2\pi\,k\,n}{N})+a(N-1-k) \, \sin(\frac{2\pi\,(N-1-k)\,n}{N})$$ $$=2 \, a(k) \, \sin(\frac{2\pi\,(N-1)\,n}{2N}) \, \cos(\frac{2\pi\,(N-1-2k)\,n}{2N})$$ $$a(k) \, \cos(\frac{2\pi\,k\,n}{N})+a(N-1-k) \, \cos(\frac{2\pi\,(N-1-k)\,n}{N})$$ $$=2 \, a(k) \, \cos(\frac{2\pi\,(N-1)\,n}{2N}) \, \cos(\frac{2\pi\,(N-1-2k)\,n}{2N})$$

Фазовият спектър, ако предположим, че филтърът е с нечетна дължина, е следния.

$$\Phi_n=\mathrm{atan}(\frac{2 \, \sin(\frac{2\pi\,n}{N} \frac{N-1}{2}) (1+\sum_{k=0}^{(N-1)/2} (a(k) \cos(\frac{2\pi\,n}{N} \frac{N-1-2k}{2})) )}{2 \, \cos(\frac{2\pi\,n}{N} \frac{N-1}{2}) (1+\sum_{k=0}^{(N-1)/2} (a(k) \cos(\frac{2\pi\,n}{N} \frac{N-1-2k}{2})) )})$$

"1 +" в числителя и знаменателя е там, ако филтърът е с нечетна дължина. Ако филтърът има четна дължина N, изчисленията ще бъдат същите, но без "1 +". Така,

$$\Phi_n=\mathrm{atan}(\frac{\sin(\frac{2\pi\,n}{N} \frac{N-1}{2})}{\cos(\frac{2\pi\,n}{N} \frac{N-1}{2}) })=\frac{2\pi\,n}{N} \frac{N-1}{2}$$

Фазовият спектър на един филтър с ограничен импулсен спектър и с коефициенти, които са симетрични спрямо средата, е линеен спрямо честотата n и дава забавяне от (N – 1) / 2 проби. В тези изчисления предположихме, че Re(H(n)) > 0, но и в другите случаи изчисленията са подобни.

Използване на обратното дискретизирано преобразуване на Фурие

Ако дискретизираното преобразуване на Фурие дава амплитудният спектър на филтъра, тогава би трябвало да можем да създадем един филтър като вземем обратното дискретизирано преобразуване на Фурие на някакъв желан амплитуден спектър. Темата Нискочестотен филтър показва, как можем да създадем един нискочестотен филтър, като съберем простите вълни с честоти до преходната честота.

$$a(k)=\frac{2}{f_s} \sum_{n=1}^{f_c} \cos(\frac{2\pi\,n\,k}{f_s}), \, k=0,1,...,f_s-1$$

където f_c е преходната честота и f_s е пробната честота. Това уравнение може да се изпише като

$$a(k)=2(\frac{1}{f_s} \sum_{n=1}^{f_s / 2} B_n \, \cos(\frac{2\pi\,n\,k}{f_s})), \, B_n=\begin{cases} 1, n \le f_c \\ 0, n \gt f_c\end{cases}$$

където B_n е желания амплитуден спектър на филтъра, равен на 1 до преходната честота f_c и на нула след това. Горната граница на сумата е f_s / 2 според Теоремата за дискретизацията.

Тази формула е подобна на обратното дискретизирано преобразуване на Фурие, с изключение на това, че използва само реалната част от комплексното обратно дискретизирано преобразуване на Фурие (затова само косинусите), е ограничена до половината от преобразуването (затова сумата е само до f_s / 2) и е умножена по 2. Така, тази формула използва проби с пробната честота в честотния диапазон и използва изчисления, подобни на обратното дискретизирано преобразуване на Фурие, за да създаде един филтър. Не е задължително да използваме проби само с пробната честота f_s и можем да използваме каквато и да е пробна честота N. С други думи, този нискочестотен филтър може да бъде създаден с

$$a(k)=2(\frac{1}{N} \sum_{n=1}^{N / 2} B_n \, \cos(\frac{2\pi\,n\,k}{N})), \, B_n=\begin{cases} 1, \frac{n\,f_s}{N} \le f_c \\ 0, \frac{n\,f_s}{N} \gt f_c\end{cases} , \, k=0,1,...,N-1$$

Знаем, че косинусите са симетрични спрямо нулата, и че филтърът a(k) би трябвало също да е симетричен спрямо нулата, ако искаме филтър с линеен фазов спектър. Можем да удължим сумата и да премахнем умножаването по 2 по следния начин.

$$a(k)=\frac{1}{N} \sum_{n=-N/2}^{N / 2} B_n \, \cos(\frac{2\pi\,n\,k}{N}), \, B_n=\begin{cases} 1, |\frac{n\,f_s}{N}| \le f_c \\ 0, |\frac{n\,f_s}{N}| \gt f_c\end{cases}$$

Забележи естественото добавяне на n = 0 към сумата. Тъй като B_{n представлява желания амплитуден спектър на филтъра, този амплитуден спектър би трябвало да остане равен на 1, когато честотата клони към нула.}

Накрая, ако искаме да направим филтъра симетричен спрямо (N – 1) / 2, можем да го изместим по следния начин.

$$a(k)=\frac{1}{N} \sum_{n=-N/2}^{N / 2} B_n \, \cos(\frac{2\pi\,n\,(k-\frac{N-1}{2})}{N}), \, B_n=\begin{cases} 1, |\frac{n\,f_s}{N}| \le f_c \\ 0, |\frac{n\,f_s}{N}| \gt f_c\end{cases}, \, k=0,1,...,N-1$$

Тази формула за филтъра наподобява обратното дискретизирано преобразуване на Фурие, но не е обратното дискретизирано преобразуване на Фурие. Няма да използваме обратното дискретизирано преобразуване на Фурие за да създадем един филтър с ограничен импулсен спектър. Между обратното преобразуване и изчислението на филтъра има важни разлики. Първо, формулата по-горе използва само реалната част на обратното дискретизирано преобразуване на Фурие. Второ, формулата по-горе е изместена и спрямо n, понеже сумата е от–N / 2 до N / 2, и спрямо k, защото сумата използва k – (N – 1) / 2.

Формулата по-горе е реалната част на обобщеното или изместено обратно дискретизирано комплексно преобразуване на Фурие, което обикновено се записва с

$$x(k)=\frac{1}{N} \sum_{k=0}^{N-1} H(n) \, e^{\frac{2\pi\,j\,(k+\alpha)\,(n+\beta)}{N}}$$

Забележи, че лесно можем да добавим имагинерната част на обратното дисретизирано преобразуване на Фурие по-горе. Понеже синусовите функции са нечетни (т.e., sin(-x) = -sin(x)), сумата от стойности на синусите за n = -N / 2, …, N / 2 ще бъде нула. С други думи, понеже избрахме желан амплитуден спектър B_n, който е симетричен спрямо нулата, създадохме едно обратно преобразуване, а и филтър, който съдържа само реални коефициенти.

Това, че използваме един желан амплитуден спектър, който включва отрицателни честоти, е може би неприятно, защото отрицателните честоти нямат кой знае колко смисъл. Техниката на използване на симетрични амплитудни спектри за да се получи филтър с реални коефициенти обаче се среща често.

Проби на (недискретизираното) обратното преобразуване на Фурие

Преобразуването на Фурие в непрекъснато (недискретизирано) време превежда един сигнал x(t), който е функция на времето за определени амплитуди, честоти и фази, в един сигнал H(x(t)), който е функция на честотите и фазите за определени амплитуди и време. Обратното преобразуване на Фурие превежда функции на честотите и фазите в сигнали във времето. Един пример на как могат да се вземат проби от обратното преобразуване на Фурие в непрекъснато време за да се получи един нискочестотен филтър е даден в темата Нискочестотен филтър.

Връзка между преобразуването на Фурие и други преобразувания

Преобразуването на Фурие в дискретизирано време е специален случай на преобразуването Z. То е преобразуването Z със z = e^jω = e^{j 2πf}.

Преобразуването на Фурие (недискретизирано) е еквивалентно на двустранното преобразуване на Лаплас със s = j ω = j 2πf.

Свойства на преобразуването на Фурие

Следното са някои от основните свойства на преобразуването на Фурие. Нека преобразуването на Фурие на x(t) да бъде H_s, както в определението в началото на тази тема. Ако имаме интегруемите функции x(t) и y(t), комплексните числа a и b, реални числа T и S и реалното ненулево число c

$$H(a\,x(t)+b\,y(t))=a\,H(x(t))+b\,H(y(t))$$ $$H(x(t-T))=e^{-j\,2\pi\,T\,s} H_s$$ $$H(e^{j\,2\pi\,t\,S}x(t)) = H_{s-S}$$ $$H(x(c\,t)) = \frac{1}{|c|} H_{s/c}$$ $$H(\overline{x(t)}) = \overline{H_{-s}}$$ $$H((x*y)(t)) = H(x(t)) \, H(y(t))$$

Първото свойство разбира се е линейността на преобразуването на Фурие. Второто и третото уравнение дават свойствата на времевото изместване. Четвъртото свойство е за мащаба във времевия диапазон. Петото уравнение показва свойствата на комплексното спрягане (което обяснява и излишните резултати, които се появяват при преобразуването реални данни). Последното уравнение показва преобразуването на конволюцията, което е полезно при създаването на трансферни функции на цифрови филтри, които са подредени един след друг.

Бележка за бързото преобразуване на Фурие

Изчисленията с дискретизираното преобразуване на Фурие са доста тежки. Всяко дискретизирано преобразуване на Фурие с дължина N използва N² умножения на комплексни числа. Това, че броят на изчисленията в дискретизираното преобразуване на Фурие е пропорционален на N², означава, че самото преобразуване се нарича O(N²) алгоритъм.

Като алтернатива може да се използва бързото преобразуване на Фурие или FFT (от англ., "fast Fourier transform" или "бързо преобразуване на Фурие"). FFT не е преобразуване, а е един алгоритъм за по-бързи изчисляване на дискретизираното преобразуване на Фурие. Съществуват доста на брой, достъпни и добри програмни реализации на FFT и няма да представим такива тук. Тук просто ще дадем теоретичната база на FFT, която е доста проста.

FFT използва следното уравнение, което е познато като лемата на Даниелсън и Ланцош. Дискретизираното преобразуване на Фурие с N точки H_N(x(k)), може да се запише по следния начин

$$H(n) = \sum_{k=0}^{N-1} x(k) \, e^{-\frac{2\pi\,j\,k\,n}{N}}$$ $$=\sum_{k=0}^{\frac{N}{2}-1} x(2k) \, e^{-\frac{2\pi\,2\,k\,n}{N}} + \sum_{k=0}^{\frac{N}{2}-1} x(2k+1) \, e^{-\frac{2\pi\,n\,(2k+1)}{N}}$$ $$=\sum_{k=0}^{\frac{N}{2}-1} x(2k) \, e^{-\frac{2\pi\,k\,n}{N/2}} + e^{-\frac{2\pi\,n}{N}} \sum_{k=0}^{\frac{N}{2}-1} x(2k+1) \, e^{-\frac{2\pi\,k\,n}{N/2}}$$ $$=H_{N/2}^{even}(x(k))+ e^{-\frac{2\pi\,k\,n}{N/2}} H_{N/2}^{odd} (x(k))$$

С други думи, дискретизираното преобразуване на Фурие с N точки може да се изчисли като сумата на две дискретизирани преобразувания на Фурие от по N / 2 точки, където първото преобразуване минава през четните компоненти на оригиналното преобразуване, а второто преобразуване минава през нечетните компоненти на оригиналното преобразуване. Второто преобразуване – с нечетните точки – трябва да се умножи с някаква константа.

Ако можем да разделим дискретизираното преобразуване на Фурие на две преобразувания с дължина N / 2, тогава можем и да разделим тези две нови преобразувания на четири преобразувания с дължина N / 4. Всъщност, ако изберем лесния случай, в който N е равно на 2 на някаква степен, можем да продължим да разделяме преобразуването на по-малки преобразувания, докато стигнем до няколко преобразувания с дължина 1.

При едно дискретизирано преобразуване на Фурие с дължина N, FFT ще използва N преобразувания с дължина едно и N комплексни изчисления заради константите, които се появяват пред преобразуванията с нечетна дължина. За FFT, обаче, ще трябват и log₂(N) изчисления за да се извърши разделянето на дискретизираното преобразуване на Фурие на по-малки преобразувания. Така, броят на операциите във FFT е пропорционален на N log₂(N), което означава, че FFT е един O(N log₂(N)) алгоритъм. При голям брой данни, FFT ще бъде доста по-бързо от дискретизираното преобразуване на Фурие. Дискретизираното преобразуване на Фурие може да се използва например при транспониране на аудио. При транспонирането на една аудио писта с дължина три минути може да трябват около 8 трилиона изчисления с дискретизираното преобразуване на Фурие, но за същото транспониране с FFT ще трябват само 80 милиона изчисления.