Коефициентите на прозореца на Хеминг се дават от формулата
$$w(k)=0.54-0.46 \, \cos(\frac{2\pi\,k}{N-1})$$
където N е дължината на филтъра и k = 0, 1, …, N – 1.
Един примерен прозорец на Хеминг
Вземи например един нискочестотен филтър с краен импулсен спектър (FIR) и с дължина N = 201. Следното е прозореца на Хеминг.
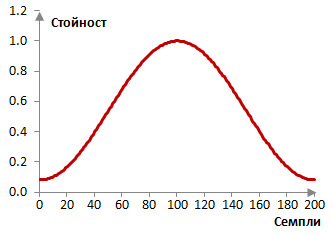
Ако пробната честота е 2000 Hz и преходната честота на филтъра е 40 Hz, тогава импулсният спектър на филтъра с правоъгълен прозорец (без прозорец) и с прозореца на Хеминг е както следва.
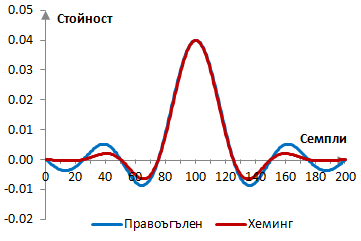
Амплитудният спектър на същия филтър е показан в графиката по-долу.
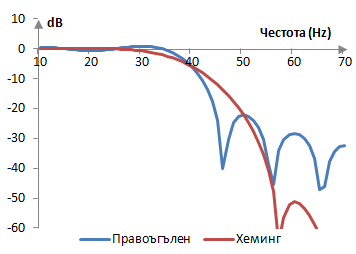
Извеждане на прозореца на Хеминг
Прозорците обикновено се използват за да смекчат вълните на феномена на Гибс, който е резултатът от използването на приближение с редовете на Фурие, редове от непрекъснати функции, върху един желан амплитуден спектър с прекъсване. За да намалим тези вълни, ще смекчим прекъсването. Вместо да създадем един филтър с обратното преобразуване на Фурие върху идеалния желан амплитуден спектър (в синьо по долу), ще използваме един нов амплитуден спектър (в червено).
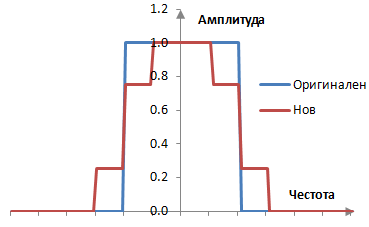
Разпознаваме този нов амплитуден спектър като сумата от оригиналния амплитуден спектър H, умножен по някаква скаларна величина, с две изместени негови версии, също умножени по някаква скаларна величина.
$$\alpha \, H(f)+\beta \, H(f-f_0)+\beta \, H(f+f_0)$$
където α е скаларната величина за оригиналния амплитуден спектър, β е скаларната величина на изместените амплитудни спектри и f0 и – f0 са двете измествания. В по-горния пример α = 0.5, β = 0.25 и f0 = ¼ fc, където fc е преходната честота.
Можем също така да отбележим, че филтърът след прозореца се получава, като филтърът се умножи по прозореца. Ако филтърът след прозореца беше създаден с обратното преобразуване на Фурие от някакъв желан амплитуден спектър, тогава желаният амплитуден спектър трябва да е конволюцията на преобразуването на Фурие на филтъра и преобразуването на Фурие на прозореца (по-точно, преобразуването на Фурие на две умножени функции е кръгова / периодична конволюция). Можем да запишем новия амплитуден спектър като една конволюция по следния начин.
$$H(f) * (\alpha \, \delta(f)+\beta \, \delta(f-f_0)+\beta \, \delta(f+f_0))$$
където δ е делта функцията на Дирак (използваме делта функцията на Дирак, защото ни позволява и да запишем желания амплитуден спектър като конволюция, и да разпознаем преобразуването на косинуса в последните две части). Обратното преобразуване на Фурие на този желан амплитуден спектър дава филтъра преди прозореца, умножен по прозореца
$$w(k)=\alpha+2\,\beta \frac{\cos(f_0 \, k)}{\pi}$$
Това е семейството прозорци на Хеминг, което включва самия прозорец на Хемин, а и прозореца на Хан. Този обобщен прозорец на Хеминг често се изписва по следния начин.
$$w(k)=\alpha-\beta \, \cos(\frac{2\pi\,k}{N-1})$$
Прозорците от семейството на Хеминг също са и "обобщение косинусови прозорци", които са прозорците от вида
$$w(k)=\sum_{m=0}^{M} a_m \, \cos(\frac{2\pi\,m\,k}{N-1})$$
M дава разряда на прозореца. Тук се включват прозореца на Блекмън, прозореца на Нътол, прозореца на Блекмън и Нътол, прозореца на Блекмън и Харис, прозорците на Райф и Винсънт и някои плоски прозорци. Правоъгълният прозорец също може да се счете за един обобщен косинусов прозорец (с разряд 0).
Измерения за прозореца на Хеминг
Дискретизираното преобразуване на Фурие на прозореца на Хеминг върху дискретизираното преобразуване на Фурие на правоъгълния прозорец е показано в следната графика.
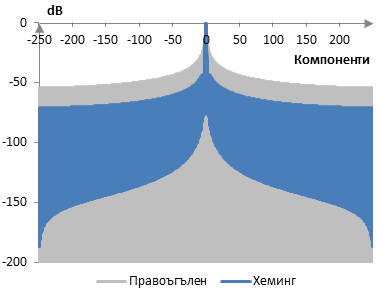
Измеренията за прозореца на Хеминг са следните.
| Кохерентна амплитуда | 0.54 |
| Еквивалентна лента на шума | 1.36 |
| Загуба при преработката | -1.35 dB |
| Загуба на лоба | -1.75 dB |
| Загуба при преработката в най-лошия случай | -3.10 dB |
| Ниво на най-високия страничен лоб | -44.4 dB |
| Спадане на страничните лобове | -7.9 dB / октава, -26.1 dB / декада |
| Главният лоб е -3 dB | 1.30 компонента |
| Главният лоб е -6 dB | 1.82 компонента |
| Корелация при застъпването при застъпване от 50% | 0.233 |
| Амплитудна гладкост при застъпване от 50% | 1.000 |
| Корелация при застъпването при застъпване от 75% | 0.706 |
| Амплитудна гладкост при застъпване от 75% | 1.000 |
Виж също:
Прозорец
Добави нов коментар