При работата със сигнали, импулсният спектър на оборудване или софтуер е графично, числово или математическо представяне на изходния сигнал (обикновено амплитудата на изходния сигнал) на това оборудване или софтуер след като към него е изпратен един импулс като входен сигнал.
Импулс
Един импулс е един сигнал, който е нула навсякъде освен в една определена точка във времето. С прости думи, един импулс е един мигновен пулс в един сигнал, който иначе е нула.
Когато един импулс се изпрати към една система – оборудване, софтуер и така нататък – ще се получи някакъв изходен сигнал. Изходният сигнал е импулсния спектър на системата.
Вземи например следния цифров сигнал.
…, 0, 0, …, 0, 1, 0, …, 0, 0, …
Този сигнал се състои от нули, с изключение на едно единствено 1 в една от пробите. Този сигнал е един импулс.
В математиката, делта функцията на Дирак ("функцията за единица импулс") е една функция, която е нула навсякъде освен при нула, където е безкрайно голяма. В дискретизирано време, делта функцията на Кронекер с аргументи две цели числа е нула навсякъде, освен когато двете цели числа са равни. И двете функции са примери на импулси.
Делта функцията на Кронекер също понякога се определя като една функция с един аргумент равен на цяло число и със стойности на функцията равни на нула навсякъде, освен в нулата, където функцията е равна на 1.
$$\delta(i)=\begin{cases}0, i \ne 0 \\ 1, i=0 \end{cases}$$
Делта функцията на Кронекер ще произведе примерния сигнал по-горе.
Импулсен спектър
Когато един импулс е входния сигнал в една система – оборудване, софтуер и така нататък – системата ще произведе някакъв изходен сигнал. Този изходен сигнал е импулсния спектър на системата.
В първия пример по-долу, когато един сигнал е изпратен през един прост дилей, дилея произвежда не само импулса, но и едно забавено и затихнало повторения на импулса. Това е целта на един дилей – един ефект DSP. Импулсният спектър е изходния сигнал, който се състои от импулса и от забавения и затихнал импулс.
Вторият пример по-долу е импулсния спектър на един усилвател с говорител за бас. Един усилвател за бас няма да възпроизведе сигнала перфектно, защото ще добави реверберациите от говорителя, някаква честотна окраска от усилвателя и говорителя и така нататък. Така, импулсния спектър на усилвателя не е просто един импулс, а е нещо по-сложно.
Пример: импулсен спектър на един прост дилей
Един прост дилей създава едно забавено и затихнало повторение на сигнала.
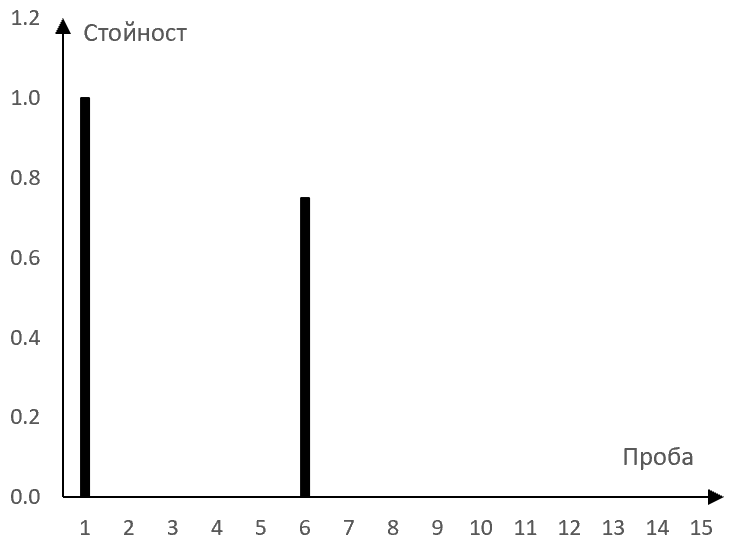
Ако например дилея повтори сигнала със забавяне от 5 проби и със 75% от неговата амплитуда, тогава дилея ще произведе следния изходен сигнал от импулса по-горе (оригиналният сигнал е включен).
…, 0, 0, …, 0, 1, 0, 0, 0, 0, 0.75, 0, …, 0, 0, …
Това е импулсния спектър на дилея. Представен в една графика, импулсният спектър ще е следния.
Работа с импулсния спектър
Можем да използваме импулсния спектър на простия дилей за да изчислим какво ще стане с един сигнал, ако този сигнал е пуснат през простия дилей. Това изчисление е показано в следната графика.
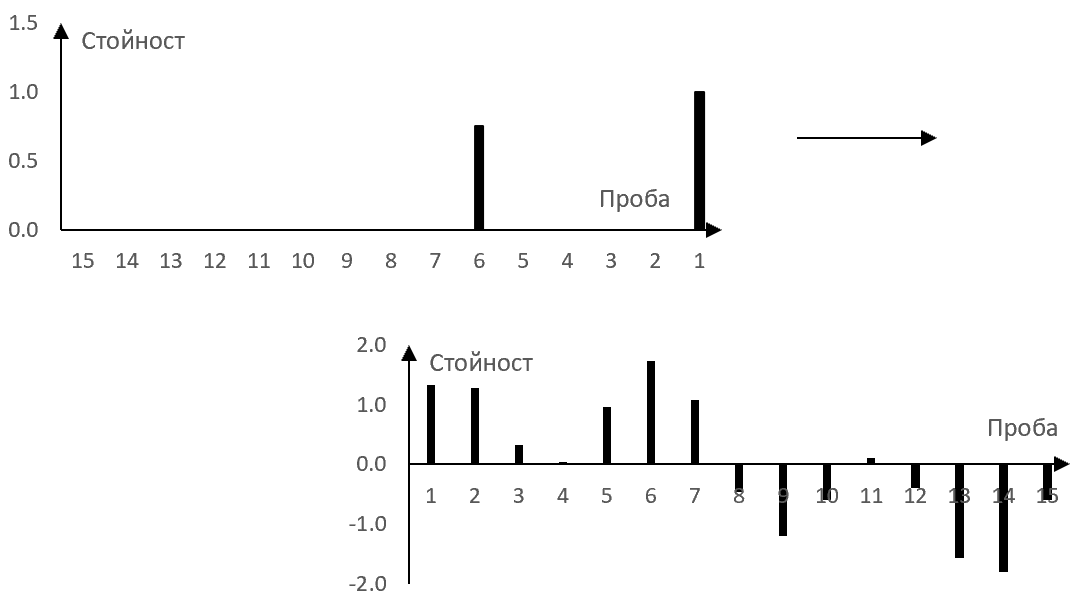
В тази графика, импулсният спектър на примерния прост дилей е отгоре. Стойностите на един примерен сигнал са отдолу.
За да изчислим изходния сигнал на простия дилей, умножаваме пробите на примерния сигнал (отдолу) по пробите на импулсния спектър (отгоре) – обърнат както в графиката – и сумираме резултата. В определената позиция показана в горната графика, стойността на сигнала в проба 7 е умножена по първия, по-голям зъб на импулсния спектър. Стойностите на сигнала при проби 6, 5, 4 и 3 са умножени по нула, тъй като няма съответни зъби в импулсния спектър (той е нула там). Стойността на сигнала при проба 2 е умножена по втория зъб на импулсния спектър и така нататък. Всички получени стойности от тези умножавания се събират.
С други думи, стойността на изходния сигнал при тази проба е равен на стойността на входния сигнал при проба 7 плюс стойността на изходния сигнал при проба 2 с амплитуда 0.75. Това изчисление е изчислението, което очакваме от един прост дилей със забавяне от 5 проби и затихване определено от 75% от амплитудата.
За да изчислим стойността на изходния сигнал при следващата проба, преместваме импулсния спектър с една проба надясно. Стойността на изходния сигнал при следващата проба ще е равен на стойността на входния сигнал при проба 8 с амплитуда 1 плюс стойността на входния сигнал при проба 3 с амплитуда 0.75.
Този процес продължава докато се мине през целия входен сигнал и всички проби на новия сигнал са изчислени. Самият процес – сумирането на умножения (едно средно аритметично, което се мести) – се нарича "конволюция". Ако x(k) е един входен сигнал към простия дилей и a(k) е импулсния спектър на простия дилей с дължина N проби, тогава изходният сигнал y(k) е конволюцията на x(k) и a(k).
$$y(k)=x(k)*a(k)=\sum_{n=0}^{N}a(n)\,x(k-n)$$
Съшият процес се използва и при по-сложни импулсни спектри, като тези по-долу.
Пример: импулсен спектър на един говорител
Следната графика показва първите 10 милисекунди от импулсния спектър на един действителна комбинация от усилвател и говорител за бас. Хоризонталната ос показва времето в секунди и вертикалната ос, както по-горе, показва стойностите на импулсния спектър.
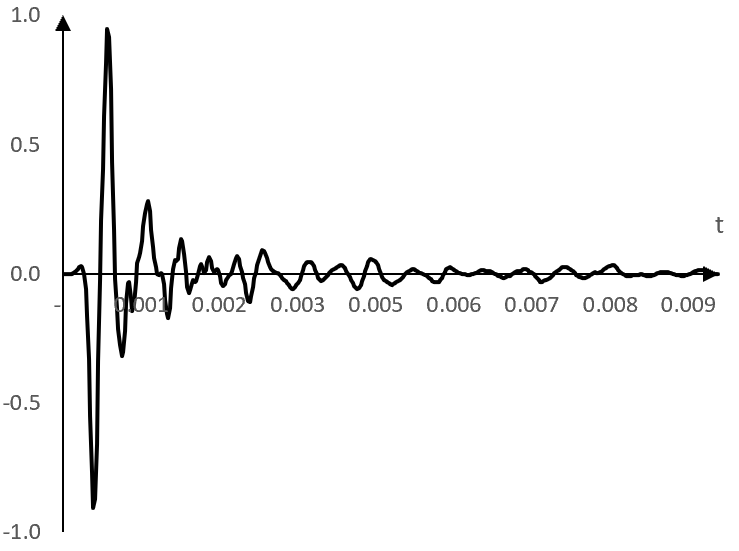
Въпреки че този импулсен спектър е по-сложен от импулсния спектър на простия дилей по-горе, може да се използва по същия начин. Конволюцията на този импулсен спектър с един сигнал ще имитира ефекта, който усилвателят и говорителят за вас ще имат върху сигнала. Виж Orinj Конволюция за да чуеш едно звуково парче преди и след конволюцията с един такъв импулсен спектър.
Ограничен импулсен спектър (FIR)
Следното е формулата за импулсния спектър на един цифров нискочестотен филтър. Един нискочестотен филтър се използва за да пропусне ниските честоти и спре високите честоти, съответно под и над някаква честота, наречена "преходната" честота.
$$a(k)=\begin{cases} \frac{\sin(2\pi \frac{f}{f_s} (k-\frac{N-1}{2}))}{\pi (k-\frac{N-1}{2})}, \, k \ne \frac{N-1}{2} \\ 2 \frac{f}{f_s}, \, k = \frac{N-1}{2} \end{cases}$$
Тук, k са пробите, N е дължината на импулсния спектър в брой проби, fs е пробната честота и f е преходната честота (честотата, около която нискочестотният филтър преминава от един филтър, който пропуска ниските честоти, към един филтър, който спира високите честоти).
Тъй като импулсният спектър може да се приложи към един сигнал със същия процес по-горе – конволюция – стойностите на импулсния спектър a(k) са като тежести в едно средно аритметично. a(k) не е само импулсният спектър, но се нарича и "коефициентите на филтъра" или пък самия "филтър".
Следното е графиката на този филтър с дължина N = 101 проби, пробна честота fs = 2000 Hz и нискочестотна преходна честота f = 40 Hz.
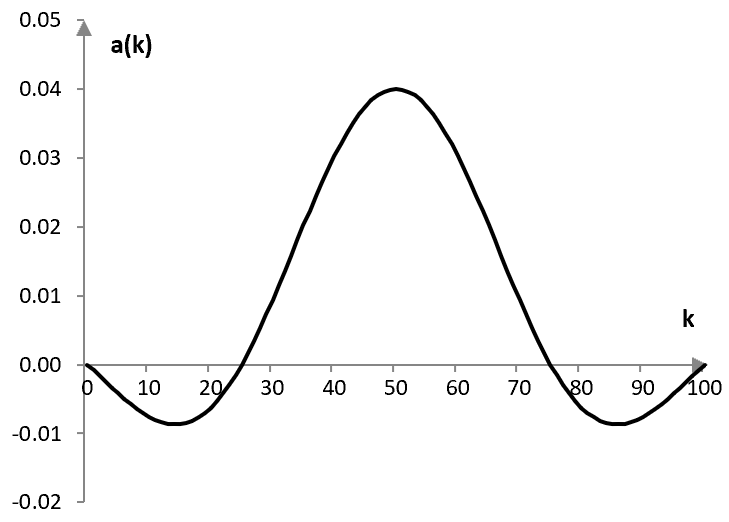
Филтърът не е определен извън своите N точки, но може да бъде определен като равен на 0. На практика, когато използваме такива филтри, това понякога е необходимо. При една конволюция, приравняването на филтъра към 0 извън N-те точки не променя резултата от конволюцията.
Фактът, че импулсният спектър е нула след един ограничен или краен брой точки (N в този пример), прави този филтър един филтър с "ограничен импулсен спектър или "FIR" (от англ., "finite impulse response").
Неограничен импулсен спектър (IIR)
Вземи следния пример на един нискочстотен филтър на Батъруърт.
$$y(k)=0.245\,x(k-1)+1.1581\,y(k-1)-0.4113\,y(k-2)$$
С други думи, изходната стойност y(k) при проба k е равна на сумата (с някакви коефициенти) на входната стойност при предишната проба x(k – 1), изходната стойност при предишната проба y(k – 1) и изходната стойност преди две проби y(k – 2).
Този филтър използва "рекурсия", което означава, че стойностите зависят не само от входния сигнал към филтъра x(k), но и от предишните стойности на изходния сигнал y(k). Ако изпратим един импулс към този филтър, ще получим следния импулсен спектър.
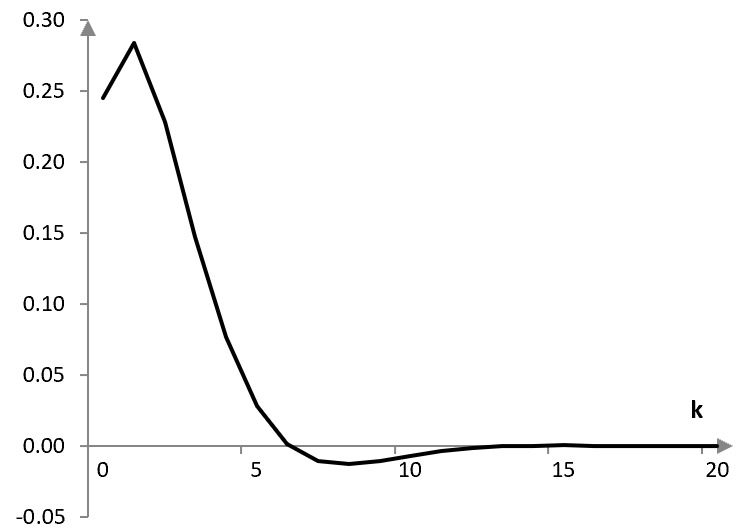
Възможно е този импулсен спектър да е безкрайно дълъг и никога да не стане постоянно равен на нула. Този филтър е един филтър с "неограничен импулсен спектър" или "IIR" (от англ., "infinite impulse response"). На практика, цифровите сигнали могат да имат само един краен брой стойности за амплитудата и този филтър би трябвало да стане нула в един момент, ако изобщо клони към нещо. Така или иначе, нарича се филтър с неограничен импулсен спектър.
Импулсният спектър като едно описание на системата
Когато един импулсен спектър се определя от една функция, както в предишните два примера, функцията се нарича "функция на импулсния спектър ".
Във всички примери тук, импулсният спектър (или пък функцията за импулсния спектър) напълно определя какво прави една система със сигнала. С други думи, импулсният спектър може да се използва за да се определят други свойства на системата, като например нейния амплитуден спектър и фазов спектър.
Следното е амплитудния спектър на примерния импулсен спектър на усилвателя за бас. Изчислен е с преобразуването на Фурие на самия импулсен спектър.
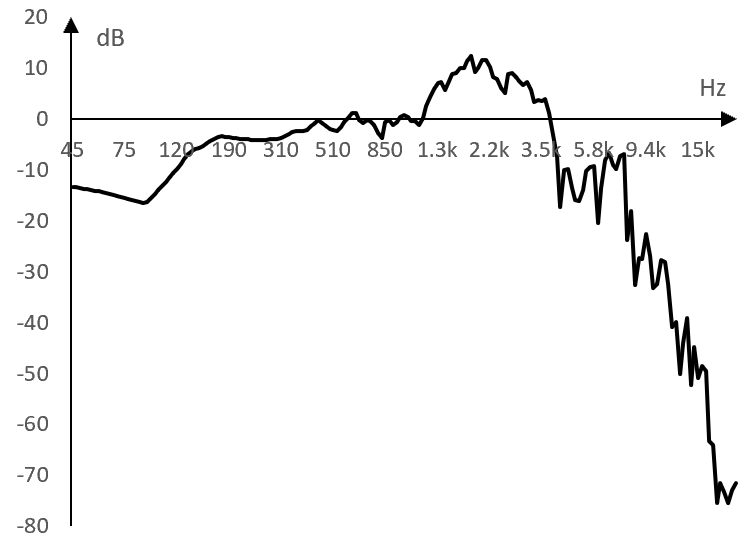
Тази графика ни казва например, че импулсният спектър на този усилвател за бас значително намалява амплитудите на честотите над 9-10 kHz.
Създаване на импулсни спектри
Доста от импулсните спектри тук разчитат на математиката при теорията за работата с цифрови сигнали.
Импулсният спектър на филтъра с ограничен импулсен спектър например разчита на факта, че синусите и косинусите са ортогонални при правилно избрани честоти и интервали (виж анализ на Фурие). Опростено, това означава, че сумите от умноженията, които се използват при конволюцията са приблизително нула за две синусоиди с различни честоти, но не са нула при две синусоиди с една и съща честота. Конволюцията с импулсния спектър ще даде приблизително нула за честоти, които са в сигнала, но не са в самия импулсен спектър. Същата конволюция ще запази честотите, които са и в сигнала, и в импулсния спектър. Тогава, един от начините да се създаде един филтър е просто да се съберат честотите, които импулсният спектър трябва да запази (и да се избягнат честотите, които трябва да се нулират). Горната формула е доста подобна на формулата, която ще получим с този метод (виж Нискочестотен филтър).
Примерният импулсен спектър на усилвателя за баса бе изчислен, като се сравни един входен сигнал към усилвателя със съответния изходен сигнал от усилвателя. Ако изходният сигнал е конволюцията на входния сигнал с импулсния спектър на усилвателя, тогава импулсният спектър е "деконволюпията" на изходния сигнал и входния сигнал. Един пример на това е показан в темата Синусоидно помитане.
Същият метод, който се използва за да се изчисли импулсният спектър на усилвателя за баса, може да се използва и за да се изчислят импулсните спектри на други оборудвания.
Забележи, при усилвателя за баса, че тъй като входният сигнал трябва да се изсвири през усилвателя и изходният сигнал трябва да се запише, импулсният спектър показан по-горе не е само импулсният спектър на усилвателя. Той е импулсният спектър на цялата система, която включва усилвателя, микрофона, оборудването за запис и така нататък.
Добави нов коментар