Преобразуване на Лаплас

Преобразуването на Лаплас се определя от

$$\mathcal{L}(f(t))=\int_0^{\infty} f(t)\,e^{-st}\,dt$$

където s = σ + j ω за ъгловата честота ω и скаларната величина σ. Обратното преобразуване на Лаплас се дава от

$$f(t)=\frac{1}{2\pi i}\lim_{t \rightarrow \infty} \int_{\gamma - iT}^{\gamma+iT}e^{st} \mathcal{L}(f(t)) ds$$

където γ е реално число, което е необходимо за конвергенцията на L(f(t)).

Връзка между преобразуването на Лаплас, преобразуването Z и преобразуването на Фурие

Въпреки че преобразуването на Лаплас е преобразуване на непрекъснати функции, а преобразуването Z е преобразуване на функции в дисретизирано време, изчисленията на тези две преобразувания си приличат. Вместо обаче да произвежда функция на променливата

$$z=A\,e^{-j \omega}$$

преобразуването на Лаплас произвежда функция на променливата

$$s=\sigma+j \, \omega$$

В математиката, когато един непрекъснат сигнал се дискретизира, се използва конволюция на този сигнал с една безкрайна поредица от импулси, наречени гребен на Дирак (безкрайна поредица от делта функции на Дирак (импулси), интегралът на която е едно между отрицателната и положителната безкрайност). Така, ако дискретизираният сигнал x(k), с време на дискретизирането T = 1 / f_s, където f_s е пробната честота, има непрекъснатото представяне x(t), тогава неговото преобразуване на Лаплас е

$$\int_0^\infty x(t) e^{-st}dt=\int_0^\infty (\sum_{k=0}^\infty x(k)\delta(t-kT)e^{-st}) dt$$ $$\sum_{k=0}^\infty (x(k) \int_0^\infty \delta(t-kT)e^{-st}dt)=\sum_{k=0}^\infty x(k) e^{-ksT}$$

Така, преобразуването на Лаплас на един дискретизиран сигнал е едностранното преобразуване Z със z = e^sT. Това означава, че преобразуването на Лаплас е подобно и на преобразуването на Фурие в дискретизирано време, което е специален случай на преобразуването Z (преобразуването Z с A = 1). Преобразуването на Лаплас е подобно и на непрекъснатото преобразуване на Фурие, което е просто преобразуването на Лаплас със σ = 0.

Обосновка за използването на преобразуването на Лаплас при работата с цифрови сигнали

Подобно на преобразуването на Фурие и на преобразуването Z, при работата с цифрови сигнали, можем да кажем, че преобразуването на Лаплас превежда една функция на времето при дадени стойности на амплитудите, честотите и фазите във функция на честотите и фазите при дадени амплитуди и време. Подобно на това, че при работата с цифрови сигнали обикновено използваме преобразуването Z върху кръга с радиус единица (при A = 1 и z = e^{-j ω}), обикновено използваме преобразуването на Лаплас със σ = 0 и s = j ω. Предимството на преобразуването на Лаплас в сравнение на преобразуването Z при работата с цифрови сигнали е просто. Трансферните функции, произведени с преобразуването на Лаплас и изписани като функции на s = j ω са доста по-прости функции на ъгловата честота ω в сравнение с трансферните функции произведени с преобразуването на Фурие и преобразуването Z.

Лесно е, например, да вземем желания амплитуден спектър на нискочестотния филтър на Батъруърт

$$|H(j\omega)|=\frac{G}{\sqrt{1+(\frac{\omega}{\omega_c})^{2n}}}=\frac{G}{\sqrt{1+(\frac{\omega^2}{\omega_c^2})^{n}}}$$

и да видим, че квадрата на трансферната функция, със s = j ω, трябва да е нещо като

$$H(s)^2=\frac{G^2}{1+(\frac{-s^2}{\omega_c^2})^{n}}=\frac{G^2}{1+(\frac{-s}{\omega_c})^{2n}}$$

(Обикновено, вместо H(s)², ще пишем H(s)H(-s). Този вид преобразувания дават излишна информация, когато са приложени върху реални данни и, тъй като искаме да произведем един филтър с реални коефициенти, можем да приемем, че амплитудният спектър е симетричен спрямо нулата и че H(s) = H(-s).) Тогава можем да намерим корените на знаменателя

$$1+(\frac{-s}{\omega_c})^{2n}=0$$ $$s_k=\pm \omega_c e^{\frac{j(2k-1)\pi}{2n}}, k=1,2,...,2n$$

и да изведем

$$H(s)^2=G^2 \prod_{k=1}^{2n} \frac{1}{s-s_k}$$

Знаем, че една стабилна система е тази, която дава нормални (ограничени) изходи за всеки нормален (ограничен) вход. Преобразуването на Лаплас на тези системи трябва да е ограничено. Тъй като на практика работим само с неотрицателни амплитуди, искаме трансферната функция с преобразуването на Лаплас да бъде ограничено за всички s, за които σ = Re(s) ≥ 0. Ако трансферната функция има знаменател с корени, при които тя не е ограничена, тези корени трябва да са с отрицателна реална част.

Сега можем да определим трансферната функция на нискочестотния филтър на Батъруърт по-точно.

$$H(s)=\frac{G\,\omega_c^n}{\prod_{k=1}^n (s-s_k)}, s_k=\omega_c \, e^{\frac{j(2k+n-1)\pi}{2n}}$$

Извеждането на нискочестотния филтър на Батъруърт би било доста по-трудно с преобразуването Z.

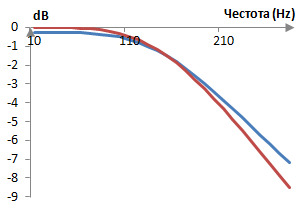
Един от недостатъците на преобразуването на Лаплас е, че това описание на системата за работа с цифрови сигнали в непрекъснато време трябва да се превърне в едно описание на системата в дискретизирано време – обикновено с преобразуването Z. Един от начините да се направи това е да се използва обратното преобразуване на Лаплас. Един друг начин е да се използва билинейното преобразуване. И двата начина са показани в темата Филтър на Батъруърт. Билинейното преобразуване се справя по-добре и е по-лесно за извеждане. Билинейното преобразуване обаче изкривява честотния диапазон. Един цифров филтър на Батъуърт с преходна честота ω_a преди билинейното преобразуване ще има преходната честота ω_d = 2 arctan(ω_a / 2) след билинейното преобразуване. Когато проектираме филтри, трябва да внимаваме да изберем правилната преходна честота. Така или иначе, билинейното преобразуване е подходящо за превръщането на преобразуването на Лаплас в преобразуването Z. Следната графика показва един примерен импулсно инвариантен (с обратното преобразуване на Лаплас) филтър на Батъруърт от втори разряд (в синьо) и същия филтър изчислен с билинейното преобразуване (в червено).

Един втори недостатък е, че преобразуването на Лаплас използва обозначаване, което е по-трудно от обозначаването в преобразуването Z. Свойството за изместването във времето при преобразуването Z например е

$$\mathcal{Z}(x(k-m))=\mathcal{Z}(x(k))z^{-m}$$

Същото свойство за изместването във времето при преобразуването на Лаплас е

$$\mathcal{L}(f(t-a)u(t-a))=\mathcal{L}(f(t))e^{-as}, u=\int_{-\infty}^x \delta(t)dt$$

където u(t) стъпаловидна функция и δ е делта функцията на Дирак.

Трансферни функции с преобразуването на Лаплас

Трансферната функция с преобразуването на Лаплас в една система в непрекъснато време с входен сигнал x(t) и изходен сигнал y(t) е

$$H(s)=\frac{\mathcal{L}(y(t))}{\mathcal{L}(x(t))}$$

Както при преобразуването Z, можем да използваме преобразуването на Лаплас за да изчислим амплитудния и фазовия спектър на системата, но трябва да направим това върху кръга с радиус единица, т.е. при σ = 0 и s = j ω. Амплитудният спектър на една система с трансферната функция по-горе ще е |H(j ω)| а фазовият и спектър е arg(H(j ω)).

Примерни трансферни функции с преобразуването на Лаплас са показани в темите: Филтър бразда, Филтър връх, Филтър на Батъруърт, Филтър на Бесел , Филтър на Чебишев първи вид, Филтър на Чебишев втори вид и Филтър шелф.