admin: First posted on 2013 08 31
This should be an article about deconvolving an actual recorded reverberated sound to produce the impulse of a reverb, but we do not have all the needed tools to do so yet. To get there, we will prepare several articles. Once we are ready – and if we succeed – we should have a reasonably good imitation of the actual reverb and should be able to use the resulting impulse to simulate the actual reverb on any recorded sound.
In any space, we can record a short sound – clap, drum hit, gunshot – together with the actual reverberations of the space. If we can identify the original sound by, say, recording it separately with a microphone that picks up little or none of the reverberation, then we should be able to determine the number and distribution of signal repetitions in the reverberated part. Then, we will have a model of the actual reverb. If the reverb is nice, we will have a way to simulate the nice reverb on other recordings.
To test this theory, we will first create the impulse of an example reverb. This reverb does not have to be great or even realistic. It should be something we can use to, first, create a reverberated sound, and, second, use the reverberated sound to try to recreate the impulse. We will use two things. A tapped delay line will model the early reverb reflections – a small number of repetitions that are somewhat far apart. A Shroeder reverb will model the late part of the reverb – a large number of repetitions that are close together, perhaps with some peaks in the series of repetitions.
The tapped delay line is usually written as
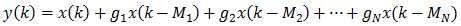
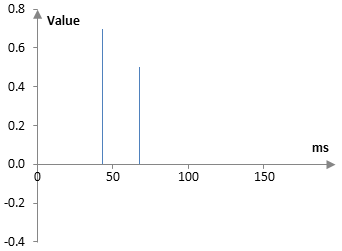
where M1, M2, …, MN are amounts of delay (in samples) and g1, g2, …, gN are gains. To simplify things, we will limit the number of repetitions to two. We will also drop x(k) from the equation to remove the original signal and look at the reverb part only. The original signal can be added later. The following figure shows the impulse response of a tapped delay line with two taps, one with a gain of 0.7 and a delay of 43 ms and one with a gain of 0.5 and a delay of 67 ms. In this whole exercise, we will use a sampling rate of 2000 Hz, which means that the first tap has a delay of 86 samples and the second tap has a delay of 134 samples.
This model of the early reflections is simple enough. The Shroeder reverb model of the late reverb consists of a series of sequential Shroeder all pass filters followed by a set of parallel feedforward comb filers. The all pass filters have the form
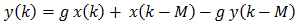
where M is the amount of delay in samples and g is the gain. They create many decaying repetitions of the signal. The comb filters are simply
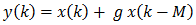
where, again, M is the amount of delay in samples and g is the gain. These comb filters create peaks in the repetitions of the late reverb. We will see these below. We will make a simple late reverb – one with only two all pass filters and only one comb filter.
First, we have to figure out what exactly we should put through the Shroeder reverb – the original signal or the output of the tapped delay line. We can do either, but running the original signal creates an output that is easier to understand and fine tune. The parameters chosen for the tapped delay line above or the all pass and comb filters below are not random. We will use what we see to fine tune them, but more on that later.
The following figure shows the output of the first all pass filter. This filter has M = 3.7 ms and g = 0.7. Since the sampling rate is 2000 Hz, 3.7 ms result in a delay of 7 samples. We will keep the scale of the vertical axes of all figures the same, to make things easier to understand. Since we are putting the original signal through the all pass filters, we will have to both delay and decay the original signal first. Mostly for the sake of having a good looking picture and partly assuming that the repetitions become closer as the reverb progresses, we will delay the original signal by 83 ms. Thus, the difference between the original signal and the first tap of the tapped delay line is about 40 ms, the difference between the first and the second tap of the tapped delay line is about 25 ms, and the difference between the second tap and the all pass filter is about 15 ms. Since the two all pass filter already comes with decays (both of about 0.7), we will use something that will give us somewhat of an exponential decay from the original signal to the first tap, to the second tap, and to the all pass filter – 0.7.
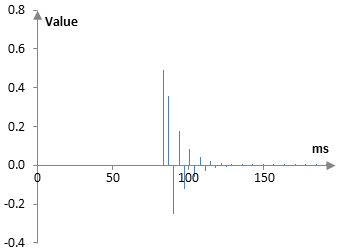
We take this output and run it through the second all pass filter. The second all pass filter has g = 0.65 and M = 1.23 ms (3 samples). It produces a number of additional repetitions. The combination of the two all pass filters is shown in the next figure.
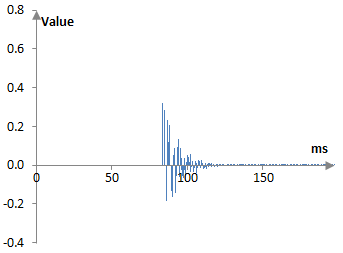
The output of the second all pass filter is used as the input to the feedforward comb filter. It has g = 0.7 and a delay of M = 11 ms (23 samples). The single comb filter produces a single peak of in the repetitions. The output of this filter is also the late reverb – the output of the Shroeder reverb.
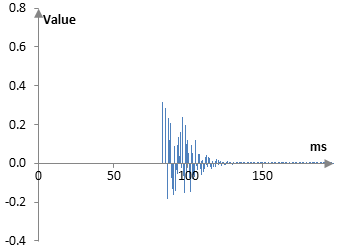
Finally, the total reverb impulse response would simply be the sum of the output of the tapped delay line and the Shroeder reverb (original signal still omitted; we can add it at any time).
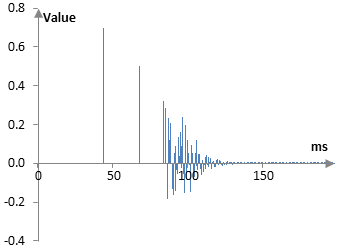
This is the impulse response of the total reverb. In the next article, we will run a fake drum hit through the same set of filters as well as through a convolution with this impulse response to check if the reverberated drum hit matches.
authors: mic
Add new comment