The Chebychev filter of type I is given by the normalized transfer function
$$H(S)=\frac{1}{2^{n-1}\epsilon}\prod_{k=1}^{n}\frac{1}{S-s_k}$$
where n is the order of the filter, ε defines the size of the ripples of the filter's magnitude response in the pass band, and the roots of the denominator sk are
$$s_k=-\sinh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{n})\,\sin(\frac{\pi(2k-1)}{2n})$$ $$-j\,\cosh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{n})\,\cos(\frac{\pi(2k-1)}{2n})$$
Here sinh and cosh are the hyperbolic sine and cosine functions and asinh and acosh are the inverse hyperbolic sine and cosine functions.
The transfer function above is shown irrespective of the cutoff frequency (i.e., for the cutoff frequency 1) and the various forms of the Chebychev type I filter require substitutions. This transfer function is normalized. Use S = s / ωc to get the Chebychev type I low pass filter, where s = jω, ωc is the cutoff frequency of the filter, and ω is the angular frequency spanning the frequency spectrum between 0 and π. Use S = ωc / s to get the Chebychev type I high pass filter. Use S = (s2 + ωc2) / (B s) to get the Chebychev type I band pass filter, where ωc is the midpoint of the pass band and B is the width of the band. Use S = B s / (s2 + ωc2) to get the Chebychev type I band stop filter.
Example: Second order low pass Chebychev type I filter
Set n = 2 and use the substitution S = s / ωc. The transfer function of the second order low pass Chebychev type I filter is
$$H(s)=\frac{1}{2\epsilon}\frac{\omega_c^2}{(s-s_1 \omega_c)(s-s_2 \omega_c)}$$ $$s_1=-\sinh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{2}) \sin(\frac{\pi}{4})+j \, \cosh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{2}) \cos(\frac{\pi}{4})$$ $$s_2=-\sinh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{2}) \sin(\frac{3 \pi}{4})+j \, \cosh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{2}) \cos(\frac{3 \pi}{4})$$ $$=-\sinh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{2}) \sin(\frac{\pi}{4})-j \, \cosh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{2}) \cos(\frac{\pi}{4})$$
Use the bilinear transformation s = 2 (z – 1) / (z + 1) to rewrite the transfer function with the Z transform as follows.
$$H(s)=\frac{\omega_c^2}{2\epsilon}\frac{a_0+a_1 z^{-1}+a_2 z^{-2}}{b_0+b_1 z^{-1}+b_2 z^{-2}}$$ $$a_0=1$$ $$a_1=2$$ $$a_2=1$$ $$b_0=4-2\omega_c(s_1+s_2)+\omega_c^2 s_1 s_2$$ $$b_1=-8+2\omega_c^2 s_1 s_2$$ $$b_2=4+2\omega_c(s_1+s_2)+\omega_c^2 s_1 s_2$$
(All coefficients in the transfer function are real as s1 and s2 are complex conjugates). Say that the cutoff frequency of the filter is ωc = 0.6 and that ε = 0.5 (technically, the cutoff frequency of the filter will be ωc = 2 arctan(0.6/2) ≈ 0.583, due to the warping of the frequency domain by the bilinear transformation). The transfer function of this example Chebychev type I low pass filter, after scaling to obtain b0 = 1 is
$$H(z)=\frac{0.062755-0.125509z^{-1}+0.062755z^{-2}}{1-1.254222z^{-1}+0.534869z^{-2}}$$
and the filter itself is
$$y(k) = 0.062755 x(k) – 0.125509 x(k – 1) + 0.062755 x(k – 2)$$ $$+ 1.254222 y(k – 1) – 0.534869 y(k – 2)$$
Suppose that the sampling frequency is 2000 Hz. The cutoff frequency then is ωc = (0.6 * 2000) / (2 ω) = 191 Hz. The magnitude response of the filter is shown in the graph below.
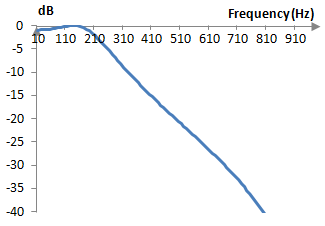
Size of the ripples in the pass band
The magnitude function of the Chebychev type I low pass filter can also be written as follows.
$$|H(j\omega)|=\frac{1}{\sqrt{1+\epsilon^2 T_n^2(\frac{\omega}{\omega_c})}}$$
where Tn are the Chebychev polynomials
$$T_n(x)=\begin{cases} \cos(n\,\mathrm{acos}(x)) & |x|\le1 \\ \cosh(n \, \mathrm{acosh}(x)) & |x|\gt 1\end{cases}$$
In the pass band, where ω / ωc < 1, Tn (ω / ωc) = \cos(n \mathrm{acos}(ω / ωc)) and 0 ≤ Tn2(ω / ωc) ≤ 1. In the pass band
$$\frac{1}{\sqrt{1+\epsilon^2}}\le|H(j\omega)|\le1$$
Thus, smaller ε implies smaller ripples in the pass band and larger ε implies larger ripples. It should also be expected that |H(jω)| = 1 at ω / ωc = \cos(π / 2n), since then Tn(ω / ωc) = 0.
Using the same parameters as above, namely n = 2 and ωc = 0.6, we can plot the |H(jω)| for three different values of ε (0.25, 0.5, and 0.75).
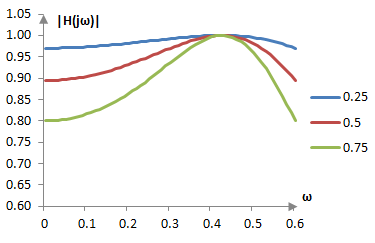
The magnitude response of the three corresponding filters for a portion of the frequency spectrum (up to 600 Hz) is:
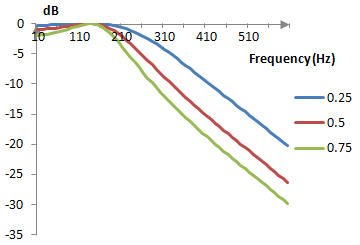
A larger ε creates a filter with a better stop band attenuation, but with larger ripples in the pass band. A smaller ε creates a filter with smaller ripples in the pass band, but with worse stop band attenuation.
Example: Second order high pass Chebychev type I filter
Set n = 2 and S = ωc / s. The transfer function of the second order high pass Chebychev type I filter is
$$H(s)=\frac{1}{2\epsilon}\frac{s^2}{(\omega_c-s_1 s)(\omega_c-s_2 s)}$$
s1 and s2 are as before. After the bilinear transformation s = 2 (z – 1) / (z + 1), the transfer function becomes
$$H(z)=\frac{1}{2\epsilon}\frac{a_0+a_1z^{-1}+a_2z^{-2}}{b_0+b_1z^{-1}+b_2z^{-2}}$$ $$a_0=4$$ $$a_1=-8$$ $$a_2=4$$ $$b_0=\omega_c^2-2\omega_c(s_1+s_2)+4s_1s_2$$ $$b_1=2\omega_c^2-8s_1s_2$$ $$b_2=\omega_c^2+2\omega_c(s_1+s_2)+4s_1s_2$$
If, for example, we use the cutoff frequency ωc = 0.6 and ε = 0.5, and we scale the coefficients to obtain b0 = 1, then a0 = a2 = 0.648689, a1 = -1.297379, b0 = 1, b1 = -1.333750, b2 = 0.567278. If we suppose that the sampling frequency is 2000 Hz, then ωc = (0.6 * 2000) / (2 π) = 191 Hz and the magnitude response of the filter is as follows.
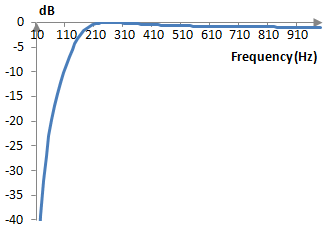
Higher order Chebychev type I filters
Higher order Chebychev type I filters can be designed either using the methods above, or by stacking lower order filters. For example, the transfer function for the fourth order high pass Chebychev type I filter can be written as
$$H(s)=\frac{1}{8\epsilon} \frac{s^2}{(\omega_c-s_1s)(\omega_c-s_4s)} \frac{s^2}{(\omega_c-s_2s)(\omega_c-s_3s)}$$
This means that the fourth order high pass Chebychev type I filter can be implemented by stacking two filters of order two (these are not Chebychev type I filters, as the roots of each filter of order two differ from the Chebychev roots). Multiplying two transfer functions means that the impulse response of the total filter is the convolution of the two impulse responses of the lower order filters and the output of the first filter is the input to the second filter. We combine the roots in the manner above, as s1 and s4 are complex conjugates and as s2 and s3 are complex conjugates. It is not important whether (1 / 8ε) is used in the first filter, the second filter, or split between the two.
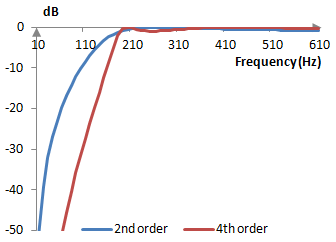
The following is a comparison of the magnitude responses of the fourth order and second order Chebychef type I filters with ε = 0.5, sampling frequency of 2000 Hz, and ωc = 0.6.
Comments
Thanks
Thanks
Add new comment