The bilateral Z transform is
$$Z(x(k))=\sum_{k=-\infty}^{\infty} x(k) \, z^{-k}$$
where z = A e-j ω for some real number A.
Motivation for using the Z transform in digital signal processing
The Z transform is a generalization of the discrete-time Fourier transform, which is defined as
$$H(\omega)=\sum_{k=-\infty}^{\infty} x(k) \, e^{-j \, \omega \, k}$$
As with other Fourier transforms, the discrete-time Fourier transform translates a complex valued signal x(k) as a function of time into a set of complex numbers that carry the frequency and phase of each simple wave in the signal. The discrete-time Fourier transform is used when x(k) is discrete, but not of finite duration and not periodic (alternatively, one can use the continuous or the discrete Fourier transform). The discrete-time Fourier transform is often thought of as the logical result of sampling the input to the continuous Fourier transform x(t) into discrete time x(n).
The bilateral Z transform generalizes the discrete-time Fourier transform by introducing the real number A, which represents the magnitude of the transform basis A e-j ω k.
$$H(\omega)=\sum_{k=-\infty}^{\infty} x(k) \, z^{-k}=\sum_{k=-\infty}^{\infty} x(k) \, A \, e^{-j \, \omega \, k}$$
Alternatively, the discrete-time Fourier transform is simply the Z transform with A = 1. When A = 1, the transform basis becomes the numbers e-j ω k, which in the complex plane form a circle of radius 1 around the origin. Thus, we can say that the discrete-time Fourier transform is the Z transform evaluated on the unit circle.
The motivation behind using the discrete-time Fourier transform in digital signal processing is that it allows us to use a discrete signal, but a continuous set of frequencies and phases. The motivation behind using the Z transform in digital signal processing rather than the discrete-time Fourier transform is only that it significantly reduces notation. In fact, in digital signal processing we will always evaluate the Z transform on the unit circle – with A = 1 – which means that we will only really use the discrete-time Fourier transform and we will never use its generalized form – the Z transform. We do however use the Z transform notation. It is much easier to write z-k rather than e-j ω k.
Some useful properties of the Z transform
One useful property of the Z transform is that it is linear, much like the Fourier transforms.
$$Z(a_1 x_1(k) + a_2 x_2(k))=a_1 Z(x_1(k))+a_2 Z(x_2(k))$$
Second, time-shifting of the signal x(k) results in the following.
$$Z(x(k-m))=\sum_{k=-\infty}^{\infty} x(k-m) \, z^{-k}$$ $$=\sum_{k=-\infty}^{\infty} x(k-m) z^{-(k-m)} z^{-m}=Z(x(k)) \, z^{-m}$$
This means that, if the output of a system a(k) on the input x(k) is given by
$$y(k)=\sum_{n=0}^{N-1} a(n) \, x(k-n)$$
where a(k) is a finite impulse response filter, then
$$Z(y(k))=Z(\sum_{n=0}^{N-1} a(n) \, x(k-n))=(\sum_{n=0}^{N-1} a(n) \, z^{-n}) Z(x(k))$$
and
$$H(z)=\frac{Z(y(k))}{Z(x(k))}=\sum_{n=0}^{N-1} a(n) \, z^{-n}$$
which is the transfer function of the system a(k). This transfer function has nice properties. In linear time-invariant systems, the magnitude |H(z)| of H(z), z = A e-j ω, when evaluated at A = 1 (on the unit circle), produces the magnitude response of the system
$$|H(e^{-j \, \omega})|=\sqrt{Re(H(e^{-j \, \omega}))^2+Im(H(e^{-j \, \omega}))^2}$$
The phase response of the system is
$$\Phi(e^{-j \, \omega})=\mathrm{atan2}(\frac{Im(H(e^{-j \, \omega}))}{Re(H(e^{-j \, \omega}))})$$
The notation |H(e-j ω)| and Φ(e-j ω) is used to show that the magnitude response and phase response are evaluated with e-j ω and not with z = A e-j ω.
Example transfer functions of a comb filter with the Z transform
A feedforward comb filter is just a simple delay. It has the form
$$y(k)=x(k)+g \, x(k-m)$$
where g is some gain, 1 – g is the decay of the delayed signal, and m is the delay in number of samples. The Z transform of both sides of the above equation produces
$$Z(y(k))=Z(x(k)+g \, x(k-m))=Z(x(k))+g \, z^{-m} Z(x(k))=Z(x(k))(1+g \, z^{-m})$$
The transfer function of this comb filter then is
$$H(z)=\frac{Z(y(k))}{Z(x(k))}=1+g \, z^{-m}$$
The magnitude response of the comb filter at a particular frequency ω is
$$H(e^{-j \, \omega})=|1+g \, z^{-m}|=|1+g \, e^{-j\, \omega \, m}| = |1+g \, \cos(\omega \, m)-g \, \sin(\omega \, m)| $$ $$= \sqrt{(1+g \, \cos(\omega \, m))^2+(g \, \sin(\omega \, m))^2}= \sqrt{(1+g)^2+2 \, g \, \cos(\omega \, m)}$$
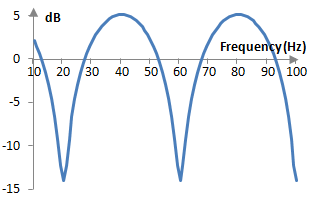
This function of ω, when plotted, produces the characteristic comb like magnitude response of the comb filter shown below. This example feedforward comb filter was computed with the sampling frequency fs = 2000 Hz, a delay of m = 50 samples, and with g = 0.8.
Other examples
For other examples of using the Z transform, see the topics on Comb filter, Transfer function, Gibbs phenomenon, Butterworth filter, All pass filter, and Shroeder-Moorer filter.
Add new comment