The Blackman window coefficients are given by the following formula
$$a(k)=0.42-0.5 \, \cos(\frac{2\pi k}{N-1})+0.08 \, \cos(\frac{4 \pi k}{N-1})$$
where N is the length of the filter and k = 0, 1, …, N – 1.
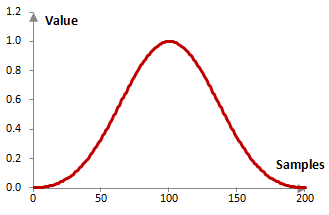
An example Blackman window
Consider a finite impulse response (FIR) low pass filter of length N = 201. The following is the Blackman window.
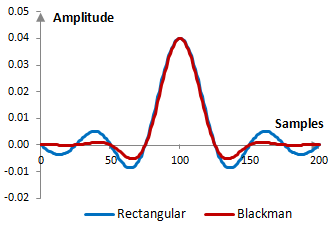
Given a sampling frequency of 2000 Hz and a filter cutoff frequency of 40 Hz, the impulse response of the filter with a rectangular window (with no window) and with the Blackman window is as follows.
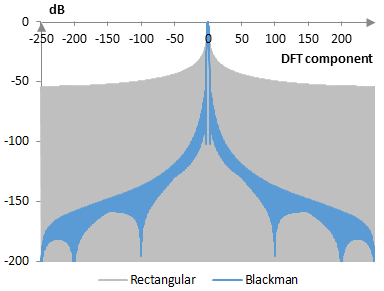
The magnitude response of the same filter is shown on the graph below.

Assuming the Blackman window is of sufficient length, it will usually produce stop band attenuation of approximately -75 dB (although it could be as high as -25 dB for short filters) and ripples in the pass band of approximately +/- 0.003 dB. Given the sampling frequency fs, a filter of length N with the Blackman window transitions from 0 dB to -20 dB in a transition band of approximately fs (4.68 / N) and to the stop band in a transition band of approximately fs (6.46 / N). This means, for example, that an appropriate filter length, given a desired transition band, is N = 6.46 / (transition / fs).
Measures for the Blackman window
The following graph compares the discrete Fourier transform of the Blackman window and the rectangular window.
The Blackman window measures are as follows.
| Coherent gain | 0.42 |
| Equivalent noise bandwidth | 1.73 |
| Processing gain | -2.38 dB |
| Scalloping loss | -1.09 dB |
| Worst case processing loss | -3.48 dB |
| Highest sidelobe level | -58.1 dB |
| Sidelobe falloff | -21.6 dB / octave, -71.7 dB / decade |
| Main lobe is -3 dB | 1.64 bins |
| Main lobe is -6 dB | 2.30 bins |
| Overlap correlation at 50% overlap | 0.089 |
| Amplitude flatness at 50% overlap | 0.680 |
| Overlap correlation at 75% overlap | 0.565 |
| Amplitude flatness at 75% overlap | 1.000 |
Generalized Blackman windows
In principle, the window above is the most commonly used Blackman window. A more general definition of the Blackman window is
$$a(k)=a_0-a_1 \, \cos(\frac{2\pi k}{N-1})+a_2 \, \cos(\frac{4 \pi k}{N-1})$$ $$a_0=\frac{1-\alpha}{2}, a_1=\frac{1}{2}, a_2=\frac{\alpha}{2}$$
The Blackman window above uses α = 0.16, which is a common approximation of the exact Blackman window with a0 = 7938 / 18608, a1 = 9240 / 18608, and a2 = 1430 / 18608.
As α approaches zero or 1, the Blackman window becomes a cosine window (of two different frequencies in the two different cases). The following is the Blackman window for three different values of α: 0.05, 0.16, and 0.4.
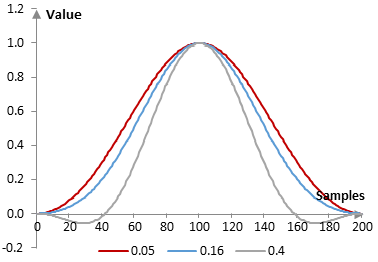
The following are the corresponding impulse responses for the same filter used in the first example above.
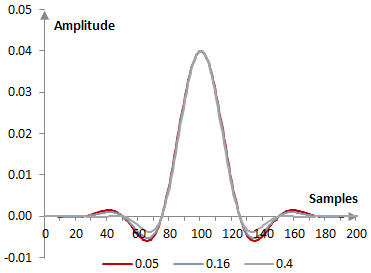
The following are the corresponding magnitude responses.
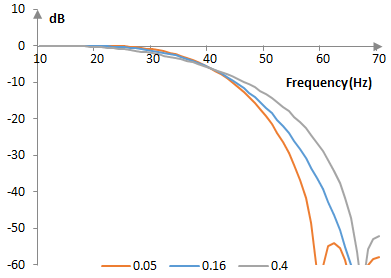
The Blackman window is a generalized cosine window (see Hamming window).
Measures for the generalized Blackman windows
The following are measures for selected generalized Blackman windows.
| Exact Blackman | Generalized α = 0.05 |
Generalized α = 0.20 |
Generalized α = 0.35 |
|
| Coherent gain | 0.43 | 0.47 | 0.40 | 0.32 |
| Equivalent noise bandwidth | 1.70 | 1.56 | 1.82 | 2.33 |
| Processing gain (dB) | -2.30 | -1.93 | -2.59 | -3.68 |
| Scalloping loss (dB) | -1.15 | -1.33 | -1.00 | -0.53 |
| Worst case processing loss (dB) | -3.44 | -3.25 | -3.59 | -4.21 |
| Highest sidelobe level (dB) | -68.7 | -37.3 | -56.5 | -38.1 |
| Sidelobe falloff (dB / octave, dB / decade) | -10.0, -33.3 | -20.9, -69.5 | -22.1, -73.4 | -21.2, -70.5 |
| Main lobe is -3 dB (bins) | 1.60 | 1.50 | 1.72 | 2.28 |
| Main lobe is -6 dB (bins) | 2.26 | 2.08 | 2.42 | 3.08 |
| Overlap correlation at 50% overlap | 0.099 | 0.143 | 0.068 | -0.008 |
| Amplitude flatness at 50% overlap | 0.695 | 0.900 | 0.600 | 0.300 |
| Overlap correlation at 75% overlap | 0.576 | 0.635 | 0.532 | 0.365 |
| Amplitude flatness at 75% overlap | 1.000 | 1.000 | 1.000 | 1.000 |
See also:
Window
Comments
Can you help me translate
i am from Italy hello. Can you help me translate?
No, sorry
Add new comment