Нивото 1 на преобразуването с вълнички Daub4 на Дубеши на сигнала x(k) с дължина N е x → (b1 | a1), където a1 и b1 са вектори с дължина N/2, изчислени от x чрез произведенията
$$a_1=(A_1*x,A_2*x,...,A_{N/2}*x)$$ $$b_1=(B_1*x,B_2*x,...,B_{N/2}*x)$$
с векторите с дължина N
$$A_1=(\frac{1+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{3-\sqrt{3}}{4\sqrt{2}},\frac{1-\sqrt{3}}{4\sqrt{2}},0,0,0,0,...,0,0,0,0,0)$$ $$A_2=(0,0,\frac{1+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{3-\sqrt{3}}{4\sqrt{2}},\frac{1-\sqrt{3}}{4\sqrt{2}},0,0,...,0,0,0,0,0)$$ $$A_3=(0,0,0,0,\frac{1+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{3-\sqrt{3}}{4\sqrt{2}},\frac{1-\sqrt{3}}{4\sqrt{2}},...,0,0,0,0,0)$$ $$...$$ $$A_{\frac{N}{2}-1}=(0,0,0,0,0,0,0,0,...,\frac{1+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{3-\sqrt{3}}{4\sqrt{2}},\frac{1-\sqrt{3}}{4\sqrt{2}})$$ $$A_{\frac{N}{2}}=(\frac{3-\sqrt{3}}{4\sqrt{2}},\frac{1-\sqrt{3}}{4\sqrt{2}},0,0,0,0,0,0,...,0,0,\frac{1+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}})$$
и
$$B_1=(\frac{1-\sqrt{3}}{4\sqrt{2}},\frac{-3+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{-1-\sqrt{3}}{4\sqrt{2}},0,0,0,0,...,0,0,0,0,0)$$ $$B_2=(0,0,\frac{1-\sqrt{3}}{4\sqrt{2}},\frac{-3+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{-1-\sqrt{3}}{4\sqrt{2}},0,0,...,0,0,0,0,0)$$ $$B_3=(0,0,0,0,\frac{1-\sqrt{3}}{4\sqrt{2}},\frac{-3+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{-1-\sqrt{3}}{4\sqrt{2}},...,0,0,0,0,0)$$ $$...$$ $$B_{\frac{N}{2}-1}=(0,0,0,0,0,0,0,0,...,\frac{1-\sqrt{3}}{4\sqrt{2}},\frac{-3+\sqrt{3}}{4\sqrt{2}},\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{-1-\sqrt{3}}{4\sqrt{2}})$$ $$B_{\frac{N}{2}}=(\frac{3+\sqrt{3}}{4\sqrt{2}},\frac{-1-\sqrt{3}}{4\sqrt{2}},0,0,0,0,0,0,...,0,0,\frac{1-\sqrt{3}}{4\sqrt{2}},\frac{-3+\sqrt{3}}{4\sqrt{2}})$$
Нивото 2 на преобразуването с вълнички Daub4 на Дубеши е x → (b1 | b2 | a2), където a2 и b2 са нивото 1 преобразуване с вълнички Daub4 на Дубеши на a1, изчислено с векторите A и B с дължина N / 2. Нивото N на преобразуването с вълнички Daub4 на Дубеши е изчислено, като преобразуванията на частите "a" на предишното ниво на преобразуването се вземат едно след друго, с вектори които са с дължина равна на половината от дължината на предишното преобразуване.
Забележи, че x(k) може да се възстанови от a1 и b1 с изчислението
$$x(k)=\sum_{i=0}^{N-1}A_i(k)a_1(i)+\sum_{i=0}^{N-1}B_i(k)b_1(i)$$
При нивото 2 на преобразуването, a1 може да се възстанови от a2 и b2 и следователно x(k) може да се възстанови от b1, b2 и a2 (следователно, a1 е пропуснато от определението на преобразуването x → (b1 | b2 | a2)).
При всяка следваща стъпка, векторите "a" и "b" са с дължина равна на половината от дължината на векторите при предишното ниво на преобразуването. Така, ако N = 2n за някакво цяло число n, можем да изпишем x → (b1 | b2 | … | bN-1 | aN-1), където aN-1 и bN-1 са вектори с дължина 2 (за разлика от преобразуването с вълнички на Хаар, не можем да стигнем до нивото N и векторите aN и bN с дължина 1, защото векторите A и B имат четири ненулеви стойности, вместо само две). Забележи, че b1 е с дължина N / 2, b2 е с дължина N / 4 и така нататък. Общата дължина на b1, b2, …, bN-1, aN-1 е N и така тези вектори носят същото количество информация, като x(k). Тъй като x(k) може да се възстанови от тези вектори, те носят същата информация, като x(k).
Както при преобразуването с вълнички на Хаар, a1 е средно аритметично на x(k) и е "тенденцията" на сигнала. b1 съдържа колебанията, които a1 премахва. a1 е изчислено чрез конволюцията на сигнала x(k) с A1 (с разликата, че стъпката на тази конволюция е две проби, вместо една). b1 е конволюцията на сигнала x(k) с B1. С други думи, a1 and b1 са резултатите от един нискочестотен филтър и един високочестотен филтър върху x(k) (векторите A1 и B1). По същия начин, a2 и b2 са тенденцията и колебанията на a1 и така нататък.
Преобразуването с вълнички Daub4 е само едно от преобразуванията с вълнички на Дубеши.
Един пример на компресиране на данните с преобразуването с вълнички Daub4 на Дубеши
Вземи сигнала x(k) с дължина N = 256 който съдържа две прости вълни с честоти 5 Hz и 9 Hz, при пробната честота 256 Hz. Фазата на честотата 9 Hz е 10 проби и фазата на честотата 5 Hz е нула. Сигналът е
$$x(k)=\sin(\frac{2\pi\,k\,5}{256})+\sin(\frac{2\pi\,(k-10)\,9}{256})$$
Един подробен пример на компресирането на този сигнал е даден в темата Преобразуване с вълнички на Хаар. Примерът тук сравнява резултатите от преобразуванията с вълнички на Хаар и с вълничките на Daub4 на Дубеши.
Разложи сигнала с преобразуването с вълнички Daub4 на Дубеши в b1, b2, …, b7 и a7. Подреди стойностите на всички тези вектори (в една единствена поредица) и премахни най малките стойности (замени ги с 0). Ако трябва да изпратим този сигнал, можем да изпратим само ненулевите стойности. Можем да използваме само няколко байтове, за да отбележим къде тези ненулеви стойности трябва да се сложат, когато векторите b1, …, a7 се възстановяват и тогава можем да възстановим сигнала x(k) от тези вектори. Тогава ще използваме по-малко данни, отколкото самият сигнал x(k).
В примера в темата Преобразуване с вълнички на Хаар например, ако половината от стойностите се махнат (по-малките стойности), преобразуването запазва 99.5% от енергията на сигнала, където енергията е изчислена като сумата на квадратите на стойностите на преобразуването. Тъй като половината от стойностите бяха нулирани, отношението на компресиране в този пример бе 2:1. При преобразуването с вълнички Daub4 на Дубеши, 99.5% от енергията на сигнала е запазена ако само една пета от стойностите на сигнала са оставени и четири пети са нулирани. Тоест, същата енергия се запазва с отношение на компресиране равно на 5:1. Ако компресиране 5:1 се използва при преобразуването с вълнички на Хаар, загубата на енергия ще е над 5%, което е значително.
Възстановения сигнал x(k), след като няколко стойности са махнати от векторите b1, …, a7, не е същия, като оригиналния, разбира се. Следните графики показва двата сигнала.
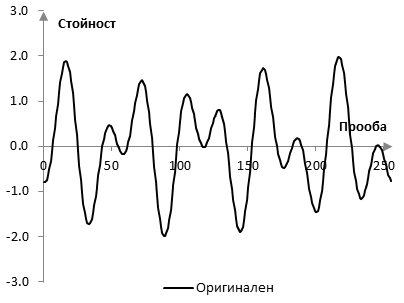
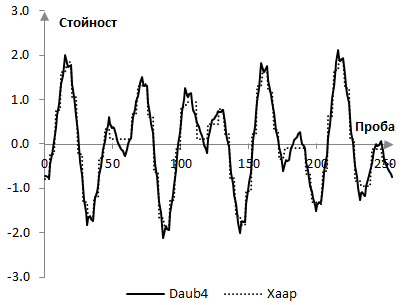
Честотното съдържание на възстановения сигнал също е различно. Следните две графики показват преобразуването на Фурие на оригиналния и възстановения синал.
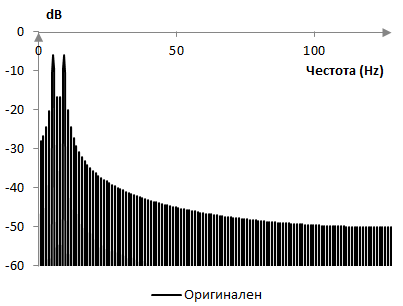
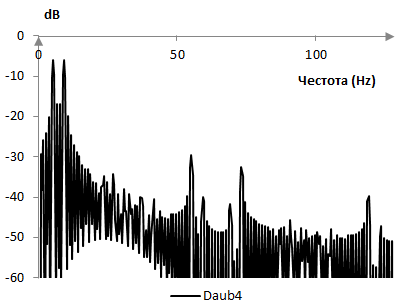
Добави нов коментар