The scalloping loss of a window a(k) of length N is
$$SL=\frac{|\sum_{k=0}^{N-1}a(k) e^{-\frac{j \pi k}{N}}|}{\sum_{k=0}^{N-1}a(k)}=\frac{\sqrt{(\sum_{k=0}^{N-1} a(k) \cos(\frac{\pi k}{N}))^2+(\sum_{k=0}^{N-1} a(k) \sin(\frac{\pi k}{N}))^2}}{\sum_{k=0}^{N-1} a(k)}$$
The scalloping loss is the coherent gain of a frequency half a bin from a component on the discrete Fourier transform divided by the coherent gain of the window, as explained below.
Motivation for the scalloping loss
The following is a graph of the maximum value of the discrete Fourier transform of 40 points taken on simple sine waves with various frequencies between 20 Hz and 80 Hz, where the sampling frequency is 400 Hz.
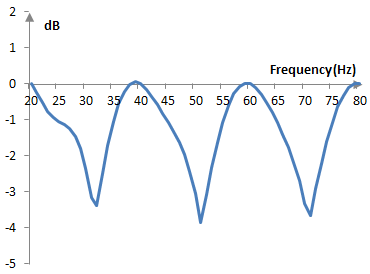
The graph resembles a scallop (the decorative loops in curtains or tablecloths). The largest "loss", the places where the Fourier transform is least precise, occurs (approximately) in the middle between the transform components. At the sampling rate of 400 Hz, a transform of 40 points will have components 0 Hz, 20, Hz, 40, Hz, …, 380 Hz. The largest loss occurs at 30 Hz, 50 Hz, and so on. Thus, the scalloping loss is said to be the largest loss due to the frequency.
Scalloping loss and windows
Consider the following graph.
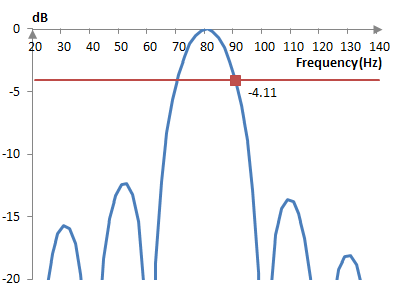
This is the discrete Fourier transform (DFT) of 20 components of the sine wave of 80 Hz, sampled at the sampling frequency 400 Hz. Rather than taking the DFT of the wave simply at the 20 DFT components (0 Hz, 20 Hz, 40 Hz, …, 380 Hz), however, the graph also shows the DFT at frequencies in between the DFT components. If the DFT was taken only at its components, then the graph will show only 0 dB at 80 Hz and practically very large negative numbers at all other components, since the DFT there is approximately zero. In between the components, however, there is spectral leakage. At half a component, at 0.5, we get -4.11 dB. This is the scalloping loss with no window (of the rectangular window).
Suppose that we apply the Hann window of 20 points to the sine wave of 80 Hz before computing the DFT. The result is shown below. The DFT after the Hann window is shown as a solid line. The DFT without the window is shown as a dashed line.
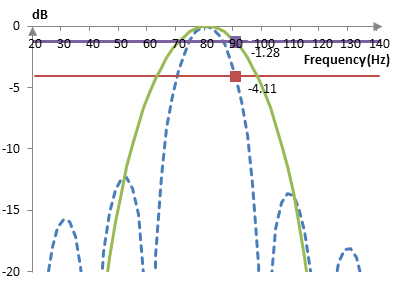
The DFT after the Hann window in this graph is adjusted for the coherent gain of the window. The scalloping loss with the Hann window is -1.28 dB. Thus, the scalloping loss is a measure of the shape of the main lobe of the DFT of the window.
This is, of course, a computation of the scalloping loss at half a component of the DFT after some randomly chosen frequency for a very short window. With the formula above and for larger windows, the scalloping loss of the Hann window would be approximately -1.42 dB (typically noted without the minus sign, as it is a "loss").
Scalloping loss for common windows
The following is the scalloping loss (in dB) of some common windows (with the window definitions on this site).
| Bartlett-Hann | -1.51 |
| Blackman Exact Blackman Generalized Blackman α = 0.05 α = 0.20 α = 0.35 |
-1.09 -1.15 -1.33 |
| Blackman-Harris | -0.82 |
| Blackman-Nuttall | -0.85 |
| Bohman | -1.02 |
| Dolph-Chebychev ω0 = 0.1 ω0 = 0.2 ω0 = 0.3 |
-1.44 -1.28 -1.23 |
| Flat top | -0.01 |
| Gaussian σ = 0.3 σ = 0.5 σ = 0.7 Approximate confined Gaussian σ = 0.3 σ = 0.5 σ = 0.7 Generalized normal α = 2 α = 4 α = 6 |
-0.95 -2.12 -2.84 -0.95 -2.12 |
| Hamming | -1.75 |
| Hann | -1.42 |
| Hann-Poisson α = 0.3 α = 0.5 α = 0.7 |
-1.32 -1.25 -1.19 |
| Kaiser α = 0.5 α = 1.0 α = 5.0 |
-3.31 -2.42 -1.05 |
| Kaiser-Bessel | -1.02 |
| Lanczos | -1.88 |
| Nuttall | -0.81 |
| Parzen | -2.57 |
| Planck-taper ε = 0.2 ε = 0.4 ε = 0.5 |
-2.46 -1.51 -1.20 |
| Poisson α = 0.2 α = 0.5 α = 0.8 |
-3.69 -3.36 -3.05 |
| Power of cosine α = 1.0 α = 2.0 α = 3.0 |
-2.09 -1.42 -1.07 |
| Rectangular | 3.92 |
| Sine | -2.09 |
| Triangular | -1.82 |
| Tukey α = 0.3 α = 0.5 α = 0.7 |
-1.81 -2.23 -2.79 |
| Ultraspherical (x0 = 1) μ = 2 μ = 3 μ = 4 |
-2.32 -1.66 -1.30 |
| Welch | -2.23 |
Comments
In duplicating these values
In duplicating these values in my own tests, there
seems to be a factor of 2 off. To match your values,
I had to write the following line of code.
* return 20.0 * Math.log10((Math.sqrt(sumX * sumX + sumY * sumY) / sumA));
Is there a factor of 2 lurking somewhere in the equations
or are the values off by a factor of 2?
I just checked a couple (the
I just checked a couple (the Bartlett-Hann and the Hann) and the values above are OK. Your formula is also OK. Is this just the difference between the power decibel (10 * log10 ()) and the amplitude decibel (20 * log10())?
Hann window value error?
Value stated for Hann window in paragraph is -1.28 and it says -1.42 in table
It is -1.42
It is -1.42. The -1.28 value was supposed to be a simple illustration, computed with a short Hann window and not with the actual formula above, but with the DFT over a random frequency. Sorry for this confusion and thanks for pointing this out. We tried to explain why the scalloping loss is an interesting measure, but I can see how the middle of the article above doesn't actually explain much. I'll have to revise the text above at some point.
Add new comment