администратор: Качено първо на 2012 01 19
Работехме върху версия 3 на Orinj. Искахме да подобрим графиките на няколко от ефектите DSP в Orinj и да покажем действителния амплитуден спектър на ефекта. Това включваше ефекти, които имат графики с еквилизация или с някакви честотни филтри – графичния и параметричния еквилайзер, ривърба (заради параметричния му еквилайзер) и филтъра бразда. Тази статия е за изчисляването на действителния амплитуден спектър бързо и ефикасно.
Действителен амплитуден спектър на параметричния еквилайзер в Orinj
Следното е амплитудния спектър на параметричния еквилайзер в Orinj с настройката за "яркост и бас".
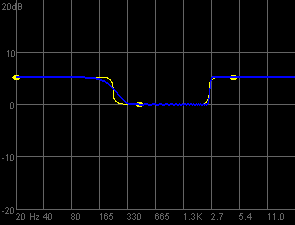
Жълтата линия показва желания амплитуден спектър на еквилайзера, който добавя около 5 dB към амплитудата на честотите под 230 Hz и на честотите над 2500 Hz. Синята линия показва действителния амплитуден спектър на еквилайзера. Има две разлики. Тъй като еквилайзера използва честотни филтри с ограничени импулсни спектри, които имат обикновените вълни на феномена на Гибс, в действителния амплитуден спектър има вълни. Тъй като е трудно да се получи един прехода в амплитудата при ниските честоти, преходната лента при действителния амплитуден спектър между 5-те dB и 0-та при ниските честоти не е толкова кратка, както преходната лента при желания амплитуден спектър. Тази нова графика е много по-добра, от графиката в параметричния еквилайзер в предната версия 2 на Orinj, тъй като показва точно какво еквилайзера ще направи, а не само какво искаме еквилайзера да направи.
Изчисляване на действителния амплитуден спектър
Не е сложно да изчислим действителния амплитуден спектър и да изрисуваме графиката. Даже и ако не знаем нищо друго, можем да използваме груба сила. Вземаме честотата f, създаваме една синусоида sin(2π f k / fs) с тази честота при пробната честота fs и с максимална стойност 1 (което означава средна квадратична амплитуда от 0.707107), пускаме вълната през изчисленията на еквилайзера, изчисляваме средната квадратична амплитуда на получената вълна y(k) и сравняваме двете амплитуди. Нормализирания амплитуден спектър при f тогава ще бъде отношението на амплитудата на изходната вълна и амплитудата на входната вълна f. В децибели, това е
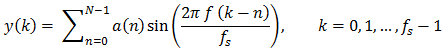
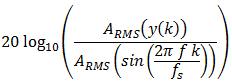
Грубата сила е лесна, но прекалено бавна. Искаме действителния амплитуден спектър (синята линия по-горе) да се променя автоматично, когато потребителя променя амплитудата, честотата, или пък плъзгачите за прецизността на еквилайзера.
Алтернативно, амплитудния спектър на филтъра с ограничен импулсен спектър е честотното съдържание на филтъра с дължина N. Амплитудата при някаква цяла честота f е
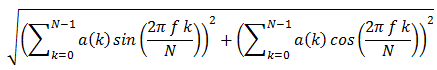
Това изчисление дава средната квадратична амплитуда на изходния сигнал при някаква определена честота и пак трябва да изчислим децибелите. Това изчисление е по-бързо, но можем и да намерим нещо по-добро.
Един филтър a(k) с ограничен импулсен спектър и с дължина N (като нашия еквилайзер), изчислява изхода y(k) от входния сигнал x(k) с формулата
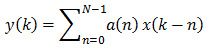
Ако вземем преобразуванието Z на двете страни на това уравнение, ще получим общата форма на трансферната функция на филтъра с ограничен импулсен спектър. Тя е следната.
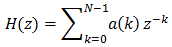
Ако нашият филтър е проектиран правилно, ще бъде сумата на няколко филтри с ограничени импулсни спектри – такива, които пропускат ниски, честоти, високи честоти или честотни ленти – които са симетрични спрямо средата. Тъй като работим с филтри със симетрични коефициенти, можем да съберем първия и последния коефициент, втория и предпоследния коефициент и така нататък. Ще обозначим средата с M = (N – 1) / 2, като предполагаме, че N е нечетно, което обикновено е така. При z = e-j ω, където трябва да изчислим амплитудния спектър
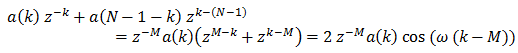
Амплитудният спектър е
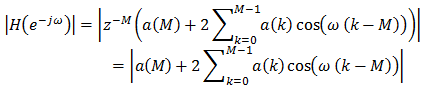
Тук, разбира се, ъгловата честота ω е ω = 2 π f / fs за някаква честота f при някаква пробна честота fs. И пак трябва да превърнем резултата в децибели. Това е, обаче, най-бързия начин да се изчисли амплитудния спектър на филтъра.
автори: mic
Добави нов коментар