Фазов осцилоскоп

Един фазов осцилоскоп, също така наречен "векторскоп", е една графика на стойностите на един сигнал спрямо стойностите на един друг сигнал и показва информация за разликите между амплитудата, фазата и честотното съдържание на двата сигнала.

С други думи, във време t, точката на графиката на фазовия осцилоскоп на двата сигнала x(t) и y(t) е (x(t), y(t)).

Примерни графики, които могат да бъдат произведени от фазовия осцилоскоп, са показани по-долу.

• Разлики в амплитудите на двата сигнала ще разтегнат произведената графика спрямо оста, която съдържа сигнала с по-голяма амплитуда.
• Разлики във фазите на двата сигнала също ще разтегнат произведената графика, но диагонално.
• Разлики в честотите на двата сигнал обикновено ще произведат една по-сложна фигура.

Примери на прости фигури произведени от фазовия осцилоскоп

Когато двата сигнала са прости синусоиди, графиките на фазовия осцилоскоп се наричат криви на Лисажу. Тези криви са прави линии, когато честотите и фазите на двата сигнала са едни и същи. Тъй като синусоидите са периодични, кривите са затворени.

Вземи два прости сигнала във времето x(t) = A sin(a t + d) и y(t) = B sin(b t). По определение, A е амплитудата на сигнала x(t), a е честотата на сигнала x(t) и d е началната фаза на сигнала x(t), B е амплитудата на сигнала y(t) и b е честотата на сигнала y(t). Тъй като фазата на y(t) е нула, d е и разликата в началните фази на двата сигнала.

Да предположим, че A = a = B = b = 1 и d = 0. Когато двете честоти a и b са едни и същи и разликата между фазите е 0, осцилоскопът ще покаже една линия както в следната фигура.

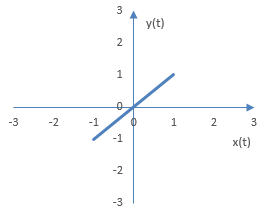
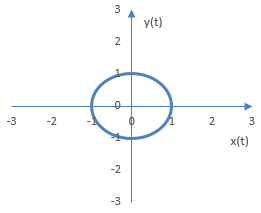
Да предположим пък, че A = a = B = b = 1 и d = π / 2. Когато двете честоти a и b са едни и същи и разликата във фазите не е нула, осцилоскопът ще покаже един кръг (ако разликата във фазите е една четвърт от цикъла на честотата) или елипса.

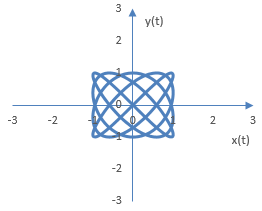
По-сложни графики във фазовия осцилоскоп могат да се произведат ако се вземат две различни честоти. Следното е графиката на фазовия осцилоскоп при A = B = 1, d = 0, a = 4 и b = 5. По-принцип, колко е сложна графиката зависи от отношението a / b.

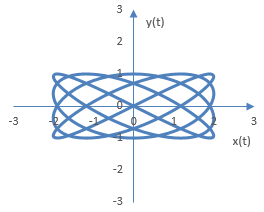
Следното е същата графика, но с A = 2. Ако амплитудата на сигнала x(t) е по-голяма, графиката се разтяга около оста x.

Графики на фазовия осцилоскоп при сложните сигнали

Графиките, които се произвеждат от фазовия осцилоскоп при по-сложните3 сигнали, са по сложни. При работата с аудио, тъй като сигналите се и променят с времето, фигурите може и да не са симетрични.

Следното е една примерна графика на фазовия осцилоскоп, произведена с два сложни сигнала, всеки от които се състои от две синусоиди, с плавно увеличаване на амплитудата в един от сигналите и със случаен шум във втория. Амплитудите, фазите и честотите на двата сигнала са различни.

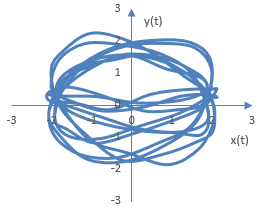
Една графика с фазов осцилоскоп на едно истинско звуково парче е показана в Orinj Фазов осцилоскоп.