admin: First posted on 2013 09 28
This is the third article about deconvolving a reverberated sound to get the impulse response of natural reverberations. If we can do so, then we can use the impulse response as the artificial reverb. In the first post, we created a possible impulse response of a reverb. In the second post, we used the impulse to look at what a drum hit could look like after the reverb. In this article, we will do the opposite. We will try to get the original impulse response, if we assume that we only have the original drum hit and the reverberated drum hit.
The original idea is: we walk into a room that has nice natural reverberations. We record a short sound – a drum hit – reverberated and dry. We compute the impulse response of the natural reverberations from the two signals and we have a nice impulse response that we can use to reverberate anything else. The previous two articles were just the preparation for this article – we created an impulse response and a reverberated drum hit – all for the sake of this article.
In this made-up case
In our made-up artificial case, our job is quite easy. With the convolution y(k) computed as in the picture below (the impulse response a(k) on the left and the drum hit x(k) on the right),
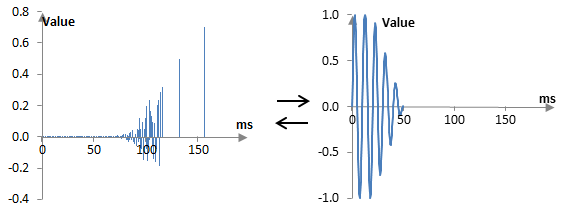
then the first sample of the convolution y(0) is computed only from one sample of the impulse response a(0) and one sample of the drum hit x(0), the second sample of the convolution is computed from two samples of each of the impulse response and the drum hit, and so on. We have
a(0) = y(0) / x(0)
a(1) = (y(1) – a(0) x(0)) / x(1)
a(2) = (y(2) – a(0) x(0) – a(1) x(1)) / x(2)
…
In this made-up case, we can compute the impulse response from the convolution and the drum hit deterministically.
In the real case
In the real case, things are not exactly the same and there are various problems. We may not be able to distinguish between the dry and reverberated signal. We could pick up two microphones, one that is able to pick up the original drum hit and the reverberation and one that would only pick up only the drum hit. However, there is no guarantee that the microphones will pick up the dry signal in the same way as each microphone will add its own coloration to the signal. Also, the second microphone may still pick up some of the reverberated signal, no matter how much we may try to prevent that. The end result is – we cannot quite use the deterministic computation above to get to the impulse response.
Using the original data from the made-up example above, we can add some random errors to the dry drum hit signal to make it slightly different than the drum hit that is contained within the reverberated signal. This would simulate the different coloration of the two microphones. For the example below, the error in each sample on average was about 5% of the original signal (up or down). A deterministic computation produces an impulse (red below) that is almost the same as the original (blue), although, obviously, slightly different.
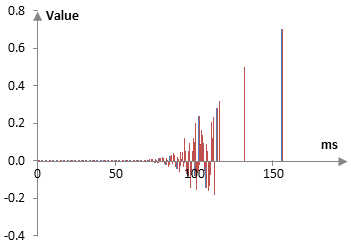
Since now in the deterministic computation above not many of the samples compute to zero as would have happened with a clean signal without the random errors, we have a lot more nonzero samples in the impulse.
As an alternative to the deterministic deconvolution, we could use optimization. The idea would be to find the impulse response that, when applied to the original signal, produces a signal that is as close to the reverberated signal as possible. If we try to do so, we may get an impulse response that is quite ugly.
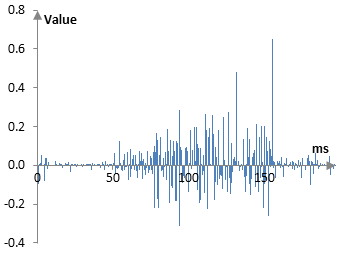
Is that the right response or is the deterministic one above better? The deterministic deconvolution produces an impulse response that looks closer to the original one, but that shouldn't matter. What is important is that both impulse responses produce a reverberated signal that is close (almost the same) to the "natural" reverberated signal that we produced in the previous article.
There is, of course, a choice with the optimization. We can optimize an impulse or we can optimize a collection of Shroeder all pass and comb filters. There is also a problem with the optimization as set up here. The drum signal is too "clean". In this unrealistic example, the drum hit is a simple sine wave. This is perhaps why the resulting optimized impulse response contains so much "noise". Two notches that are next to each other, for example, will produce a result that is almost the same as a single notch with twice the size. In a realistic example, this, perhaps, will not happen. A realistic signal should contain a large number of frequencies.
authors: mic
Comments
Impulse response of natural reverb
Can't fine part 4.
Also, what seems significant is that an impluse response of a strict digital early, late and reverb will show all positive vertical lines, with a variation in timing and level but that is all. What we see with impulse response of natural reverb is a series of positive and negative lines randomized variation in timing and level. So, discrete time delay (corrolated) version of reverberation may well not sound the same as natural (decorrolated) reverberation. I'm remembering teaching a class where we compare the digital delay version of "reveberation" developed in an outdoors wood lot vs the reverberation developed inside a metal barn. They sound greatly different.
Possibly some subjective impressions of corrloated vs decorrolated reverberation would be useful?
Yes (except I don't
Yes (except I don't understand the comment on positive vs. negative reflections). In princple, decorrelation is often the goal. At least when I work with reverbs, it is rare that I like the opposite. But, as you hinted, that is hard to achieve with small computational powers. Thanks.
This article was a very simplistic experiment. It is not the right deconvolution. It was just meant to present an easy to understand example.
There is no part 4. I was working with various digitally designed reverbs and I moved to actual deconvolution (in the frequency domain), but that was beyond what I wanted to write about here.
Add new comment