In digital signal processing, aliasing occurs when the signal is not sampled with a high enough sampling rate and consequently high frequencies are confused with low frequencies.
According to the Nyquist-Shannon sampling theorem, the sampling rate fs can properly represent frequencies of only up to fs / 2. Since
$$\sin(\frac{2\pi(f_s-f)k}{f_s})=\sin(-\frac{2\pi f k}{f_s}+2\pi k)=-\sin(\frac{2\pi f k}{f_s})$$
the frequencies f and fs – f, if sampled with the frequency fs, would have the same values at all samples. Thus, even though we may be sampling the higher of those two frequencies, any equipment or software would confuse this higher frequency for the lower one.
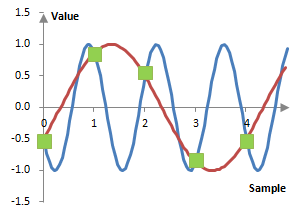
The following figure shows the waves f = 500 Hz and fs – f = 1500 Hz sampled at fs = 2000 Hz. Both waves have the same values at each sample.
Add new comment