The Chebychev filter of type II is given by the normalized transfer function
$$H(S)=\epsilon \prod_{k=1}^{n} (S-r_k) \prod_{k=1}^{n} \frac{1}{S-s_k}$$
where n is the order of the filter, ε defines the size of the ripples of the filter's magnitude response in the stop band, the roots of the numerator rk are
$$r_k=\frac{1}{-j \, \cos(\frac{\pi (2k-1)}{2n})}$$
and the roots of the denominator sk are
$$s_k=\frac{1}{-\sinh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{n}) \, \sin(\frac{\pi (2k-1)}{2n})+j\,\cosh(\frac{\mathrm{asinh}(\frac{1}{\epsilon})}{n}) \, \cos(\frac{\pi (2k-1)}{2n})}$$
Here sinh and cosh are the hyperbolic sine and cosine functions and asinh and acosh are the inverse hyperbolic sine and cosine functions.
The transfer function above is shown irrespective of the cutoff frequency (i.e., it is normalized for the cutoff frequency 1) and the forms of the Chebychev type II filter require substitutions. Use S = s / ωc to get the Chebychev type II low pass filter, where s = jω, ωc is the cutoff frequency of the filter, and ω is the angular frequency spanning the frequency spectrum between 0 and π. Use S = ωc / s to get the Chebychev type II high pass filter. Use S = (s2 + ωc2) / (B s) to get the Chebychev type II band pass filter, where ωc is the midpoint of the pass band and B is the width of the band. Use S = B s / (s2 + ωc2) to get the Chebychev type II band stop filter.
This filter is also called the "inverse Chebychev filter". Its poles (the roots of the denominator) are the inverse of the Chebychev filter of type I and as its gain function (shown below) "inverts" the gain function of the Chebychev filter of type I. While the Chebychev filter of type I controls the size of ripples in the pass band, this filter exhibits a flat pass band and controls the size of the ripples in the stop band.
Example: Fourth order low pass Chebychev type II filter
Set n = 4 and use the substitution S = s / ωc. The transfer function of the fourth order low pass Chebychev type II filter is
$$H(s)=\frac{\epsilon (s-r_1\omega_c) (s-r_2\omega_c) (s-r_3\omega_c) (s-r_4\omega_c)}{(s-s_1\omega_c) (s-s_2\omega_c) (s-s_3\omega_c) (s-s_4\omega_c)}$$
Note that r1 and r4 are complex conjugates, r2 and r3 are complex conjugates, s1 and s4 are complex conjugates, and s2 and s3 are complex conjugates. Moreover, the roots of the numerator rk have real parts equal to zero, and hence r1 + r4 = 0, and r3 + r2 = 0. To make our computations easier, we can rewrite the transfer function as follows.
$$H(s)=\frac{\epsilon (s^2+r_1 r_4 \omega_c^2) (s^2+r_2 r_3 \omega_c^2)}{(s^2-(s_1+s_4)\omega_c+s_1 s_4 \omega_c^2)(s^2-(s_2+s_3)\omega_c+s_2 s_3 \omega_c^2)}$$
or
$$H(s)=\frac{\epsilon (s^4+A s^2 + B)}{s^4+C s^3+D s^2+E s + F}$$ $$A=\omega_c^2 (r_1 r_4 + r_2 r_3)$$ $$B=\omega_c^4 r_1 r_4 r_2 r_3$$ $$C=-\omega_c (s_1+s_4+s_2+s_3)$$ $$D=\omega_c^2 (s_1 s_4+s_2 s_3+(s_1 + s_4)(s_2+s_3))$$ $$E=-\omega_c^3 (s_1 s_4 (s_2+s_3) +s_2 s_3 (s_1 + s_4))$$ $$F=\omega_c^4 s_1 s_4 s_2 s_3$$
After the bilinear transformation s = 2 (z – 1) / (z + 1) the transfer function becomes a Z transform transfer function.
$$H(z)=\frac{a_0+a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}+a_4 z^{-4}}{b_0+b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}+b_4 z^{-4}}$$ $$a_0=a_4=\epsilon (16+4 A+B)$$ $$a_1=a_3=\epsilon (-64+4B)$$ $$a_2=\epsilon (96-8A+6B)$$ $$b_0=16+8C+4D+2E+F$$ $$b_1=-64-16C+4E+4F$$ $$b_2=96-8D+6F$$ $$b_3=-64+16C-4E+4F$$ $$b_4=16-8C+4D-2E+F$$
Say that the cutoff frequency of the filter is ωc = 0.6 and that ε = 0.1 (technically, the cutoff frequency of the filter will be ωc = 2 arctan(0.6/2) ≈ 0.583, due to the warping of the frequency domain by the bilinear transformation). The transfer function of this example Chebychev type 1 low pass filter, after scaling to obtain b0 = 1 is
$$H(z)=\frac{0.090729-0.190160z^{-1}+0.251568z^{-2}-0.190160z^{-3}+0.090729z^{-4}}{1-2.662409z^{-1}+2.828952z^{-2}-1.378102z^{-3}+0.264003z^{-4}}$$
and the filter itself is
$$y(k) = 0.090729 x(k) – 0.190160 x(k – 1) + 0.251568 x(k – 2)$$ $$– 0.190160 x(k – 3) + 0.090729 x(k – 4) + 2.662409 y(k – 1) $$ $$– 2.828952 y(k-2) + 1.378102 y(k – 3) – 0.264003 y(k – 4)$$
Suppose that the sampling frequency is 2000 Hz. The cutoff frequency then is ωc = (0.6 * 2000) / (2 π) = 191 Hz. The magnitude response of the filter is shown in the graph below.
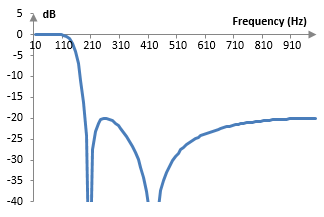
Size of the ripples in the stop band
The magnitude function of the Chebychev type II low pass filter can also be written as follows.
$$|H(j\omega)|=\frac{1}{\sqrt{1+\frac{1}{\epsilon^2 T_n^2 (\frac{\omega_c}{\omega})}}}$$
where Tn are the Chebychev polynomials
$$T_n(x)=\begin{cases} \cos(n\,\mathrm{acos}(x)) & |x|\le1 \\ \cosh(n\, \mathrm{acosh}(x)) & |x| \gt 1 \end{cases}$$
In the stop band, where ωc / ω < 1, Tn(ωc / ω) = \cos(n \mathrm{acos}(ωc / ω)) and 0 ≤ Tn2(ωc / ω) ≤ 1. In the stop band
$$0 \lt |H(j\omega)| \le \frac{1}{\sqrt{1+\frac{1}{\epsilon^2}}}$$
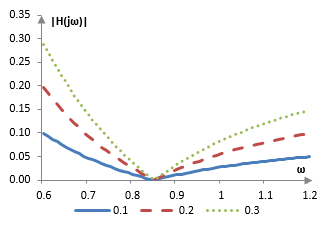
Thus, smaller ε implies smaller ripples in the stop band and larger ε implies larger ripples. It should also be expected that |H(jω)| approaches 0 at ωc / ω approaches cos(π / 2n), since then Tn(ωc / ω) = 0.
Using the same parameters as above, namely n = 2 and ωc = 0.6, we can plot the |H(jω)| for three different values of ε (0.1, 0.2, and 0.3).
The magnitude response of the three corresponding filters is:
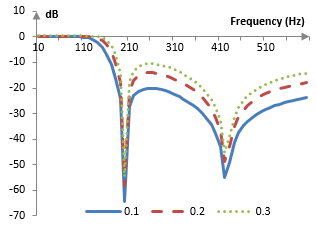
A larger ε creates a filter with a smaller transition band, but with larger ripples in the stop band and worse stop band attenuation. A smaller ε creates a filter with smaller ripples in the stop band and better stop band attenuation, but with larger transition band.
Example: Second order band stop Chebychev type II filter
Set n = 2 and S = B s / (s2 + ωc2). The transfer function of the second order band stop Chebychev type II filter is
$$H(s)=\epsilon \frac{B^2 s^2+r_1 r_2(s^2+\omega_c^2)^2}{B^2 s^2-B(s_1+s_2)(s^2+\omega_c^2)s+s_1 s_2(s^2+\omega_c^2)^2}$$
s1, s2, r1 and r2 are computed with the same formulae as before. After the bilinear transformation s = 2 (z – 1) / (z + 1), setting, for example, ε = 0.1, B = 0.5 and ωc = 0.8, and scaling to obtain 1 at the beginning of the denominator, we have the following band stop transfer function
$$H(z)= \frac{0.532250-1.506697z^{-1}+2.107234z^{-2}-1.506697z^{-3}+0.532250z^{-4}}{1+1.933150z^{-1}-1.879211z^{-2}+1.065289z^{-3}-0.276782z^{-4}}$$
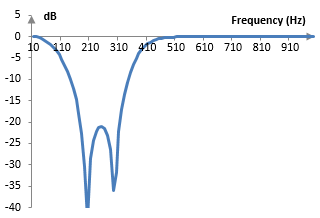
If we suppose that the sampling frequency is 2000 Hz, then ωc = (0.8 * 2000) / (2 π) = 255 Hz, B = (0.5 * 2000) / (2 π) = 159 Hz, and the magnitude response of the filter is as follows.
Higher order Chebychev type II filters
Higher order Chebychev type II filters can be designed either using the methods above, or by stacking lower order filters. For example, the transfer function for the fourth order low pass Chebychev type II filter could have also been written as
$$H(s)= \epsilon \frac{(s-r_1\omega_c)(s-r_4\omega_c)}{(s-s_1\omega_c)(s-s_4\omega_c)} \frac{(s-r_2\omega_c)(s-r_3\omega_c)}{(s-s_2\omega_c)(s-s_3\omega_c)}$$
This means that the fourth order low pass Chebychev type II filter can be implemented by stacking two filters of order two (these are not Chebychev type II filters, as the roots of each filter of order two differ from the Chebychev roots). Multiplying two transfer functions means that the impulse response of the total filter is the convolution of the two impulse responses of the lower order filters and the output of the first filter is the input to the second filter. We combine the roots in the manner above, as s1 and s4, s2 and s3, r1 and r4, and r2 and r3 form complex conjugate pairs. It is not important whether ε is used in the first filter, the second filter, or split between the two.
The following is a comparison of the magnitude responses of the fourth order and second order Chebychef type II filters with ε = 0.1, sampling frequency of 2000 Hz, and ωc = 0.6.
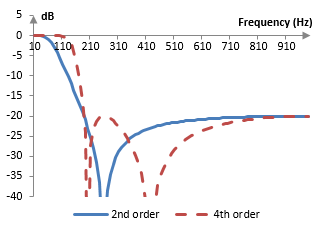
Odd order Chebychev type II filters
When the Chebychev type II filter is of odd order n, one of the roots rk of the numerator cannot be computed, as the computation produces a division by zero. At k = (n – 1) / 2 we have rk = 1 / (-j cos(π / 2)). Thus, when n is odd, the middle root of the numerator is omitted from the transfer function, and the numerator becomes a polynomial of s of a lower degree than the denominator. Take, for example, the low pass Chebychev type II filter of order n = 3. Its transfer function, after omitting the middle root r2, is as follows.
$$H(s)= \epsilon \frac{(s-r_1\omega_c)(s-r_3\omega_c)}{(s-s_1\omega_c)(s-s_2\omega_c)(s-s_3\omega_c)}$$
Since r1 and r3 are complex conjugates, s1 and s3 are complex conjugates, and s2 is a real number, we can rewrite the transfer function above as a function with real coefficients in the following way.
$$H(s)= \frac{\epsilon (s^2+r_1 r_3 \omega_c^2)}{s^3-(s_1+s_3+s_2)\omega_c s^2+(s_1 s_3+(s_1+s_3)s_2)\omega_c^2 s-s_1 s_3 s_2 \omega_c^3}$$
After the bilinear transformation this filter has the transfer function
$$H(z)= \frac{a_0+a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}}{b_0+b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}}$$ $$a_0=a_3=\epsilon(4+r_1 r_3 \omega_c^2)$$ $$a_1=a_2=\epsilon(-4+3 r_1 r_3 \omega_c^2)$$ $$b_0=8-4(s_1+s_3+s_2)\omega_c+2(s_1 s_3+(s_1+s_3)s_2)\omega_c^2-s_1 s_3 s_2\omega_c^3$$ $$b_1=-24+4(s_1+s_3+s_2)\omega_c+2(s_1 s_3+(s_1+s_3)s_2)\omega_c^2-3 s_1 s_3 s_2\omega_c^3$$ $$b_2=24+4(s_1+s_3+s_2)\omega_c-2(s_1 s_3+(s_1+s_3)s_2)\omega_c^2-3 s_1 s_3 s_2\omega_c^3$$ $$b_3=-8-4(s_1+s_3+s_2)\omega_c-2(s_1 s_3+(s_1+s_3)s_2)\omega_c^2-s_1 s_3 s_2\omega_c^3$$
For example, when ωc = 0.6 and after scaling to obtain b0 = 1 in the denominator, the filter would be
$$H(z)=\frac{0.0369-0.0211z^{-1}-0.0211z^{-2}+0.0369z^{-3}}{1-2.179z^{-1}+1.666z^{-2}-0.431z^{-3}}$$
This filter, however, produces a magnitude response in the pass band of about -5 dB. To ensure that the filter does not attenuate the pass band, we add some gain by scaling the coefficients in the numerator, so that H(s), evaluated at zero, is equal to 1. The gain is
$$\frac{1}{|H(0)|}=\frac{s_1 s_3 s_2 \omega_c^3}{\epsilon r_1 r_3 \omega_c^2}$$
In the example above the gain is 1.8 and the filter itself changes to
$$H(z)=\frac{0.0665-0.0380z^{-1}-0.0380z^{-2}+0.0665z^{-3}}{1-2.179z^{-1}+1.666z^{-2}-0.431z^{-3}}$$
The magnitude response of this third order filter is shown below with the magnitude responses of two Chebychev type II filter so order 2 and 4.
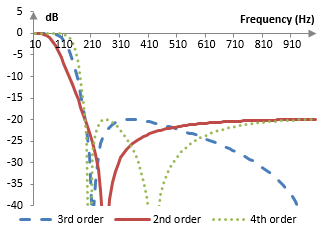
Comments
Older comments
admin: First posted on 2011 12 01
Werner Van Belle, 2011 12 01: Very nice summary. I found it remarkably hard to find the correct transfer function for the type 2 filter. So, everything is working out quite well now, except for the odd orders. What does one do with the middle zero ? This gives an expression (s+infinity*j)
mic, 2011 12 03: Yes. When the order of the filter is odd, one of the zeroes of the numerator becomes "infinite" (results in a division by zero). From what I have seen, this zero is simply removed from the numerator. This means that the (s + j * infinity) that you mentioned is not included in the numerator. The numerator becomes a polynomial of lower order than the polynomial in the denominator.
mic, 2011 12 17: We added an example of an odd order Chebychev type II computations. When the middle root of the numerator is dropped, the gain of the filter should be adjusted as described above.
Add new comment