A high pass filter is a frequency filter that allows (passes) frequency above a certain cutoff frequency and disallows (stops) the frequencies below that cutoff frequency.
Example high pass filter and sound sample
See Orinj High pass filter to hear a sound sample before and after a high pass filter.
Ideal magnitude response of a high pass filter
The following is a graph of the ideal magnitude response of a high pass filter.
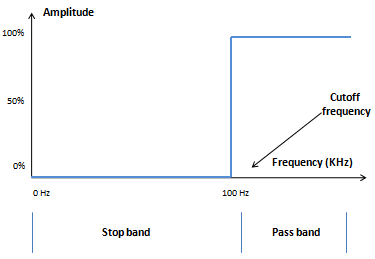
All frequencies above the cutoff frequency remain at their original amplitude. All frequencies below the cutoff frequency are completely removed.
Using high pass filters in music production
High pass filters are very common in music production. They can be used to separate instruments in the frequency spectrum (i.e., to ensure that different instruments occupy mostly different parts of the frequency spectrum). For example, a high pass filter with a cutoff frequency of about 300 Hz or higher over a guitar track can help separate the guitar from the bass. This filter will remove the frequencies in the bass range from the guitar. High pass filters with higher cutoff frequencies can separate similarly two guitars or any other instruments.
A high pass filter with a very low cutoff frequency (e.g., 40 Hz) can be used to remove low frequencies from the bass and, perhaps, kick to prevent muddiness and ear fatigue in the mix.
Example: Digital filter with finite impulse response
Consider a filter w(k) that takes the incoming signal x(n) and computes the output signal y(n) with the formula
$$y(n)=\sum_{k=0}^{N} w(k)\,x(n-N+k)$$
with weights defined according to the following formula.
$$w(k)=\begin{cases} -\frac{\sin(2\pi \frac{f}{f_s}(k-\frac{N-1}{2}))}{\pi (k-\frac{N-1}{2})}, k \ne \frac{N-1}{2} \\ 1-2\frac{f}{f_s}, k=\frac{N-1}{2} \end{cases}$$
Here fs is the sampling frequency, N is the length of the filter (the number of items in the weighted sum), w(k) are the filter weights, and f is some frequency between 0 and fs / 2. This filter is a high pass filter with a cutoff frequency f as it allows frequencies above f to pass and as it attenuates frequencies below f.
If, for example, fs = 2000 Hz, f = 40 Hz, and N = 201, the magnitude response of the filter will be as in the graph below.
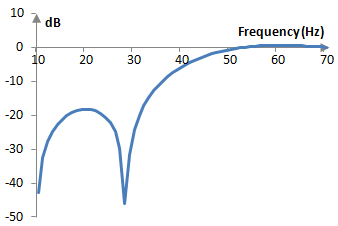
While the magnitude response of this filter is not ideal, this filter passes frequencies above 40 Hz almost unchanged and attenuates frequencies below 40 Hz. It is thus a high pass filter with a cutoff frequency of 40 Hz.
The differences between this filter and an ideal filter are several.
- The frequencies that should be stopped are not completely stopped. In this frequency band – the stop band – there is some stop-band attenuation, but it is only about -20 dB.
- In the stop band and in the pass band, the magnitude response is not flat, but there are ripples (see Gibbs phenomenon).
- The magnitude response of this filter does not transition between the stop band and the pass band immediately but does so gradually. There is thus a transition band of frequencies.
If the length of this filter is increased, its stop band attenuation improves, the transition band decreases (the transition is faster), and the size of the ripples decrease.
Deriving the finite impulse response high pass filter
The high pass filter above can be derived by inverting a low pass filter.
- See Low pass filter for an explanation about how to derive a finite impulse response low pass filter.
- We recognize that a finite impulse response low pass filter with coefficients that are symmetric around the middle, such as this low pass filter, will introduce a constant delay in the phase of frequencies in the signal (see Phase response).
- We design an all pass filter that passes all frequencies with unchanged magnitude, but that is also a finite impulse response filter with coefficients that are symmetric around the middle. This filter will introduce the same phase delay as the low pass filter. The all pass filter is 0, 0 …, 0, 1, 0, 0, …, 0, with length equal to the length of the low pass filter.
- We subtract the output of the low pass filter from the all pass filter. The all pass filter passes all frequencies. The low pass filter passes low frequencies. The difference is the high frequencies. This only works because the phase delay is the same in both filters.
- We also note that, since the computation of the filters over the signal is linear, rather than subtracting the outputs of the filters, we can subtract the filter coefficients.
The result is the filter shown above.
Infinite impulse response high pass filters
Examples of infinite impulse response high pass filters are shown in the topics Bessel filter. Butterworth filter, Chebychev filter (Type I), Elliptic filter.
Add new comment