I noticed a Twitter post the other day about dynamics processing of signals with DC gain. I didn't think DC gain matters, because a compressor does not care whether the signal is symmetrical. It attacks both sides of the signal with the same compression gain.
It turns out that DC gain matters, but not much.
A simple sine wave with DC gain
Here is a simple sine wave with some DC gain. This sine wave is the frequency 200 Hz sampled at 44.1 kHz. The horizontal axis shows the first 300 samples. The vertical axis shows the amplitude of the wave.
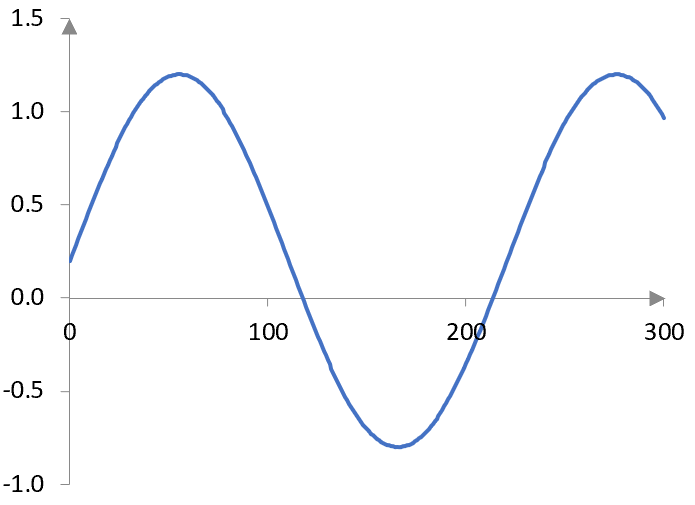
The additional DC gain is 0.2. The wave is not symmetrical around the horizontal axis. There is more of the wave on top then there is at the bottom and the wave oscillates between -0.8 and 1.2. A symmetrical wave – one without the DC gain – would have oscillated between -1 and 1.
Detecting the amplitude of this wave
A compressor needs to know the amplitude of the wave so that it can, potentially, adjust it.
We put this sine wave through the amplitude detection of a compressor (through a Hilbert transform with some additional computations).
Here is the resulting amplitude. The horizontal axis, again, shows the samples, but we have removed the sample numbers as the Hilbert transform shifts the signal and so the sample numbers would be confusing.
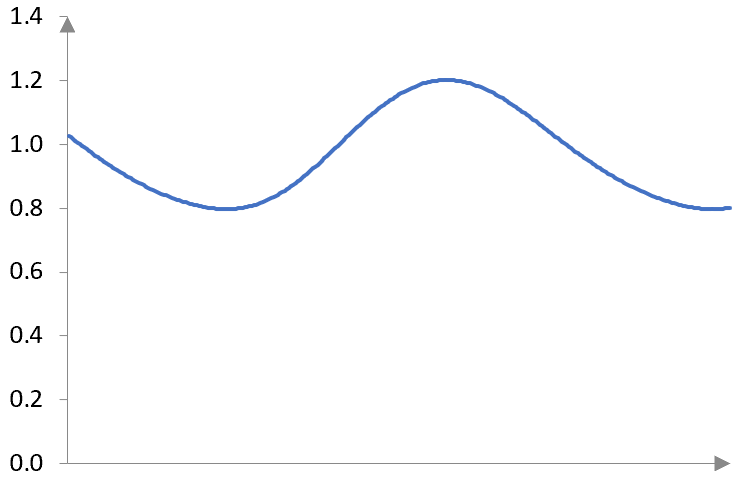
We expect the amplitude to be constant, since this is just a simple sine wave. However, the amplitude oscillates.
In contrast, here is the amplitude, as detected by the same compressor, of a simple sine wave without any extra DC gain.
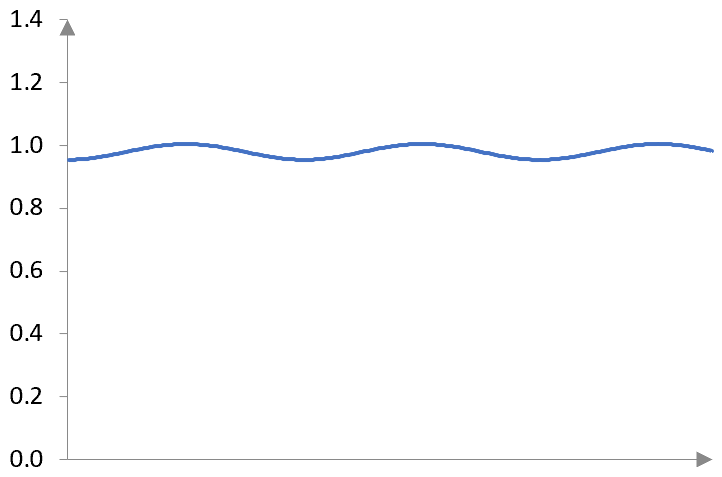
The amplitude of a simple sine wave, as detected by our compressor, is more or less constant. It still oscillates (the Hilbert transform is not perfect), but a lot less when there is DC gain.
What does all this mean?
What does all this mean? Not much, actually.
The detected amplitude oscillates at the same rate as the original wave. That rate is 200 Hz or once per 5 milliseconds. Perhaps we should be worried about compressors that act too quickly. If the compressor adjust the gain faster than the movement of the wave itself, it would introduce distortion.
However, most compressors act much slower. Even with very fast compression attack, there is still the compression release. Thus, while the oscillation of the gain may, depending on the compression threshold, push the compressor to continuously switch between attack and release, the gain changes introduced by the compressor would still not move fast enough to distort the signal.
Moreover, this is 200 Hz. At higher frequencies, distortion is even less likely.
Finally, a compressor can always be designed to adjust for DC gain. It is easy to do.
Of course, it remains to be seen what happens when we have a more complex signal with DC. Maybe DC matters more then.
authors: mic
Comments
This is just a piece of the puzzle
I just realized that this a very small piece of the puzzle. There are various reasons why a complex signal might be asymmetric. DC is just one. How underlying frequencies with their phases interact is another. The fact that some recordings, like vocals, are asymmetric simply because we always have to breathe out when singing is another. DC tends to be constant, which makes easiest to address. The other reasons are not and addressing those is much more complex (e.g., phase rotators). I suppose I'll take a look at those at some point.
Add new comment