The Shroeder reverb is a way to simulate late reverberation in digitally recorded audio.
When modeling natural reverberation, we normally distinguish between the early reflections of the sound (usually the first 100 ms), which may be few and more distinct, and late reverb or reverb tail, which may contain more reflections of the sound that are indistinguishable from each other. Early reflections are modeled with a tapped delay line (see Reverb). The Shroeder reverb is one way to model the late reverb.
The Shroeder reverb is a sequence of Shroeder all pass filters, followed by several parallel feedforward comb filters as in the graph below.
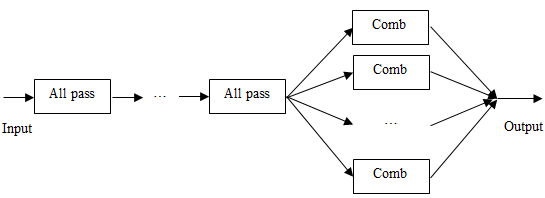
The Shroeder all pass filters use the following computations
$$y(k)=g\,x(k)+x(k-n)-g\,y(k-n)$$
or, in other words, the transfer function
$$H(z)=\frac{g+z^{-n}}{1+g\,z^{-n}}$$
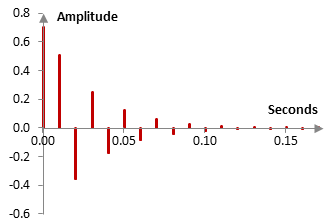
where x(k) is the input signal at sample k, y(k) is the output signal at sample k, g is some gain, typically set around 0.7 as discussed below, and n is some delay in number of samples (see All pass filter to verify that this is an all pass filter). For example, an all pass filter with g = 0.7 and n = 20 samples, when the sampling frequency is 2000 Hz (n = 20 translates to a delay of 10 ms), results in the impulse response shown on the following figure.
Generally, the all pass filters in the Shroeder reverb use very short delays – between 3-35 milliseconds. Their purpose is to simply produce many repetitions of the signal with decaying amplitude. The feedforward comb filters in the Shroeder reverb have larger delays that the all pass filters – between 100 and 150 milliseconds. They introduce irregularities – peaks – in the reverb. These irregularities are something that Shroeder noted existed in natural reverbs (Shroeder noted about 15 peaks).
Consider the impulse response in the figure below. Two successive all pass filters create the multitude of repetitions in red. One single feedforward comb filter that takes the all pass filters' output would contain both the impulses in red, but will also create a repetition of the pattern, in blue.
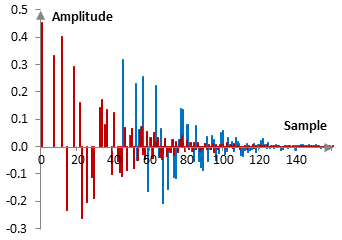
In the figure above, the all pass filters have feedback gains of 0.7 and 0.65 and delays of 7 and 11 samples respectively (the sampling frequency in the example is 2000 Hz). The comb filter uses a gain of 0.7 and delay of 45 samples. These parameters are, of course, somewhat random. Properly chosen parameters should depend on the sampling rate, the desired total reverb length, the amount of reverb diffusion, and other. Fine-tuned examples of Shroeder reverb implementations are widely available.
Shroeder made recommendations – ones that we can use to tune the Shroeder reverb – including, for example, that all filters use varying delays of approximately
$$\frac{100 \, ms}{3^k}, \,\,\, k=0, 1, 2, ...$$
This recommendation translates to having comb filters with delays of about 100 ms and all pass filters with delays at approximately 33 ms, 11 ms, 3 ms, etc. In order for the delayed repetitions to not coincide often, rather than choosing delays that are precisely equal to those values, reverb designers typically choose delays in number of samples that are mutually prime. For example, when sampling at 2000 Hz, three successive all pass filters could use delays of 7, 23 and 67 samples, since these numbers are mutually prime and correspond to approximately 3 ms, 11 ms, and 33 ms.
Similarly, if comb filters typically use delays of 100 ms, the delays expressed as number of samples are also chosen to be mutually prime and typically mutually prime with the all pass delays. At 2000 Hz, for example, appropriate delays for four comb filters could be created with 211, 223, 239, and 263 samples.
The gains in all filters are usually set between 0.5 and 0.7. This said, the gain is an important control parameter, as it affects the total length of the reverb. For example, an all pass filter with delay of t milliseconds will become silent – will drop to -60 dB – in
$$t \log_g(10^{-\frac{60}{20}})$$
milliseconds. Thus, the all pass filter with the largest delay at 33 ms, with g = 0.7 will quiet down after approximately 640 ms, or a bit over half a second. If the output of this all pass filter is repeated with the feedforward comb filter at 150 ms, then we have a late reverb of approximately 800 ms. The same number with g = 0.5 would be about 470 ms.
Add new comment