Sine sweep

A sine sweep is a sine function that gradually changes frequency over time.

The sine sweep can also be called "sinusoidal sweep," "frequency sweep", or "chirp".

The functions

$$x(t)=\sin(2\,\pi(f_0\, t+\frac{f_1-f_0}{2\,T}t^2))$$

and

$$x(t)=\sin(2\,\pi\,f_0 \,T \frac{(\frac{f_1}{f_0})^{\frac{t}{T}}-1}{\ln(\frac{f_1}{f_0})})$$

for example, change frequency from f₀ to f₁ over the time T. The first function is called a linear sine sweep, as the derivative of the frequency term inside the sine with respect to the time t is linear. Similarly, the second function is an exponential sine sweep.

Both functions have an initial phase of zero. A different initial phase can be added as with any other sine function, if necessary. In both functions, replacing t with k / f_s, where k = 0, 1, 2, … and f_s is the sampling frequency produces the discrete time equivalent of the functions.

Example sine sweep

The following is an exponential sine sweep that changes frequency from 1 Hz to 50 Hz over 2 seconds.

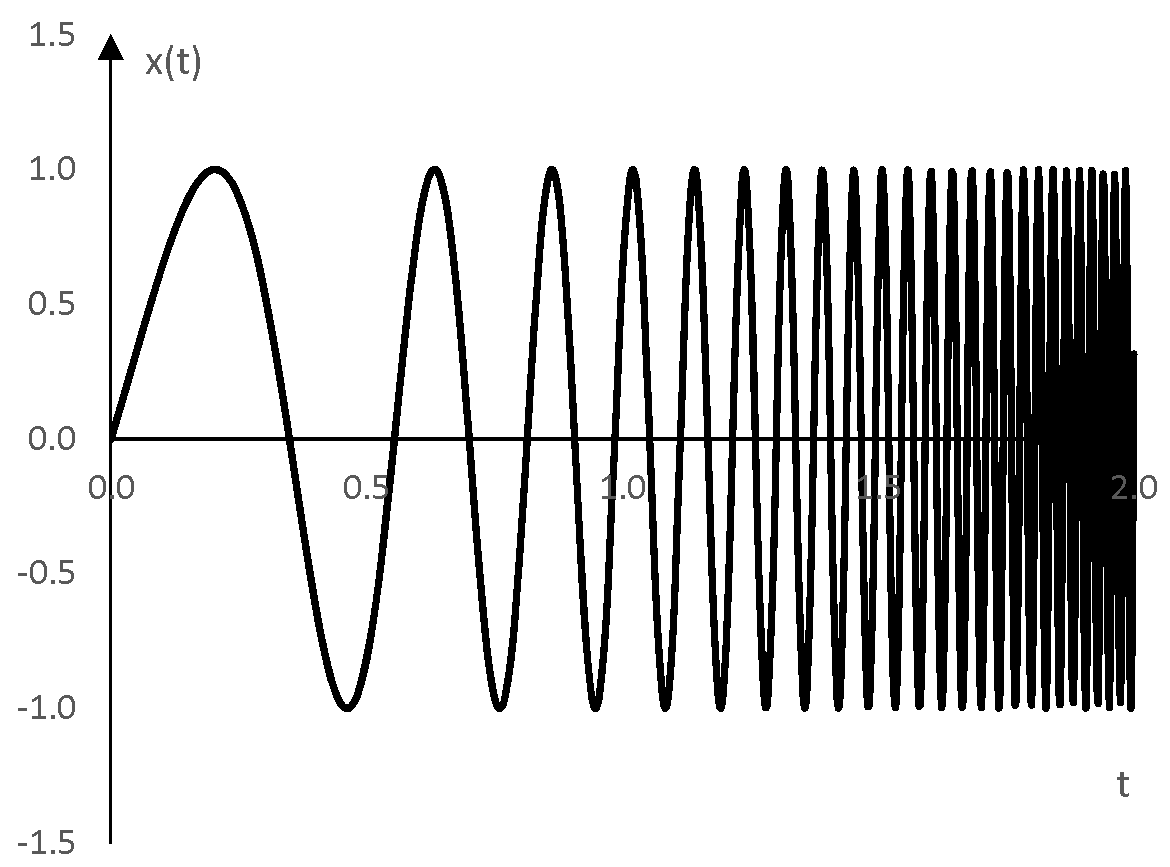
Sine sweep sound

The following is a linear sine sweep, generated with the formula above, where the beginning frequency f₀ is 50 Hz, the end frequency is f₁ is 1000 Hz, and the time T is 1 second.

Click Play to hear the linear sine sweep.

The following is an exponential sine sweep with the same parameters – sweeping the frequencies between 50 Hz and 1000 Hz over 1 second.

Click Play to hear the exponential sine sweep.

Using the sine sweep

Sine sweeps are useful when obtaining the impulse response of natural reverberations to design an impulse reverb. In practice, one can play a sine sweep in a room, record the result, and deconvolve the result with the sine sweep inverted in time to obtain the impulse of the reverb.

An example of this is below. Typically, a sine sweep used for this purpose will span the full possible frequency spectrum (e.g., from 20 Hz to 22 kHz for the full spectrum of human hearing and to cover the maximum possible under the 44.1 kHz sampling rate). Recommendations for how long the sine sweep should be vary, but are usually between 3 seconds to 20 seconds. For ease of presentation, the example below uses a shorter sine sweep that does not span the full frequency spectrum.

Take the following impulse response a(t).

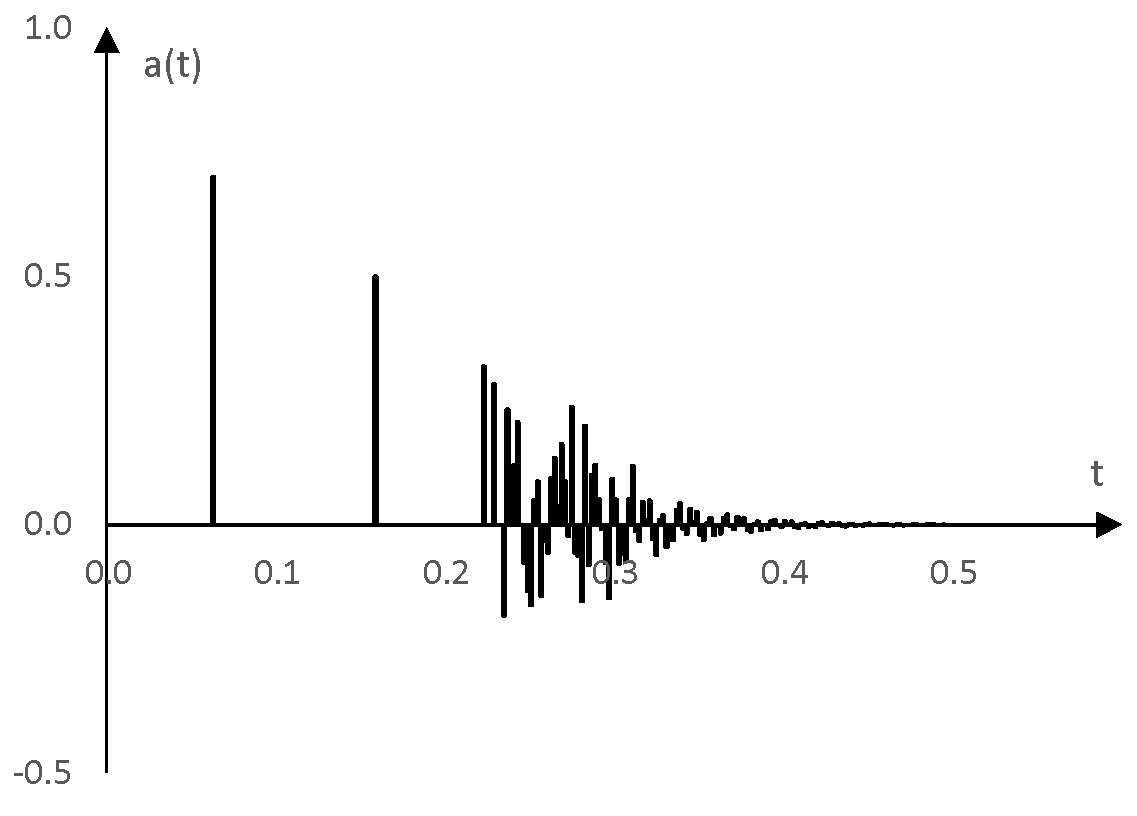
This graph imitates the impulse response of some reverb. It was produced by running an impulse through a feedforward comb filter and running the output of the comb filter through a Shroeder all pass filter (see All pass filter). This is a 300-point impulse response over the sampling frequency 500 Hz.

Convolve this impulse response with an exponential sine sweep between 1 Hz and 200 Hz. The convolution h(t), which by itself is not very interesting, is as follows.

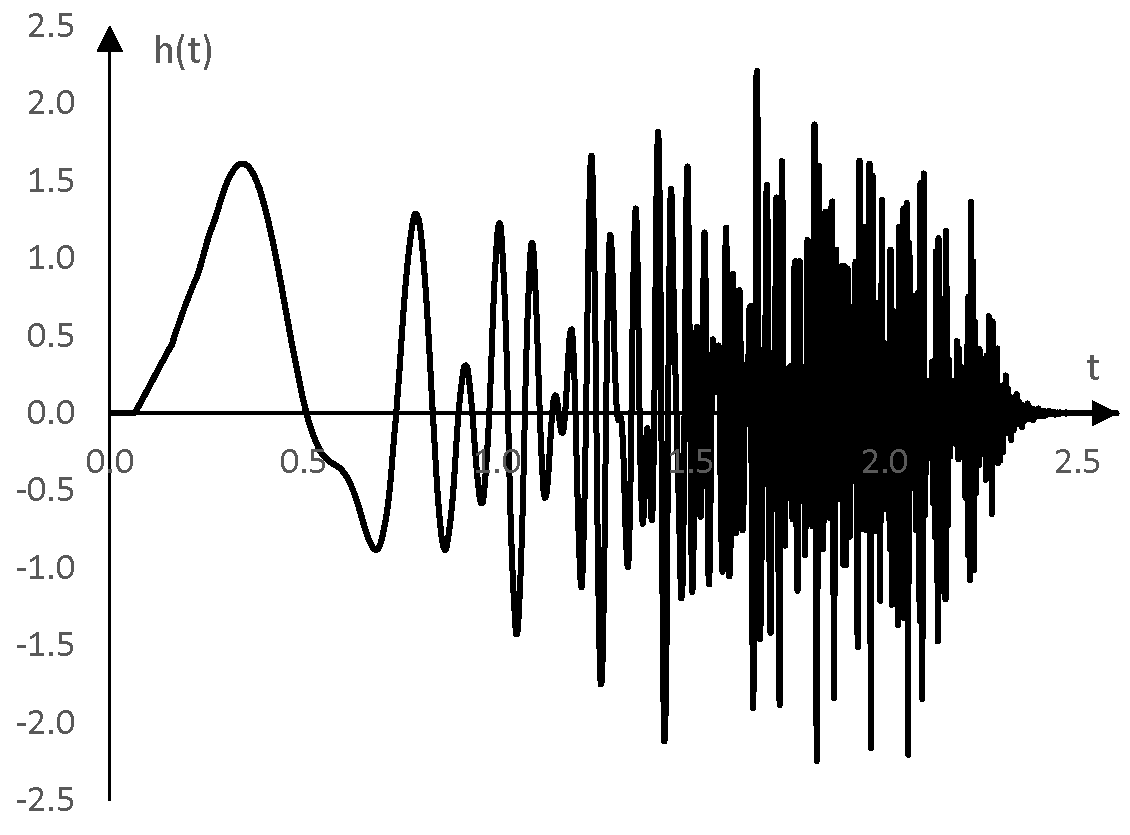
In practice, when recording natural reverberations of a sine sweep, we will have this result and we will know the sine sweep employed, but we will not know the impulse response. To get the impulse response, we can convolve this result with the same sine sweep but inverted in time. If we do so in this example, we will get the following impulse response.

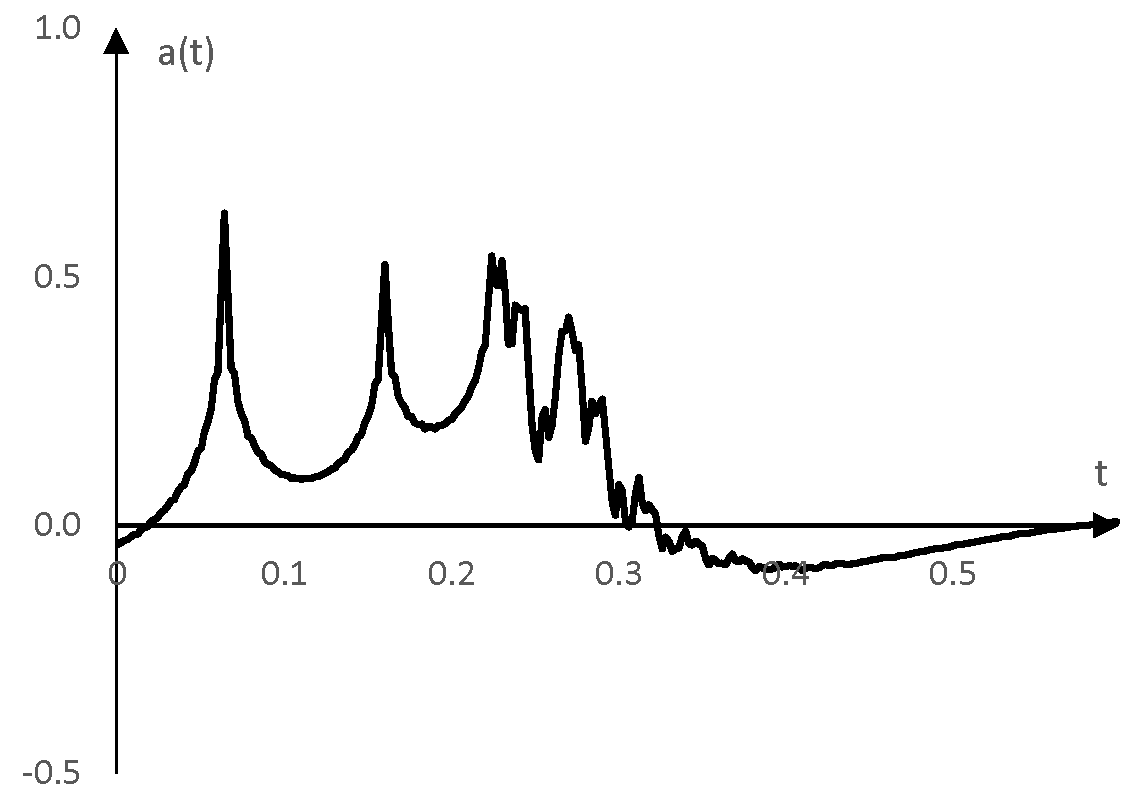
This impulse response is quite close to the initial impulse response.

There is, however, a good amount of "pre-ringing". This generated impulse response does not jump quickly from zero to the peak of the first notch but does that gradually.

The technique to reduce this pre-ringing is to deconvolve with the time inverted sine sweep with an adjusted amplitude. We reduce the gain of the frequencies in the sine sweep by 6 dB per octave. The gain will be 0 dB (no change) at the high frequency end of the sine sweep and will gradually decrease to

$$-6 \, \log_2 \frac{f_1}{f_0}$$

at the low frequency end. In the current example, since frequencies in the sine sweep change from 1 Hz to 200 Hz, the amplitude over the sine sweep will gradually, linearly change from 0 dB at 200 Hz to -46 dB at 1 Hz.

The new impulse response, after adjusting the amplitude of the sine sweep used in the deconvolution (and after we add some gain to the result), is below.

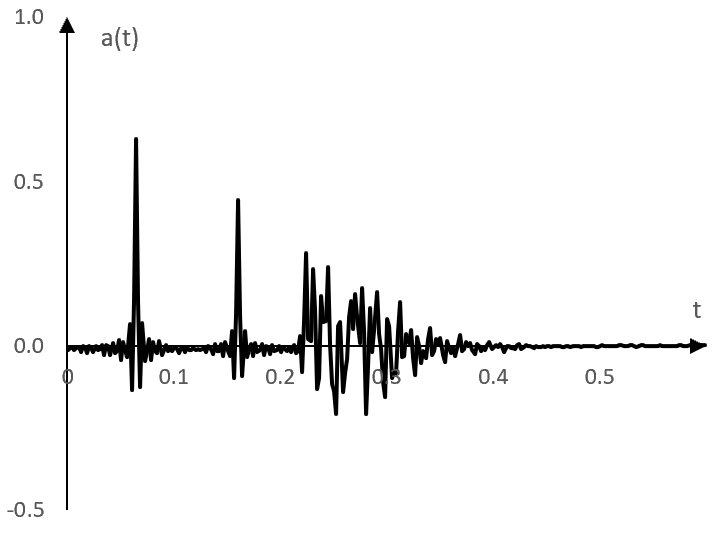
Note that the pre-ringing, if not adjusted for, may cause a notable decrease in the amplitude of high frequencies in the signal, to which the impulse response is applied later.

Deconvolution in the frequency domain

The deconvolution (the convolution with the time inverted sine sweep) in the example above was performed in the time domain. That is, each value a(k) of the impulse response at sample k was computed as the convolution of the time inverted sine sweep x(k) and the result of the first convolution h(k) as follows.

$$a(k)=\sum_{n=0}^{N} x(n) \, h(k-(N-n))$$

where N is the length of the sine sweep. Sine sweeps, however, and sine sweep recordings in practice could be relatively long, which would make this convolution very slow. An alternative is to use convolution or deconvolution in the frequency domain, relying on the fact that the Fourier transform of a convolution of two functions is the product of the Fourier transforms of the two functions.

$$F(h)=F(a * x)=F(a)\,F(x)$$

This, for example, the impulse response is the inverse Fourier transform of the division of the Fourier transform of the recorded sine sweep and the Fourier transform of the sine sweep.