Едно синусоидно помитане е една синусоида, която плавно променя честотата с времето.
Синусоидното помитане също се нарича и "честотно помитане" или "чуруликане" (от англ., "chirp").
Функциите
$$x(t)=\sin(2\,\pi(f_0\, t+\frac{f_1-f_0}{2\,T}t^2))$$
и
$$x(t)=\sin(2\,\pi\,f_0 \,T \frac{(\frac{f_1}{f_0})^{\frac{t}{T}}-1}{\ln(\frac{f_1}{f_0})})$$
например, променят честотата от f0 до f1 за времето T. Първата функция се нарича линейно синусоидно помитане, защото производната на честотната част вътре във синуса е линейна спрямо времето t. Подобно, втората функция се едно експоненциално синусоидно помитане.
И двете функции имат начална фаза равна на нула. Една различна начална фаза може да бъде добавена както при всяка друга синусоида, ако е необходима. И в двете функции, заместването на t с k / fs, където k = 0, 1, 2, … и fs е пробната честота, дава дискретизирания вариант на функцията.
Пример на едно синусоидно помитане
Следното е едно експоненциално синусоидно помитане, което променя честотата от 1 Hz до 50 Hz в 2 секунди.
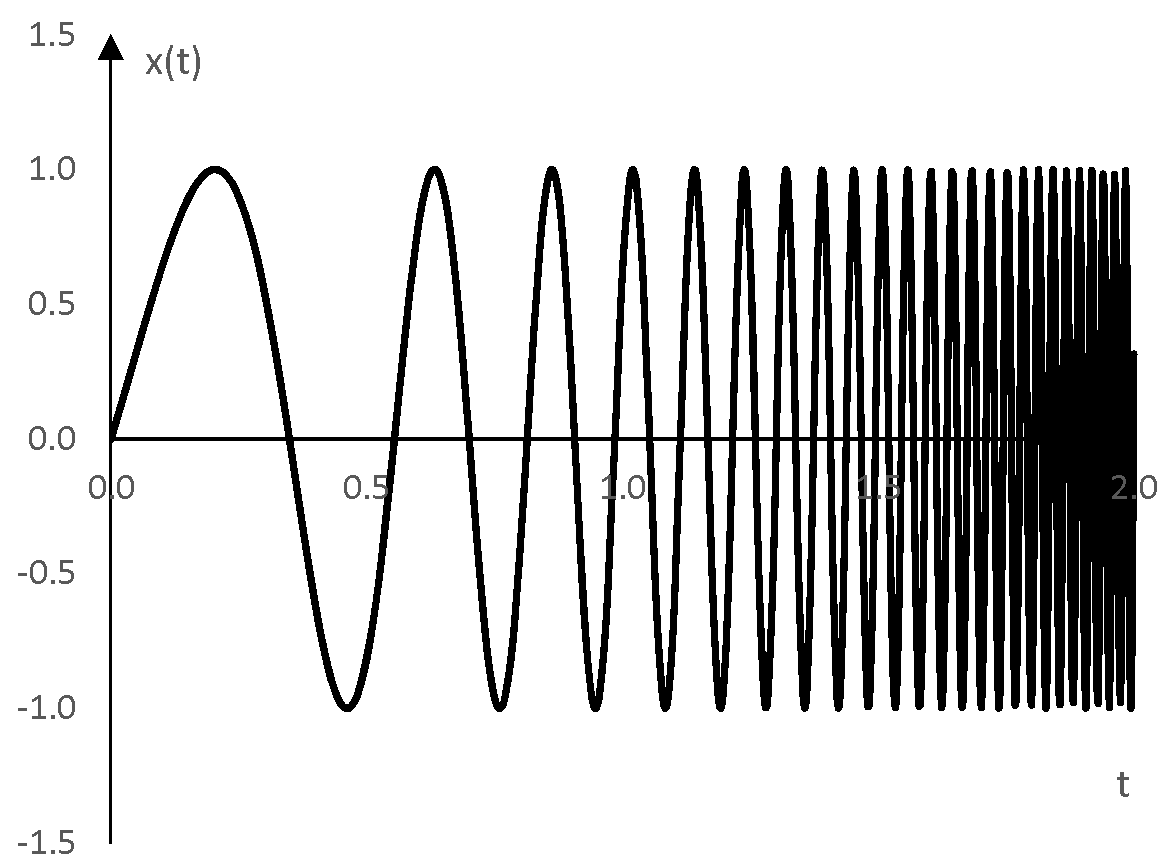
Звукът на синусоидното помитане
Следното е линейното синусоидно помитане, създадено с формулата по-горе, където началната честота f0 е 50 Hz, крайната честота f1 е 1000 Hz и времето T е 1 секунда.
Щракни на бутона за да чуеш линейното синусоидно помитане.
Следното е експоненциалното синусоидно помитане със същите параметри – помитане на честотите от 50 Hz до 1000 Hz в 1 секунда.
Щракни на бутона за да чуеш експоненциалното синусоидно помитане.
Използване на синусоидното помитане
Синусоидното помитане е полезно при разработването на импулсния спектър на естествените реверберации за да се създаде един импулсен ривърб. На практика, може да се изсвири синусоидното помитане в една стая, да се запише резултата и да се използва деконволюция на резултата със синусоидното помитане, обърнато във времето, за да се получи импулса на ривърба.
Един пример на това е по-долу. Обикновено, едно синусоидно помитане, което се използва за тази цел, минава през целия честотен диапазон (например между 20 Hz и 22 kHz за целия диапазон на човешкото чуване и за да покрие максимума, възможен при пробната честота 44.1 kHz). Препоръките, за колко дълго трябва да се синусоидното помитане, са различни, но обикновено са между 3 секунди и 20 секунди. За примера по-долу, за да е по лесно да го представим, използваме по-кратко синусоидно помитане, което не минава през целия честотен диапазон.
Вземи следния импулсен спектър a(t).
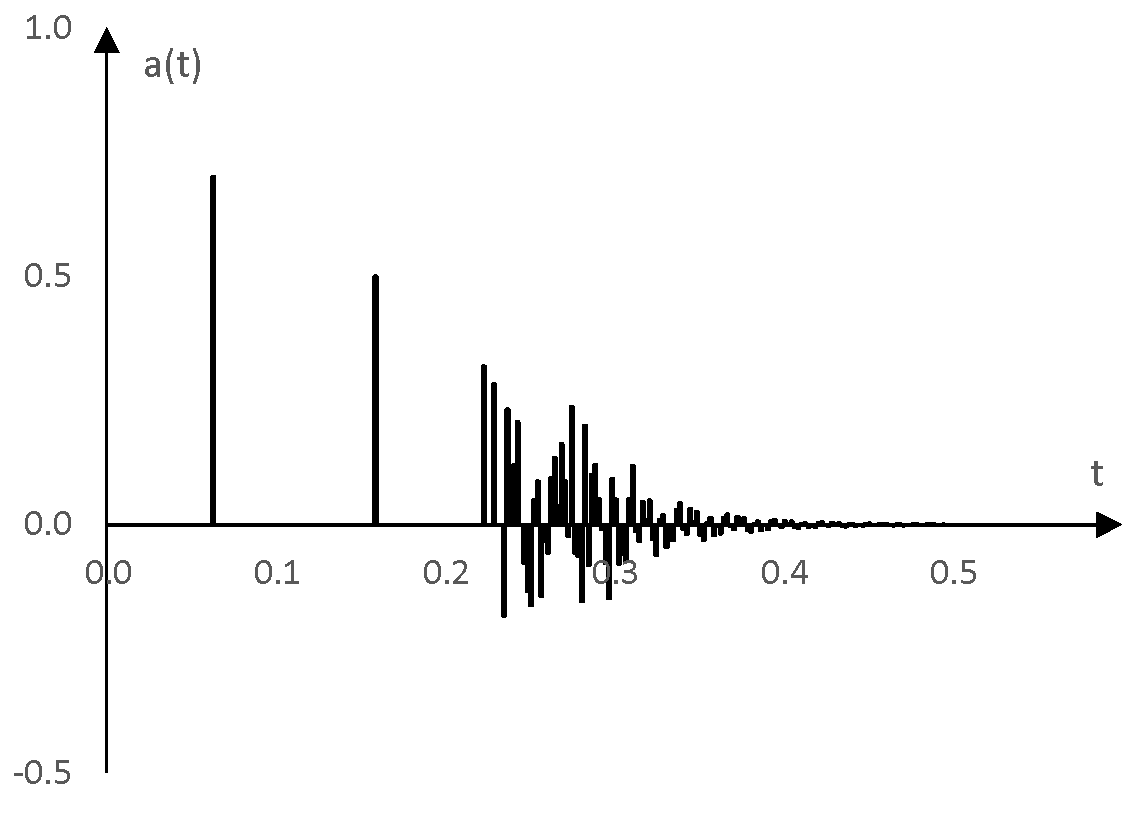
Тази графика имитира импулсния спектър на някакъв ривърб. Беше произведена, като се пусна един импулс през един напредващ гребенов филтър и като се пусна изхода на гребеновия филтър през един всичкопропускащ филтър на Шрьодер (виж Всичкопропускащ филтр). Това е един импулсен спектър от 300 точки при пробната честота 500 Hz.
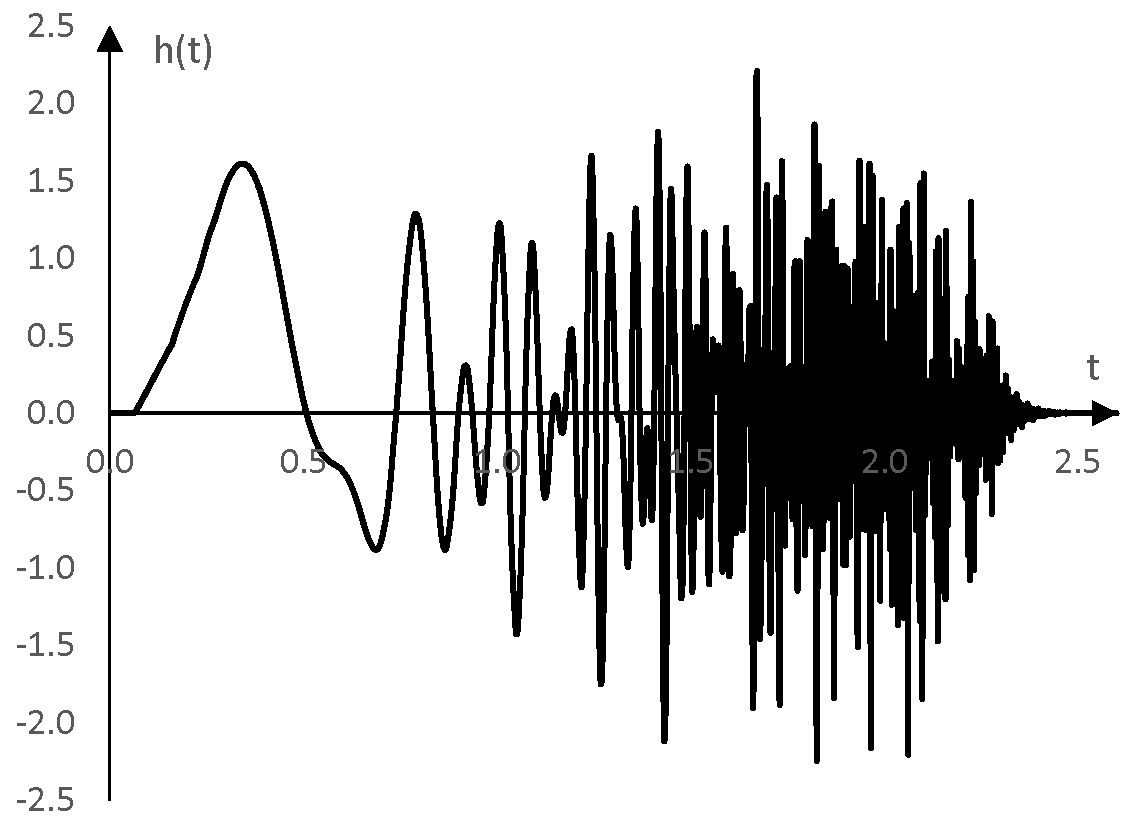
Изчисли конволюцията на този импулсен спектър с експоненциалното синусоидно помитане между 1 Hz и 200 Hz. Конволюцията h(t), която сама по себе си не е толкова интересна, е следната.
На практика, когато запишем естествените реверберации на едно синусоидно помитане, ще имаме този резултат и ще знаем какво синусоидно помитане е използвано, но няма да знаем импулсния спектър. За да получим импулсния спектър, можем да изчислим конволюцията на този резултат със същото синусоидно помитане, но обърнато във времето. Ако направим това в този пример, ще получим следния импулсен спектър.
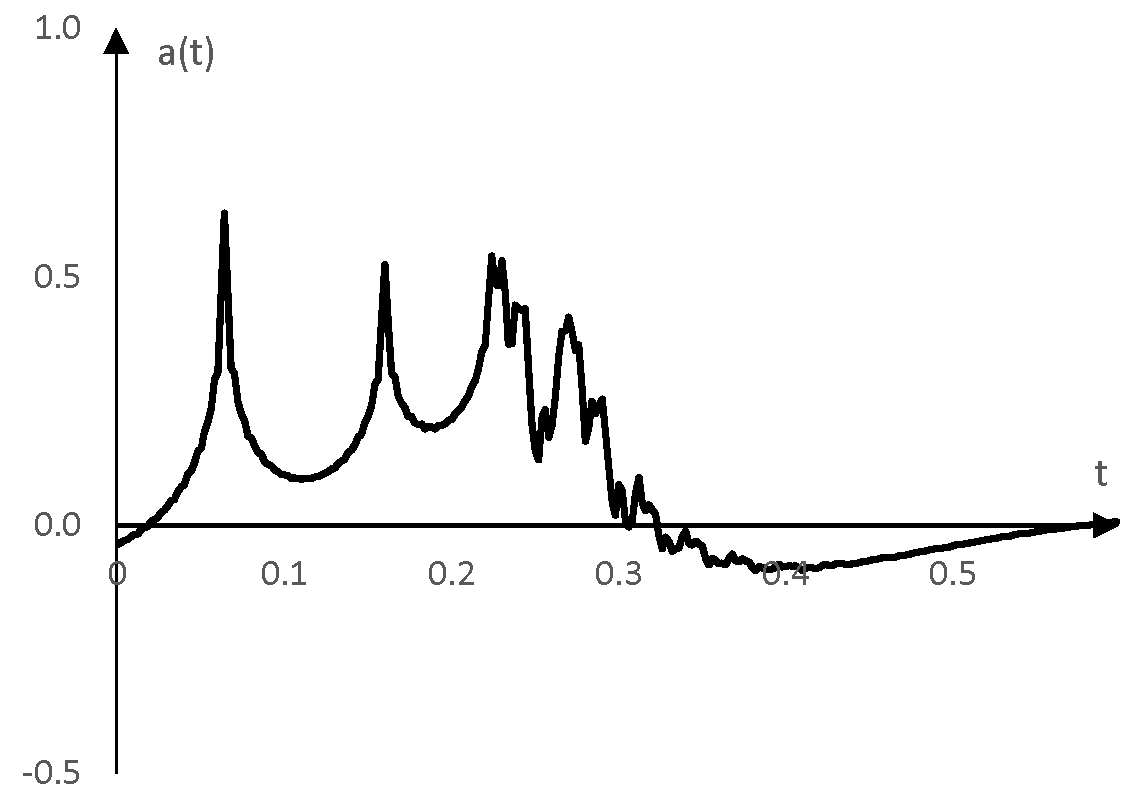
Този импулсен спектър е доста близък до началния импулсен спектър.
Има обаче доста "предно звънене". Изчисленият импулсен спектър не скача бързо от нула към първия връх, а прави това плавно.
Методът, който се използва за да се намали това предно звънене, е да се използва деконволюция с със синусоидното помитане, обърнато във времето, но и с променена амплитуда. Намаляваме амплитудата на честотите в синусоидното помитане с 6 dB на октава. Нагласяването на амплитудата ще бъде 0 dB (без промяна) в края с високите честоти и плавно ще се намали до
$$-6 \, \log_2 \frac{f_1}{f_0}$$
при ниските честоти. В примера тук, тъй като честотите на синусоидното помитане се променят от 1 Hz до 200 Hz, амплитудата над синусоидното помитане ще се промени плавно, линейно от 0 dB при 200 Hz до -46 dB при 1 Hz.
Новият импулсен спектър, след като променим амплитудата на синусоидното помитане, което се използва в деконволюцията (и след като добавим малко амплитуда към резултата), е следното.
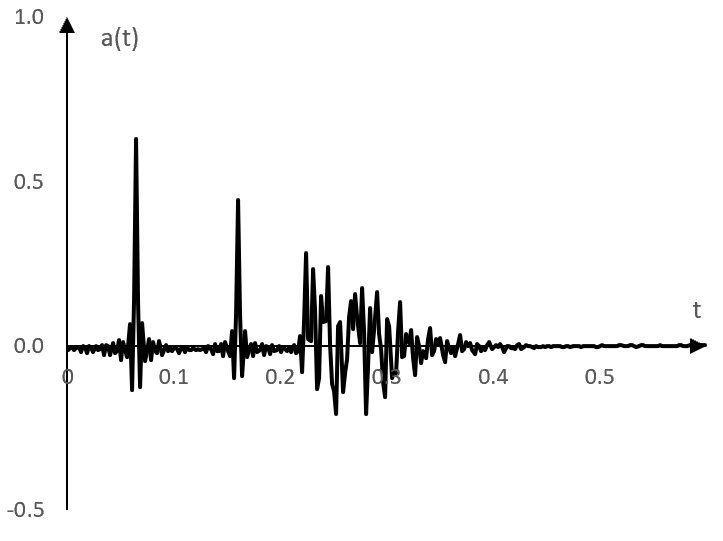
Забележи, че ако това предно звънене не се премахне, то може да причини намаляване на амплитудите на високите честоти в сигналите, върху които се използва този амплитуден спектър.
Деконволюция в честотния диапазон
Деконволюцията (конволюцията със синусоидното помитане, обърнато във времето) в горния пример бе извършено във диапазона на времето. Тоест, всяка стойност a(k) на импулсния спектър при проба k бе изчислена с конволюцията на синусоидното помитане x(k), обърнато във времето и резултатът от първата конволюция h(k) по следния начин.
$$a(k)=\sum_{n=0}^{N} x(n) \, h(k-(N-n))$$
където N е дължината на синусоидното помитане. Синусоидните помитания, обаче, а и записите на синусоидните помитания на практика може да са доста дълги, което ще направи тази конволюция доста бавна. Друга възможност е да се използва деконволюция в честотния диапазон, като разчитаме на факта, че преобразуването на Фурие на една конволюция на две функции е равна на умножението на преобразуванията на Фурие на двете функции.
$$F(h)=F(a * x)=F(a)\,F(x)$$
Така например, импулсният спектър е обратното преобразуване на Фурие на отношението на преобразуването на Фурие на записаното синусоидно помитане и преобразуването на Фурие на синусоидното помитане.

Добави нов коментар