An equiripple filter is simply a filter with ripples of equal height.
The magnitude response of actual digital filters may exhibit ripples. For example, the magnitude response of a finite impulse response low pass filter may have ripples close to its cutoff frequency, because the typical filter construction will use continuous functions (e.g., with the Fourier transform) to approximate a discontinuous ideal magnitude response. These ripples are the manifestation of the Gibbs phenomenon.
The fact that equiripple filters have ripples of equal height should not mean much. It is more important that the design of equiripple filters is such that the height of these ripples can be controlled. This itself is not unique of equiripple filters.
A digital IIR equiripple filter
The elliptic filter is an equiripple infinite impulse response filter.
A digital FIR equiripple filter
A finite impulse response equiripple filter can be designed with successive iterations between the forward and inverse discrete Fourier transform (DFT). The following is an example.
Suppose that we want to design a low pass FIR filter or length N = 39 at the cutoff frequency fc = 150 Hz, given the sampling frequency fs = 2000 Hz. We would also want a magnitude response of the filter that is within ±0.3 (approximately ±0.25 dB) in the pass band and that does not exceed 0.3 (-30 dB) in the stop band. We define the stop band as anything over 500 Hz and the pass band as anything between 0 and 90 Hz. Anything in between 90 Hz and 500 Hz would be the transition band of the filter.
We begin with the inverse discrete Fourier transform of the desired ideal magnitude response. We choose a transform of, say, 201 points and we create a desired ideal magnitude response that is symmetric around the origin.
$$|H(k)|=\begin{cases} 0, & k=-100,-99,...,-16 \\ 1, & k=-15,-14,...,15 \\ 0, & k=16, 17, ..., 100\end{cases}$$
Suppose that the sampling frequency is 2000 Hz. Then the 201 components of the inverse DFT would be evenly spaced at 2000 / 201 ≈ 9.95 Hz and component 15 is at -149.25 Hz. Thus, the magnitude response, as defined above, for this specific inverse DFT, can also be written as
$$|H(f)|=\begin{cases} 0, & f \lt -149.25\,Hz \\ 1, & -149.25\,Hz \le f \le 149.25\,Hz \\ 0, & f \gt 149.25\,Hz\end{cases}$$
This is an ideal magnitude response for a low pass filter at approximately 150 Hz. We compute the filter a(k) with the generalized inverse DFT as follows.
$$a(k+100)=\frac{1}{102} \sum_{n=-100}^{100} {|H(n)| \, \cos(\frac{2\pi k n}{201})}$$
k = -100, -99, …, 100. The inverse DFT would produce a filter of 201 points. Since we are only interested in a filter of 39 points, we take the middle 39 points from the initial 201.
$$a(k)=\begin{cases} 0, \,k \le 80 \\ a(k), \,80 \lt k \lt 120 \\ 0, \,k \ge 120 \end{cases}$$
We test the resulting filter with the forward DFT.
$$H(k)=\sum_{n=0}^{201} {a(k) (\cos(\frac{2\pi k n}{201})-j \,\sin(\frac{2\pi k n}{201}))}$$
k = -100, -99, …, 100. The magnitude response of this filter is
$$|H(k)|=\sqrt{Re(H(k))^2+Im(H(k))^2}$$
This magnitude response is shown below. The magnitude response does not satisfy all proposed criteria. Although the stop band is already under 0.3, the pass band is not within the proposed limits between 0.97 and 1.03 (see the dashed lines).
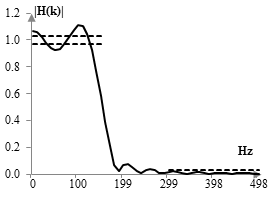
We correct the magnitude response, by forcing it within the proposed limits. In the pass band, for DFT components between -90 Hz and 90 Hz (i.e., k = -9, 8, …, 9).
$$|H(k)|=\begin{cases} 1.03, \, |H(k)| \gt 1.03 \\ 0.97, \, |H(k)| \lt 0.97 \\ |H(k)|, \, 0.97 \le |H(k)| \le 1.03 \end{cases}$$
k = -9, -8, …, 9. In the stop band
$$|H(k)|=\begin{cases} 0.3, \, |H(k)| \gt 0.3 \\ |H(k)|, \, |H(k)| \le 0.3 \end{cases}$$
k = -50, -49, …, -30, 30, 31, …, 50.
To be safe, by the Nyquist-Shannon sampling theorem and since the inverse DFT produces redundant information on real data, we will also zero out |H(k)| outside of (-1000 Hz, 1000 Hz). |H(k)| = 0 for k = -100, -99, …, -51, 51, 52, …, 100.
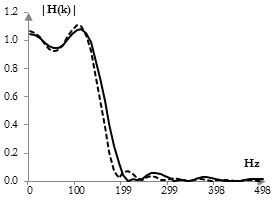
We take the inverse DFT on this new magnitude response and we repeat the DFT to test the resulting filter. We repeat this process several times. Each iteration will compress the larger ripples of the resulting filter – the ones exceeding the proposed criteria. After five iterations, for example, we obtain the magnitude response shown here (the dashed line shows the filter after one iteration; the solid line shows the filter after five iterations).
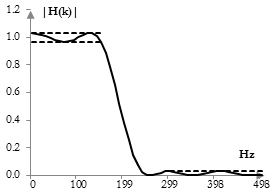
After a few more iterations, we obtain the filter shown below. This figure shows that this filter begins to converge to a filter with the proposed characteristics. Moreover, this filter has somewhat even ripples. The filter on this fugure uses 100 iterations, but that is a somewhat random choice.
The algorithm presented here does not always converge. The algorithm may not converge if, for example, the criteria are much stricter, such as if we wanted much smaller ripples or shorter transition band. The algorithm may also not converge, if the inverse and forward DFT operations are not precise enough, such as when the length of the DFT is shorter or even when the filter itself is shorter.
Using the inverse and forward DFT to produce an equiripple FIR filter is not the only available algorithm. The Parks-McCellan algorithm is another well-known iterative algorithm that uses Chebychev approximations instead of the forward DFT.
Add new comment