A saw wave is a periodic function that increases linearly from a minimum to a maximum and then drops suddenly back to the minimum. An inverted saw wave is similar, but decreases from a maximum to a minimum and then jumps back to the maximum.
In discrete time, for example, if N is the period of the function, then the function
$$x(k)=2\,(\frac{k}{N}+\mathrm{floor}(\frac{k}{N}+0.5))$$
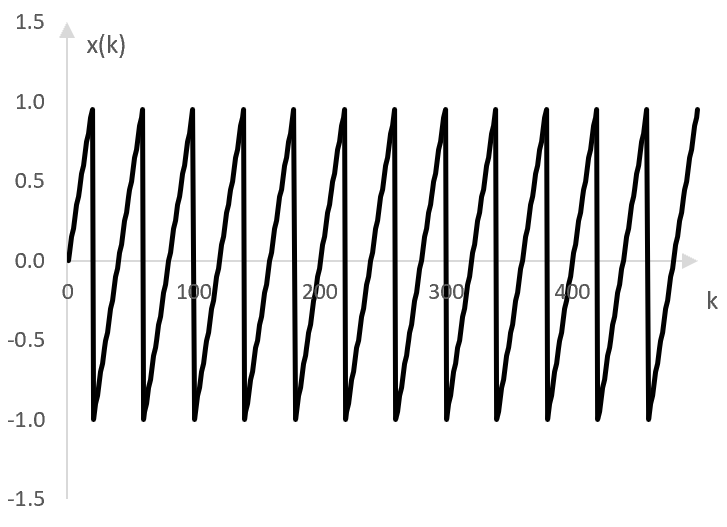
is a saw wave. It increases to 1 over N samples, then drops to -1, and again starts increasing back to 1. Its period is N samples. The "floor" function returns the closest integer that is smaller than its argument.
The function
$$x(k)=-2\,(\frac{k}{N}+\mathrm{floor}(\frac{k}{N}+0.5))$$
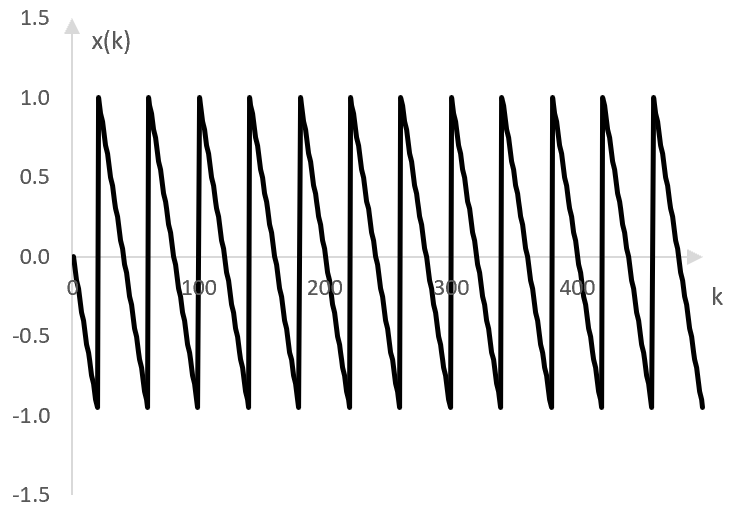
is an inverted saw wave.
If, for example, N = 40, then the saw wave will be as follows.
The inverted saw wave is shown below.
The following are two 5 second samples of a saw wave and an inverted saw wave, both with the frequency of middle C.
Click Play to hear a saw wave.
Click Play to hear an inverted saw wave.
Using saw waves
Much like square waves, saw waves are rich in harmonics. The following is the discrete Fourier transform of 500 components of the example saw wave in the graph above.
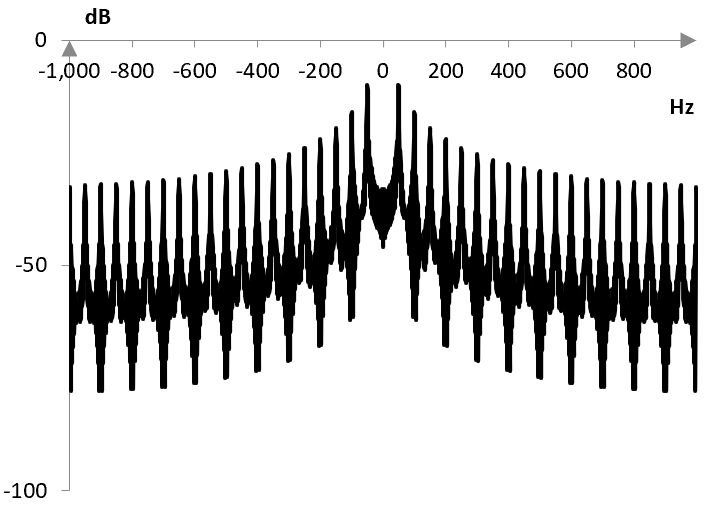
Because of these harmonics – the evenly spaced notches in the graph above – saw waves are used in synthesizers. To simulate the sound of an instrument, saw waves (as well as square waves and other) with the desired harmonics can be combined and the result filtered (e.g., through a low pass filter).
Harmonics of the saw wave
The peaks in the Fourier transform of a saw wave with frequency f occur at all integer harmonics of f. For example, since the frequency of the saw wave in the graph above is 50 Hz, the peaks occur at 50 Hz, 100 Hz, 150 Hz, 200 Hz, and so on.
In other words, the Fourier series expansion of the saw wave is an infinite sum of the harmonics of the saw wave frequency (as shown below, where each other one is with inverted phase).
Fourier series expansion of the saw wave
The Fourier series expansion at sample k of the saw wave is as follows.
$$\frac{2}{\pi} \sum_{n=1}^\infty \frac{(-1)^{n+1} \sin(\frac{2\,\pi\,k\,n\,f}{f_s})}{n}$$
where f is the frequency of the saw wave and fs is the sampling rate.
The Fourier series expansion of the inverted saw wave is
$$\frac{2}{\pi} \sum_{n=1}^\infty \frac{(-1)^{n} \sin(\frac{2\,\pi\,k\,n\,f}{f_s})}{n}$$
The following four graphs show the first term of the series sum, the sum of the first two terms, the sum of the first three terms, and the sum of the first eight terms for f = 33.3 Hz, fs = 16000 Hz and for the first 500 or so samples k on the horizontal axis.
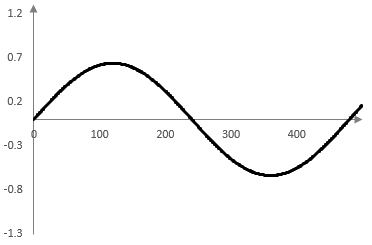
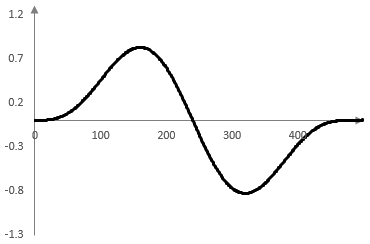
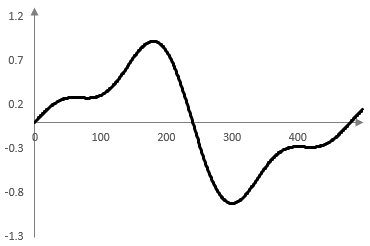
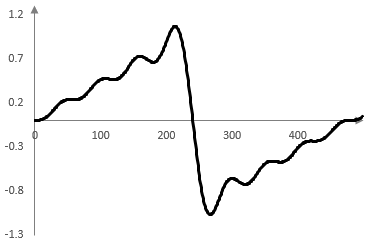
The ripples at the points where the saw wave is discontinuous the result of the Gibbs phenomenon – approximating a discontinuous function with a continuous function.

Add new comment