Транспониране - част 1

Ще разгледаме едно транспониране, защото е една от по-сложните преработки на цифровите сигнали за аудио. Ще използваме преобразуването на Фурие за да отчетем честотите. След това ще транспонираме тези честоти и ще изградим транспонирания сигнал.

Ще използваме следната подготовка:

• Пробна честота равна на 2000 Hz: Една ниска пробна честота прави графиките по-лесни.
• Дискретизирано преобразуване на Фурие (DFT) с дължина 32: Въпреки, че DFT-то може да използва каквато и да е дължина, един типична преработка на аудио ще използва алгоритъма за бързото преобразуване на Фурие и за този алгоритъм трябва дължина, която е някаква степен на 2.
• Застъпване на DFT равно на 75 процента: Не можем да изчислим DFT-то на целия сигнал и трябва да го направим на части (на кадри). За да получим един горе долу плавен резултат, тези части ще се застъпват. Ще напишем повече за това застъпване по-нататък.
• Входна честота равна на 70 Hz: Няма нищо специално тук, но е добре да отбележим две неща. Първо, работим с един сигнал с една честота. На практика, сигналите ще съдържат много честоти. Изчисленията обаче са същите. Второ, ако пробната честота е 2000 Hz и DFT-то използва 32 проби (или "кофи"), тогава кофите в DFT-то са на всеки 2000/32 = 62.5 Hz. Така, 70 Hz не е точно в една от тези кофи на DFT-то. Транспонирането на една честота, която не е точно в една от кофите на DFT-то ще ни покаже някои проблеми при DFT-то, които иначе няма да видим.
• Транспониране с 1.0594: Пак, няма нищо особено тук, освен това, че един полутон е 2^1/12 = 1.0594. Ще транспонираме 70 Hz с един полутон на около 74.2 Hz.
• Прозорци: Ще използваме прозореца на Хан и при разлагането на сигнала с DFT-то, и при изграждането на един нов сигнал с обратното DFT. Ще пишем повече за това по-нататък.

Входен сигнал

Входният цифров сигнал тук е просто

$$f(k) = cos(\frac{2 \pi k 70}{2000})$$

където k са пробите (k = 0, 1, 2, …), 70 е честотата на сигнала и 2000 е пробната честота.

Слагаме тази формула тук само ако някой иска да повтори това упражнение. Няма да изписваме формулите за изчисленията, които се знаят, като например DFT-то.

Ето първите 32 проби на сигнала.

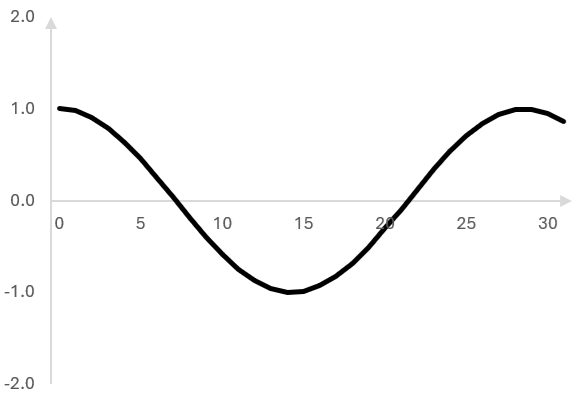
Сигналът може разбира се да продължи безкрайно.

Разлагане с DFT

Когато използваме DFT-то с дължина 32 върху тези 32 проби, можем да изчислим, че честотите на кофите на DFT-то имат следните амплитуди.

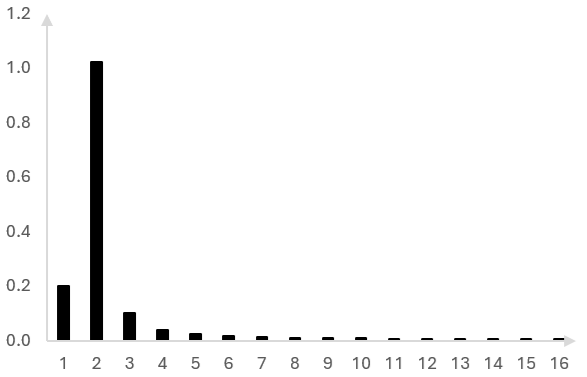
Хоризонталната ос показва първата половина от кофите в DFT-то. Показваме само половината от DFT-то, а не всичките 32 кофи. Втората половина на DFT-то върху един сигнал с реални стойности произвежда същите стойности и е излишна.

Тъй като 70 Hz не е точно в една от кофите на DFT-то, имаме спектрална оттичане. Имаме амплитуди във всяка от кофите, въпреки че използваме само една честота. Това няма да пречи на нашето транспониране, защото ще използваме всичката информация и ще работим с всички кофи.

Тази графика не ни изненадва. 70 Hz е близо до втората кофа на DFT-то, при 62.5 Hz и повечето от амплитудата се появява там.

DFT-то произвежда и фазите на честотите във всяка кофа. Тези фази са много важни и ще пишем за тях по-нататък.

Ще наречем първите 32 проби първия кадър. При записаното аудио, сигналът ще се променя с времето. Не можем просто да разчитаме на първите 32 проби. Ще трябва да изчислим DFT-то не само за първите 32 проби, но и за следващите и следващите и така нататък докато разберем съдържанието на целия сигнал във времето. Така, ще работим кадър по кадър.

Прозорец на Хан

Изчислихме DFT-то на сигнала такъв, какъвто беше, но е по-добре да приложим един прозорец преди това. Ще направим това и ще изчислим DFT-то наново.

Ще използваме прозореца на Хан с дължина 32 и ще умножим стойностите на сигнала на всяка проба със стойността на прозореца на тази проба.

Ето сигнала след прозореца (непрекъснатата линия) до оригиналния сигнал (прекъснатата линия).

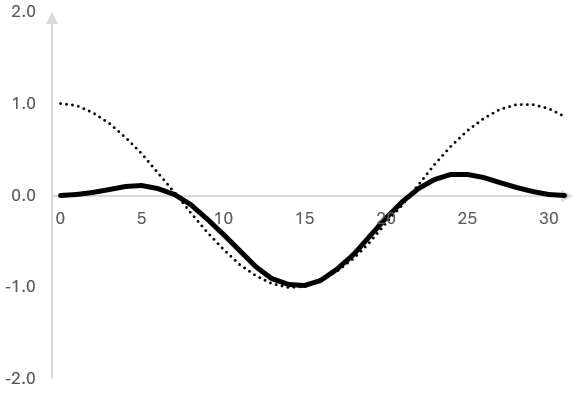
Прозорецът на Хан потиска лявата и дясната страна на кадъра на сигнала.

Ще изчислим DFT-то на този нов сигнал, но също така:

• Ще махнем първата кофа на DFT-то (нулевата честота), като направим нейната амплитуда нула. Прозорецът на Хан може да влоши тези стойности и да измести транспонирания сигнал.
• Ще умножим получените амплитуда по кохерентната амплитуда на прозореца на Хан. Когато потиска страните на сигнала, прозорецът на Хан намалява амплитудата на сигнала с тази кохерентна амплитуда. Кохерентната амплитуда е просто средното на стойностите на прозореца на Хан и, за прозореца на Хан, е приблизително 0.5 (т.е., делим по 0.5).

  Ето амплитудите на кофите на DFT-то както бяха изчислени по-горе, без прозореца (колоните на точки) и с прозореца (плътните колони).

  

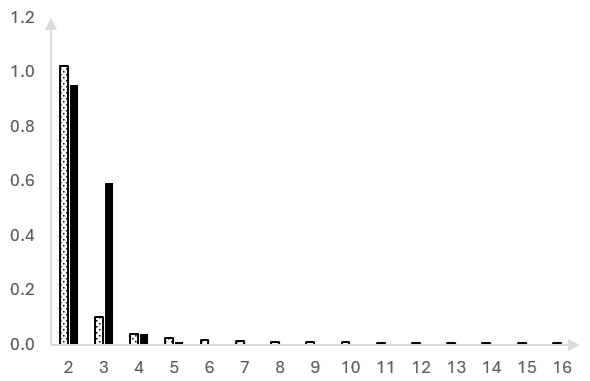
  Това може би изглежда по-лошо. Оригиналният връх на амплитудата сега се разпределя на две кофи.

  Но фокусирай се в кофите по-нататък.

  

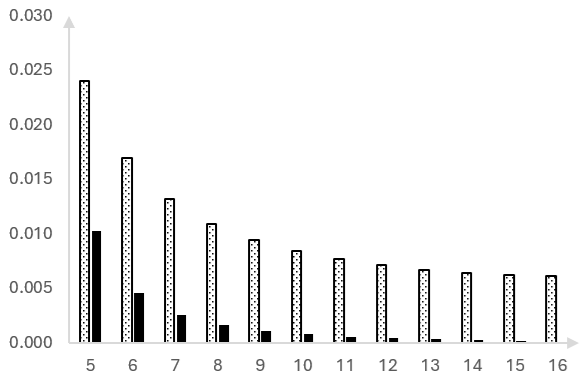
  Прозорецът наистина премести амплитудите, които преди "протичаха" в по-високите кофи, обратно към по-ниските кофи, близо до входната честота от 70 Hz.

  Следващи стъпки

  Това е първата стъпка: разлагаме оригиналния сигнал в един комплект амплитуди и фази. В следващата статия ще изчислим амплитудите и фазите на транспонирания сигнал. С последната стъпка ще изградим новия, транспониран сигнал.

  автори: mic