Един импулсен ривърб, също така наречен "ривърб с конволюция", е ефект, който създава изкуствени реверберации чрез конволюция на импулсния спектър на някакви естествени реверберации със записания звук.
Ако имаме някакво пространство (стая или зала) с хубави естествени реверберации, можем да запишем сухата (без реверберации) и реверберираната версия на един и същи звук. Можем да използваме тези два сигнала за да изчислим импулсния спектър на естествените реверберации както в примера по-долу. Можем след това да използваме конволюцията на импулсния спектър с какъвто и да е записан звук за да произведем един изкуствен ривърб, който имитира естествените реверберации. Фактът, че импулсния спектър се конволюира със сигнала за да даде изкуствения ривърб, дава името "ривърб с конволюция".
Създаване на импулсни ривърби със синусоидни помитания и деконволюция в честотния диапазон
Един пример на този процес е представен в темата Синусоидно помитане. Синусоидните помитания са добри кандидати за звука, който може да се изсвири и запише, защото изчислението на импулса на ривърба от получения сигнал е лесно – изчислява се конволюцията на получения сигнал със синусоидното помитане, обърнато във времето, обикновено с някакви нагласявания на неговата амплитуда. Тъй като конволюцията може да изисква доста изчислителна мощност, ако е изпълнена в диапазона на времето, може да се изпълни в честотния диапазон.
Един теоретичен пример на изчисляването на импулсния ривърб с един кратък звук
Примерът по-долу е друг пример. Вместо да използва едно синусоидно помитане, използва един кратък звук. Това не е методът, който се предпочита, но по-лесно се разбира.
Кратките звуци бяха кандидати преди за звуците, които могат да се свирят и записват, защото се предполагаше, че ще е лесно да се изчисли импулса на ривърба, ако оригиналния сигнал наподобява един импулс.
Да предположим, че имаме два записа на един и същи удар по един барабан – един сух, без реверберации и един с естествените реверберации на стаята. Следната графика е един пример на това, как записаният сух удар по барабана може да изглежда.
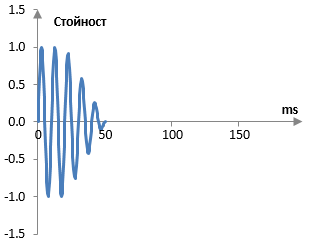
Реверберирания удар по барабана може да изглежда както в следната графика.
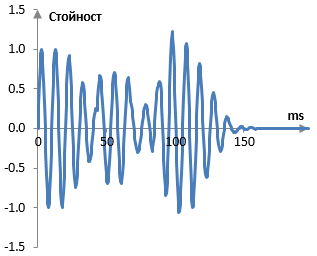
(Тези две графики не са действителни записи, а са просто примери, които вършат работа за целта на изчисленията по-долу. Ударът по барабане е просто една затихваща синусоида. Реверберираният удар използва един многоизходен дилей и един прост ривърб на Шрьодер. Многоизходният дилей има два изхода със забавяния равни на 43 милисекунди (ms) и 67 ms и затихвания равни на 0.7 и 0.5. Ривърбът на Шрьодер има два всичкопропускащи филтри на Шрьодер със забавяния 3.7 ms и 1.2 ms и затихвания 0.7 и 0.65 и един напредващ гребенов филтър със забавяне 11 ms и затихване 0.7.)
Ако имаме сухия и реверберирания сигнал, съответно x(k) и y(k), можем да изчислим импулсния спектър на ривърба, a(k). Тъй като и двата сигнала са ограничени (във времето), първата проба на конволюцията y(0) е изчислена само от една проба на импулсния спектър a(0) и една проба на удара по барабана x(0), втората проба на конволюцията е изчислена от две проби от импулсния спектър и удара по барабана и така нататък. Имаме следното
$$a(0) = \frac{y(0)}{x(0)}$$ $$a(1)=\frac{y(1)-a(0)x(0)}{x(1)}$$ $$a(2)=\frac{y(2)-a(0)x(0)-a(1)x(1)}{x(2)}$$ $$...$$
Импулсният спектър, получен с примера по-горе, е показан в следната графика.
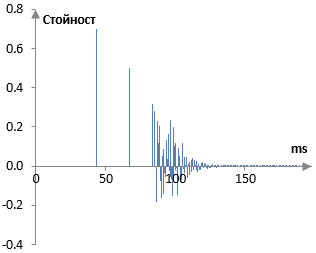
(В този определен случай, първите два върха на импулсния спектър са изходите на многоизходния дилей. Остатъкът е изхода от ривърба на Шръодер, в който всичкопропускащите филтри създават много на брой последователни повторения на сигнала и единствения връх в средата на тези много повторения е създаден от гребеновия филтър. Импулсният спектър по-горе не включва сухия сигнал и показва само реверберацията).
Изчисляване на импулсния спектър в практиката
На практика, изчисляването на импулсният спектър на естествените реверберации е по-трудно. Може би няма да можем прецизно да отделим сухия сигнал от реверберирания сигнал. Даже и ако можем да използваме два микрофона за да запишем сухия и реверберирания звук, най-вероятно: 1) част от реверберациите ще се появят в микрофона, който трябва да запише само сухия звук; 2) двата микрофона могат да запишат сухия сигнал по два различни начина.
Ако разликите са малки, изчисленията по-горе може все още да работят. Следната графика показва импулсния спектър изчислен по-горе (в синьо) и един импулсен спектър (в червено), изчислен със същия ревербериран записан сигнал, но с друг сух сигнал (един сух сигнал с малки случайни грешки между -0.02 и 0.02 във всяка от пробите).
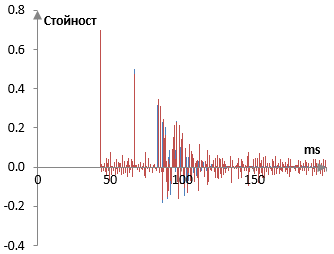
В някои случаи, както в случая тук, в зависимост от грешките, изчисленията по-горе могат да произведат един импулсен спектър, опашката на който не затихва или пък даже става безкрайно голяма. В тези случаи, импулсният спектър може изкуствено да се накара да затихне.
Също така, импулсният спектър може да се изчисли с оптимиране. Оптимирането ще търси импулсния спектър, който, при дадения записан сух удар по барабана, произвежда един ревербериран звук, който възможно най-добре наподобява записания ревербериран звук. Възможно е да създаде оптимиране, което подсигурява един затихващ импулсен спектър. Можем, например, да използваме оптимиране, в което структурата на ривърба е определена (например с един многоизходен дилей и един ривърб на Шрьодер) и което позволява промени само в параметрите на тази структура, но не и в самата структура.
Прилагането на импулсния спектър (конволюцията)
За да реверберираме който и да е звук, ще използваме конволюцията между импулсния спектър и този звук както в следната графика.
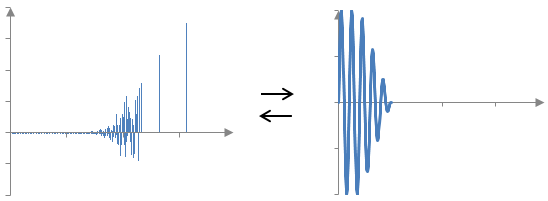
Ако a(k) е импулсният спектър с дължина N + 1 и x(k) е сухия сигнал, конволюцията изчислява реверберирания сигнал y(k) с формулата
$$y(k)=(a*x)(k)=\sum_{n=0}^{N} a(n)\,x(k-n)$$
Добави нов коментар