Гребенов филтър

Общата форма на един "напредващ" гребенов филтър е

$$y(k) = x(k) + w x(k – M)$$

като y(k) е изходния сигнал при пробата k, x(k) е входния сигнал при k, w е някакво число и M е положително цяло число.

Общата форма на един цифров гребенов филтър с обратна връзка е

$$y(k) = x(k) + w y(k – M)$$

"Напредващи" гребенови филтри

Да предположим, че един напредващ гребенов филтър е определен от формулата

$$y(k) = x(k) + 0.8 x(k – 50)$$

Този филтър изчислява изходния сигнал като сума на входния сигнал в същата проба и входния сигнал преди 50 проби с амплитуда, която е 0.8 от оригиналната амплитуда. Този филтър е просто един дилей. Изходния сигнал е същият като входния, плюс едно повторение на входния сигнал със забавяне във времето и затихване в амплитудата. В този пример забавянето е 50 проби, което, ако пробната честота е fs Hz, ще бъде 50 / fs секунди и затихването (загубата в амплитудата) е 20%.

Напредващите гребенови филтри са прости дилеи, които произвеждат сумата на входния сигнал с едно забавено и затихнало повторение на входния сигнал.

Трансферната функция на напредващите гребенови филтри, изчислена с преобразуването Z, е следната.

$$H(z) = 1 + w z^{-M}$$

Импулсният спектър на примерния филтър по-горе е ясен и е показан в следната графика.

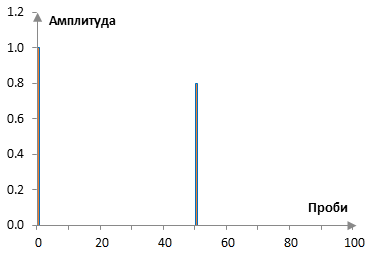
Амплитудният спектър на напредващия гребенов филтър се дава от формулата

$$|H(e^{j\omega})|=\sqrt{(1+w^2)+2w\,\cos(\omega M)}$$

където ω е ъгловата честота в радиани в секунда. Амплитудният спектър на примерния филтър по-горе, ако пробната честота е 2000 Hz, е показан в следната графика.

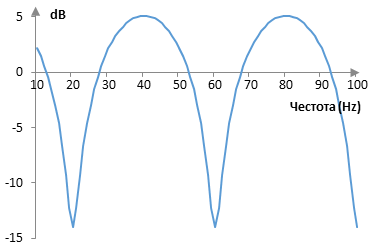
Този амплитуден спектър дава името на филтъра – "гребенов филтър".

Гребенови филтри с обратна връзка

Да предположим, че един гребенов филтър с обратна връзка е определен от формулата

$$y(k) = x(k) + 0.8 y(k – 50)$$

Този филтър изчислява изходния сигнал като сума от входния сигнал при същата проба и изходния сигнал преди 50 проби с амплитуда, която е 0.8 от оригиналната амплитуда. Можем да изпишем уравнението по-горе като

$$y(k) = x(k) + 0.8 y(k – 50)$$ $$= x(k) + 0.8 x(k – 50) + 0.8*0.8 y(k – 100)$$ $$= x(k) + 0.8 x(k – 50) + 0.8*0.8 x(k – 100) + 0.8*0.8*0.8 y(k – 150)$$ $$= …$$

Този филтър произвежда сумата на входния сигнал и няколко повторения на входния сигнал, които са все по-затихващи и все по-забавени. Този филтър е едно просто ехо. Ехото в примера по-горе е със забавяне от 50 проби (или 50 / fs секунди, ако пробната честота е fs проби в секунда) и със затихване (загуба в амплитудата) от 20%.

Гребеновият филтър с обратна връзка са просто ехо, което произвежда сумата на входния сигнал и няколко повторения на входния сигнал с непрекъснато по-малка амплитуда и с непрекъснато по-голямо забавяне. Затихването и забавянето между всеки две съседни повторения е едно и също.

Тъй като изходния сигнал влиза обратно във входа на филтъра, както в общата форма по-горе, се казва, че този филтър е с "обратна връзка". По същата причина този филтър е и филтър с неограничен импулсен спектър (IIR). На теория, импулсният спектър на този филтър може да продължи безкрайно.

Трансферната функция на гребеновия филтър с обратна връзка е следната.

$$H(z)=\frac{1}{1-w z^{-M}}$$

Следното е част от импулсния спектър на примерния филтър по-горе. Забележи, че импулсният спектър на този филтър е неограничен и че това е само частта върху първите 500 семпли.

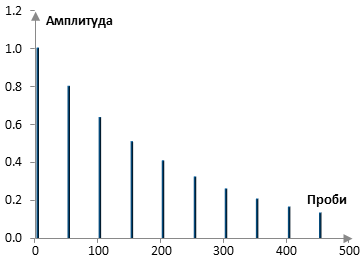
Амплитудният спектър на гребеновия филтър с обратна връзка може да се изчисли от неговата трансферна функция.

$$|H(e^{j \omega})|=\frac{1}{\sqrt{(1+w^2)-2w \, \cos(\omega M)}}$$

където ω е ъгловата честота в радиани в секунда. Амплитудният спектър на примерния филтър, ако пробната честота е 2000 Hz, е следния.

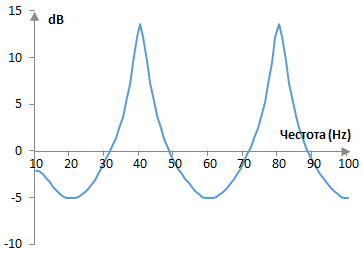
Периодичност на амплитудния спектър

"Зъбите" на двата филтъра се повтарят след всеки 40 Hz. Това може да се очаква, понеже ако пробната честота е 2000 Hz, тогава и двата филтъра забавят сигнала с 40 Hz = 2000 Hz / 50 проби. Зъбите стават по-чести, ако забавянето е по-голямо и по-редки, ако забавянето е по-малко.

Периодичността на амплитудния спектър на двата типа филтри може да се види и във формулите за амплитудния спектър, които са изчислени от трансферните функции. Периодичността идва от cos(ω M). В ъглови честоти, можем да очакваме, че периодите са 2 π / M.

Използване на гребеновите филтри

Напредващите гребенови филтри произвеждат прости дилеи. Няколко такива филтри могат да произведат, да кажем, един многоизходен дилей. Гребеновите филтри с обратна връзка произвеждат ехо. Няколко такива филтри могат да произведат един многоизходен дилей с обратна връзка. Гребеновите филтри са много полезни и при проектирането на изкуствени ривърби, защото реверберациите са просто една сбирка от различни форми на ехото (виж Ривърб на Шрьодер).