Един всичкопропускащ филтър е честотен филтър, който пропуска всички честоти и запазва амплитудата на всички честоти в сигнала.
Както е описано по-долу, въпреки че всичкопропускащите филтри нямат интересни амплитудни спектри (начинът, по който те променят амплитудата на честотите в сигнала, не е интересен), те могат да имат други полезни характеристики.
Най-простият всичкопропускащ филтър
Един типичен филтър a(n) с ограничен импулсен спектър и с дължина N, входния сигнал на който е x(k), изчислява изходния сигнал y(k) с формулата
$$y(k) = \sum_{n=0}^{N-1} a(n) x(k-n)$$
Така, изходният сигнал y(k) при пробата k е равен на сумата от сегашната и предишните N – 1 стойности на входния сигнал x(k), където N-те тежести на сумата са стойностите на филтъра a(n), n = 0, 1, …, N – 1.
Най-простият всичкопропускащ филтър тогава е филтъра с дължина N = 1, който се дава от формулата
$$a(0)=1$$
Този филтър дава просто
$$y(k)=x(k)$$
и не променя входния сигнал. Ясно е, че това е един всичкопропускащ филтър, защото всички честоти, които се съдържат в сигнала x(k), ще останат с непроменена амплитуда в y(k). Разбира се, този филтър няма много практически приложения.
Всичкопропускащ филтър с ограничен импулсен спектър
Един полезен всичкопропускащ филтър с ограничен импулсен спектър (FIR) и с нечетна дължина N е
$$a(n)=\begin{cases} 1, & n=\frac{N-1}{2} \\ 0, & n \ne\frac{N-1}{2}\end{cases}$$
Ако изчислим изходния сигнал със сумата по-горе и с този филтър, ще получим
$$y(k)=x(k-\frac{N-1}{2})$$
където y(k) е изходния сигнал при проба k, x(k) е входния сигнал при проба k и N е дължината на филтъра.
Трансферната функция на този филтър с преобразуването Z е
$$H(z)=z^{-\frac{N-1}{2}}$$
Това е един всичкопропускащ филтър, защото всяка честота във входния сигнал x(k) ще остане в изходния сигнал на филтъра y(k) с непроменена амплитуда. С други думи, амплитудният спектър на този филтър, изчислен на кръга с радиус 1 при z = ej ω, е
$$|H(e^{j \omega})|=|e^{-j \omega \frac{N-1}{2}}|=1$$
Амплитудният спектър е равен на 1 за всички честоти. Това наистина е един всичкопропускащ филтър.
Приложение на всичкопропускащия филтър с ограничен импулсен спектър
Въпреки че всичкопропускащият филтър по-горе не променя амплитудите на честотите, той забавя всяка честота във входния сигнал x(k) с (N – 1) / 2 проби. Можем да кажем, че този филтър има забавяне във фазата равно на (N – 1) / 2 проби за всяка честота или пък на (N – 1) / (2 fs) секунди, ако пробната честота (честотата на дискретизирането) е fs проби в секунда.
Вземи един нискочестотен филтър с ограничен импулсен спектър и със същата дължина N. Можем да покажем, че, ако коефициентите на този филтър са симетрични спрямо средата (N – 1) / 2, филтърът ще произведе същото забавяне във фазата от (N – 1) / 2 проби за всички честоти (виж фазов спектър). Това означава, че изходните сигнали от нискочестотния филтър и от всичкопропускащия филтър могат да се комбинират без проблеми. Изходният сигнал от нискочестотния филтър може да бъде изваден от изходния сигнал на всичкопропускащия филтър за да се получи един високочестотен филтър. Всичкопропускащият филтър пропуска всички честоти, нискочестотният филтър пропуска само ниските честоти и разликата между двата сигнала ще съдържа само високите честоти.
Също така, ако aL(n) е нискочестотния филтър и aA(n) е всичкопропускащия филтър, тогава изходният сигнал е
$$y(k)=\sum_{n=0}^{N-1}a_A(n)x(k-n)-\sum_{n=0}^{N-1}a_L(n)x(k-n)=\sum_{n=0}^{N-1}(a_A(n)-a_L(n))x(k-n)$$
Това означава, че, вместо първо да изчислим изходните сигнали от двата филтъра и после да ги извадим, можем да просто да създадем един високочестотен филтър с коефициенти aA(n) –aL(n). Например, ако използваме стандартния нискочестотен филтър
$$a_L(n)=\begin{cases} \frac {sin(\frac{2\pi f_c(n-\frac{N-1}{2})}{f_s})}{\pi (n-\frac{N-1}{2})}, & n\ne\frac{N-1}{2} \\ 2\frac{f_c}{f_s}, & n=\frac{N-1}{2}\end{cases}$$
можем да вземем всичкопропускащия филтър по горе и да произведем високочестотния филтър
$$a_H(n)=\begin{cases} \frac {sin(\frac{2\pi f_c(n-\frac{N-1}{2})}{f_s})}{\pi (n-\frac{N-1}{2})}, & n\ne\frac{N-1}{2} \\ 1-2\frac{f_c}{f_s}, & n=\frac{N-1}{2}\end{cases}$$
Всичкопропускащите филтри с ограничени импулси спектри се използват за да произведат преобразувания на филтрите – за да преобразуват един нискочестотен филтър във високочестотен филтър. Това преобразуване на филтъра се нарича "(спектрално) обръщане на филтъра".
Всичкопропускащи филтри с неограничен импулсен спектър
Всички всичкопропускащи филтри с неограничени (безкрайни) импулсни спектри и с реални коефициенти имат следната трансферна функция.
$$H(z)=z^{-M} \frac{a_N+a_{N-1}z^{-1}+a_{N-2}z^{-2}+...+z^{-N}}{1+a_1z^{-1}+a_2z^{-2}+...+a_Nz^{-N}}$$
където M и N са някакви неотрицателни цели числа. Амплитудният спектър на този филтър върху кръга с радиус 1 при z = ej ω е следния.
$$|H(e^{j\omega})|=|z^{-M} \frac{a_N+a_{N-1}z^{-1}+a_{N-2}z^{-2}+...+z^{-N}}{1+a_1z^{-1}+a_2z^{-2}+...+a_Nz^{-N}}|$$ $$=|\frac{z^{-M}}{z^{-N}} \frac{a_Nz^{-N}+a_{N-1}z^{-(N-1)}+a_{N-2}z^{-(N-2)}+...+1}{1+a_1z^{-1}+a_2z^{-2}+...+a_Nz^{-N}}|=|e^{j\omega(N-M)}|=1$$
Така, това е един всичкопропускащ филтър.
Приложения на всичкопропускащия филтър с неограничен импулсен спектър и всичкопропускащия филтър на Шрьодер
Можем да опитаме същото преобразуване, което използвахме при филтъра с ограничен импулсен спектър, за да създадем и високочестотен филтър с неограничен импулсен спектър. Ще трябва да изберем някакъв лесен и подходящ всичкопропускащ филтър, което може да е трудно, като се има предвид, че филтрите с неограничен импулсен спектър не се държат много добре в лентата на спиране. Амплитудният спектър на получения филтър, обаче, няма да е толкова добра, колкото може би се надявахме. Има по-добри методи за създаването на високочестотни филтри с неограничени импулсни спектри.
Един пример за по-полезен всичкопропускащ филтър с неограничен импулсен спектър е всичкопропускащия филтър на Шрьодер. Всичкопропускащият филтър на Шрьодер има трансферната функция
$$H(z)=\frac{g+z^{-N}}{1+gz^{-N}}$$
и изчислява изходния сигнал y(k) от входния сигнал x(k) с уравнението
$$y(k)=g \, x(k)+x(k-N)-g\,y(k-N)$$
където g е някаква амплитуда и N е някакво забавяне измерено в брой проби. Амплитудният спектър на този всичкопропускащ филтър е същия, както по-горе. Импулсният му спектър, обаче, е доста по-интересен. Следната графика показва импулсния спектър на всичкопропускащия филтър на Шрьодер с g = 0.7 и N = 20 проби и с пробната честота 2000 Hz (20 проби при 2000 Hz е равно на 10 милисекунди).
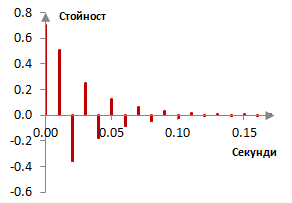
Всичкопропускащия филтър на Шрьодер създава много повторения на сигнала със непрекъснато затихваща амплитуда. Този всичкопропускащ филтър тогава може да се използва за да имитира многото повторения, които са създадени от естествената реверберация (виж Ривърб). Обикновено, няколко последователни всичкопропускащи филтри на Шрьодер се слагат преди няколко паралелни напредващи гребенови филтри за да произведат късната реверберация на Шрьодер. Или пък няколко паралелни нискочестотни гребенови филтри с обратна връзка на Шрьодер и Муурър се слагат преди няколко последователни всичкопропускащи филтри на Шрьодер. Повторенията от всичкопропускащия филтър на Шрьодер са много близко едно до друго и са много на брой, което имитира дифузията в естествената реверберация. В този случай, g обикновено е около 0.7 и N е такова, че дава забавяне от 100 / 3k милисекунди, k = 1, 2, …. Така, N дава забавяне от приблизително 33 ms, 11 ms, 3 ms и така нататък. Внимава се да се избере N, които са взаимно прости в различните всичкопропускащи филтри така, че повторенията на тези филтри да не съвпадат често.
Един специален случай на всичкопропускащия филтър на Шрьодер, с N = 1, може да се използва при фейзърите.
Общи форми на всичкопропускащите филтри
В по-общите си варианти, с комплексни числа, всичкопропускащите филтри с ограничени импулсни спектри имат трансферната функция
$$H(z)=e^{j\phi}z^{-M}$$
а всичкопропускащите филтри с неограничени импулсни спектри имат трансферната функция
$$H(z)=e^{j\phi}z^{-M}\frac{b_N+b_{N-1}z^{-1}+b_{N-2}z^{-2}+...+z^{-N}}{1+a_1z^{-1}+a_2z^{-2}+...+a_Nz^{-N}}$$
където ϕ е константна фаза, M и N са неотрицателни цели числа, b1 е комплексно спрегнатото число на a1, b2 е комплексно спрегнатото на a2 и така нататък. В сферата на реалните числа ϕ = 0 или ϕ = π.
Добави нов коментар