Нискочестотен филтър

Един нискочестотен филтър е честотен филтър, който позволява (пропуска) честотите под някаква преходна честота и не позволява (спира) честотите над тази преходна честота.

Пример на един нискочестотен филтър със звуково парче

Виж Orinj Нискочестотен филтър за да чуеш едно звуково парче преди и след един нискочестотен филтър.

Идеален нискочестотен филтър

Един идеален нискочестотен филтър е този, който пропуска всички ниски честоти – под преходната честота – с непроменена амплитуда и който напълно спира всички високи честоти. Амплитудата на ниските честоти в изходния сигнал ще бъде 100% от амплитудата на същите честоти във входния сигнал. Амплитудата на високите честоти в изходния сигнал ще бъде нула, независимо от това, какви са амплитудите на тези честоти във входния сигнал.

Следната графика показва амплитудния спектър на един идеален нискочестотен филтър с някаква преходна честота.

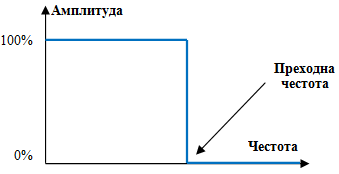
Всички честоти под преходната честота остават с тяхната входна амплитуда. Всички честоти над преходната честота са напълно премахнати.

Пример на един цифров нискочестотен филтър с ограничен импулсен спектър (FIR)

Един типичен филтър a(k) с ограничен импулсен спектър изчислява изходния сигнал y(n) от входния сигнал x(n) със следното средно аритметично.

$$y(n)=\sum_{k=0}^N a(k)\,x(n-k)$$

Един добър нискочестотен филтър a(k) е

$$a(k)=\begin{cases} \frac{\sin(\frac{2\pi f_c (k-\frac{N-1}{2})}{f_s})}{\pi(k-\frac{N-1}{2})}, k \ne \frac{N-1}{2} \\ 2 \frac{f_c}{f_s}, k=\frac{N-1}{2} \end{cases}$$

където f_s е пробната честота, N е дължината на филтъра (броя на термините в средното аритметично), а f_c е преходната честота.

Ако например f_s = 2000 Hz, f_c = 40 Hz и N = 201, амплитудният спектър на този филтър ще бъде както в следната графика.

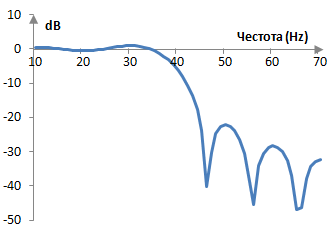
Амплитудният спектър на този филтър не е идеален. Така или иначе, филтърът оставя амплитудите на честотите под 40 Hz почти непроменени и понижава амплитудите на честотите над 40 Hz. Следователно, това е един нискочестотен филтър с преходната честота 40 Hz.

Пример на един цифров нискочестотен филтър с неограничен импулсен спектър (IIR)

Следното изчисление на изходния сигнал y(n) от входния сигнал x(n) е пример на един импулсно инвариантен нискочестотен филтър на Батъруърт от втори разряд

$$y(n)=0.22853 \, x(n-1)+1.19249 \, y(n-1)-0.42804 \, y(n-2)$$

с нормализирана преходна честота ω_c = 0.6 (действителна преходна честота ω_c * f_s / (2π)). Този филтър има трансферната функция

$$H(z)=\frac{0.22853 \, z^{-1}}{1-1.19249 \, z^{-1}-0.42804 \, z^{-2}}$$

Ако вземем например пробната честота f_s = 2000 Hz, преходната честота на този филтър става 0.6 * 2000 / (2π) = 191 Hz и съответният амплитуден спектър става следния.

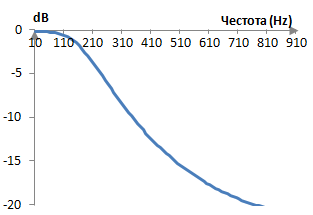
Този филтър запазва донякъде амплитудите на честотите под 191 Hz и намалява амплитудите на честотите над 191 Hz. Въпреки че този филтър не е идеален, това е един практичен нискочестотен филтър с преходна честота 191 Hz.

Извеждане на нискочестотния филтър с ограничен импулсен спектър

Търсеният амплитуден спектър на идеалния нискочестотен филтър може да се запише по следния начин.

$$|H(f)|=\begin{cases} 1, -\frac{f_c}{f_s} \le f \le \frac{f_c}{f_s} \\ 0, |f| \gt \frac{f_c}{f_s} \end{cases}$$

Това е идеалния амплитуден спектър на един нискочестотен филтър с нормализирана преходна честота f_c / f_s. Според теоремата за дискретизацията f_c / f_s < 1/2. Това, че се използва амплитуден спектър, който е симетричен около нулата, е полезно, понеже позволява на обратното преобразуване на Фурие да произведе един филтър с реални, а не с комплексни коефициенти.

Отбелязваме F = f_c / f_s. Обратното преобразуване на Фурие върху идеалния амплитуден спектър е

$$a(t)=\int_{-F}^F e^{2\pi j f t} df=\frac{1}{2\pi j t}(e^{2\pi j F t}-e^{-2\pi j F t})=\frac{1}{\pi t} \sin(2\pi F t)$$

Функцията sin(t) / t е функцията sinc(t) и затова филтрите с ограничени импулсни спектри понякога се наричат sinc функции. Тази функция в уравнението по-горе има увеличаващи се осцилации (колебания) до t = 0, където тя е a(0) = 2 F и след което има намаляващи осцилации. За да създадем един дискретен филтър, дискретизираме тази функция между -1 и 1 с дадената пробна честота.

$$a(k)=\frac{\sin(\frac{2\pi f_c k}{f_s})}{\pi k}, k=-(f_s-1), …, f_s -1$$

Избираме един дискретен филтър с дължина N от средните N точки на дискретизираната функция a(k) и изместваме филтъра надясно с (N – 1) / 2. Това дава формулата за нискочестотния филтър с ограничен импулсен спектър, показана по-горе. В средата на филтъра, при k = (N – 1) / 2, използваме правилото на Лопитал, което казва, че, ако границите на знаменателя и числителя са нула и границите на производните съществуват, тогава границата на отношението е равна на отношението на границите на производните.

Друго извеждане

Използваме факта, че пускането на един сигнал през един филтър с ограничен импулсен спектър е просто конволюцията на филтъра със сигнала. Конволюцията на един синус и един косинус с честоти равни на цели числа n₁ и n₂ е нула, ако двете цели числа са различни и е нещо различно от нула, ако n₁ = n₂.

$$\sum_{m=0}^{f_s-1}\cos(\frac{2\pi n_1 m}{f_s}) \, \sin(\frac{2\pi n_2(k-m)}{f_s}) \approx \begin{cases} 0, n_1 \ne n_2 \\ \frac{f_s}{2} \sin(\frac{2\pi n_1 k}{f_s}), n_1 = n_2 \end{cases} $$

където една от тези две прости вълни в конволюцията е ограничена в един интервал от единица време и е нула извън този интервал. Резултатите от конволюцията на два косинуса и на два синуса са подобни. С други думи, конволюцията на един сигнал с една правилно ограничена проста вълна на косинус или синус връща същата тази вълна, ако тя съществува в сигнала или пък връща нула, ако вълната не съществува в сигнала. Това означава, че можем да създадем един филтър, като сумираме всички прости вълни, които искаме този филтър да пропуска.

$$a(k)=\sum_{m} \cos(\frac{2\pi m k}{f_s}), m \lt f_c, k=1, …, f_s-1$$

Тъй като събираме честоти равни на цели числа, можем да използваме следната формула на Диришле.

$$1+2\sum_{m=1}^M \cos(mx)=\frac{\sin((M+\frac{1}{2})x)}{\sin(\frac{x}{2})}$$

Изчисляваме

$$a(k)=\frac{1}{2}(\frac{\sin(\frac{2\pi(f_c+\frac{1}{2})k}{f_s})}{\sin(\frac{\pi k}{f_s})}-1), k=1,..., f_s-1$$

Отбелязваме, че конволюцията на две прости вълни с една и съща честота, но с амплитуда умножена по f_s / 2. Така, умножаваме филтъра по 2 / f_s. Отбелязваме също, че филтърът по-горе не може да бъде изчислен при k = 0, защото синусът в знаменателя ще даде нула. Използваме пак правилото на Лопитал. Също така изместваме филтъра така, че върхът му да е в средата.

$$a(k)=\begin{cases} \frac{1}{f_s}(\frac{\sin(\frac{2\pi(f_c+\frac{1}{2}) (k - \frac{f_s-1}{2})}{f_s})}{\sin(\frac{\pi (k-\frac{f_s-1}{2})}{f_s})}-1), k=1,..., f_s-1, k \ne \frac{f_s-1}{2} \\ \frac{1}{f_s} (2 (f_c+\frac{1}{2})-1), k=\frac{f_s-1}{2} \end{cases}$$

Накрая, този филтър е просто прекалено дълъг. Всяка проба в изходния сигнал с този филтър ще използва f_s изчисление. Предпочитаме един по-къс филтър с дължина N точки.

$$a(k)=\begin{cases} \frac{1}{f_s}(\frac{\sin(\frac{2\pi(f_c+\frac{1}{2}) (k - \frac{N-1}{2})}{f_s})}{\sin(\frac{\pi (k-\frac{N-1}{2})}{f_s})}-1), k=1,..., f_s-1, k \ne \frac{N-1}{2} \\ \frac{1}{f_s} (2 (f_c+\frac{1}{2})-1), k=\frac{N-1}{2} \end{cases}$$

Тази формула е приблизително изчисление на първата формула по-горе. При f_s = 2000 Hz, N = 101 и f_c = 40 Hz например амплитудните спектри на първия филтър по-горе (в синьо) и на филтъра тук (в червено) са почти еднакви.

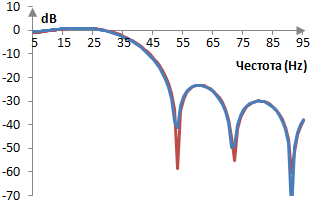
Вторият филтър всъщност е изведен с дискретизираното преобразуване на Фурие и затова е по-непрецизен.

Извеждане на нискочестотни филтри с неограничени импулсни спектри

Нискочестотните филтри с неограничени импулсни спектри също се извеждат от техните търсени амплитудни спектри. За един пример на това, как тези филтри се получават, виж темата Филтър на Батъруърт.