Филтъра на Батъруърт се дава от нормализираната трансферна функция
$$H(S)=\frac{1}{B_n(S)}$$
където n е разряда на филтъра и Bn(S) са нормализираните полиноми на Батъруърт
$$B_n(S)=\prod_{k=1}^{\frac{n}{2}}(S^2-2\,\cos(\frac{2k+n-1}{2n}\pi)S+1)$$ $$B_n(S)=(S+1)\prod_{k=1}^{\frac{n-1}{2}}(S^2-2\,\cos(\frac{2k+n-1}{2n}\pi)S+1)$$
съответно за n четно и нечетно.
Тази трансферна функция е нормализирана (т.е., тя е за нискочестотния филтър на Батъуърт с преходна честота 1). Ако заместим S = s / ωc, ще получим трансферната функция на нискочестотния филтър на Батъруърт, където ωc е преходната честота. Ако заместим S = ωc / s, ще получим високочестотния филтър на Батъруърт. Ако заместим S = (s2 + ωc2) / (B s), ще получим филтър на Батъруърт, който пропуска една честотна лента (средночестотен), като ωc е средата на тази честотна лента и B е ширината на лентата. Ако заместим S = B s / (s2 + ωc2), ще получим филтъра на Батъруърт, който спира една честотна лента (режекторен).
Пример: трансферна функция на нискочестотен филтър на Батъруърт от втори разряд
Ако използваме S = s / ωc и n = 2, ще получим трансферната функция
$$H(s)=\frac{1}{(\frac{s}{\omega_c})^2+\sqrt{2}(\frac{s}{\omega_c})+1}$$
По принцип, за всеки разряд n, трансферната функция на нискочестотния филтър на Батъруърт може да се изпише по следния начин.
$$H(s)=\frac{\omega_c^n}{\prod_{k=1}^{n}(s-s_k)}, \, s_k=\omega_c\,e^{\frac{j(2k+n-1)\pi}{2n}}$$
За да се изчислят цифровите или аналоговите Батъруърт филтри в детайли от тази трансферна функция, трябва да се използват доста алгебрични / математически манипулации. По принцип, съществуват два метода, примери за които са показани по-долу. Първият метод използва обратните преобразувания на Лаплас. Той изисква повече математически познания, но не изкривява честотния спектър на аналоговия филтър. Вторият метод използва билинейното преобразуване. Той е по-лесен и работи добре при цифровите филтри, въпреки че изчисленията са само приблизителни.
Пример на един импулсно инвариантен нискочестотен филтър на Батъруърт от втори разряд
Вземаме общата форма на трансферната функция на нискочестотния филтър на Батъруърт и заместваме n = 2. Трансферната функция става
$$H(s)=\frac{\omega_c^2}{(s-s_1)(s-s_2)}$$
Използваме определението за sk и развиваме с частичните дроби за да получим
$$H(s)=\frac{-j\frac{\omega_c}{2 \sin(\frac{3\pi}{4})}}{s-s_1}+\frac{j\frac{\omega_c}{2 \sin(\frac{3\pi}{4})}}{s-s_2}$$
Импулсният спектър може да се получи с обратното преобразуване на Лаплас. Аналоговия (в недискретно време) импулсен спектър е
$$y(t)=(-j\frac{\omega_c}{2 \sin(\frac{3\pi}{4})}e^{s_1 t}+j\frac{\omega_c}{2 \sin(\frac{3\pi}{4})}e^{s_2 t}) \, x(t)$$
където y(t) е изходния сигнал и x(t) е входния сигнал. Ако заместим t с k, ще получим дискретната форма на импулсния спектър. Преобразуването Z на импулсния спектър тогава е
$$H(z)=\frac{j \frac{\omega_c}{2 \sin(\frac{3 \pi}{4})}}{1-e^{s_1}z^{-1}}-\frac{j \frac{\omega_c}{2 \sin(\frac{3 \pi}{4})}}{1-e^{s_2}z^{-1}}$$
Комбинираме двете части и използваме факта, че s1 и s2 са спрегнати комплексни числа и че s1 s2 = ωc2 и s1+ s2 = 2 ωc cos(3π/4).
$$H(z)=\frac{-\frac{\omega_c}{\sin(\frac{3 \pi}{4})} \sin(\frac{\omega_c}{\sin(\frac{3 \pi}{4})}) \,e^{\omega_c \, \cos(\frac{3 \pi}{4})} z^{-1}}{1-2 \cos(\frac{\omega_c}{\sin(\frac{3 \pi}{4})}) \, e^{\omega_c \, \cos(\frac{3 \pi}{4})} z^{-1}+e^{2 \omega_c \, \cos(\frac{3 \pi}{4})} z^{-2}}$$
Нискочестотният филтър на Батъруърт от втори разряд тогава е
$$y(k)=-\sqrt{2} \omega_c \, \sin(\frac{\omega_c}{\sqrt{2}}) \, e^{-\frac{\omega_c}{\sqrt{2}}} x(k-1)$$ $$+2 \,\cos(\frac{\omega_c}{\sqrt{2}}) \, e^{-\frac{\omega_c}{\sqrt{2}}} y(k-1)-e^{-\sqrt{2}\,\omega_c} y(k-2)$$
където y(k) е изходния сигнал и x(k) е входния сигнал.
Да вземем например преходната честота ωc = 0.6. Трансферната функция става
$$H(z)=\frac{-0.22853 \, z^{-1}}{1-1.19249\,z^{-1}+0.42804\,z^{-2}}$$
и самият филтър се дава от
$$y(k)=-0.22853 \, x(k-1)+1.19249\,y(k-1)-0.42804\,y(k-2)$$
Следната графика показва изходния сигнал от филтъра след един импулс.
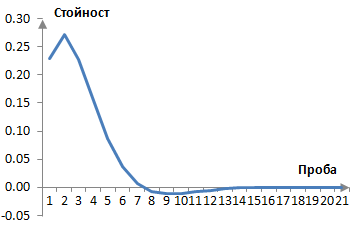
Ако пробната честота е, да кажем, 2000 Hz, тогава преходната честота е ωc = (0.6 * 2000 / (2 π)) = 191 Hz. Амплитудният спектър на този примерен филтър е показан в графиката по-долу.
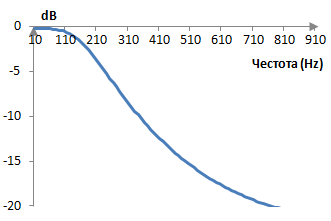
Пример на един нискочестотен филтър на Батъруърт от втори разряд с билинейното преобразуване
Един по-лесен начин да се изчисли трансферната функция на преобразуването Z на филтъра на Батъруърт е да се използва билинейното преобразуване. Връзката между преобразуването на Лаплас и преобразуването Z е z = esT, където T е времето на пробите (тоест, T= 1/ fs, където fs е пробната честота). Така
$$s=\frac{1}{T}ln(z) \approx \frac{2}{T} \frac{z-1}{z+1}$$
Използваме, както обикновено се предполага, T = 1 и заместваме s = 2 (z – 1) / (z + 1) за да получим
$$H(z)=\frac{a_0+a_1 z^{-1}+a_2 z^{-2}}{b_0+b_1 z^{-1}+b_2 z^{-2}}$$ $$a_0=\omega_c^2$$ $$a_1=2\omega_c^2$$ $$a_2=\omega_c^2$$ $$b_0=4-4\omega_c \, \cos(\frac{3 \pi}{4})+\omega_c^2$$ $$b_1=-8+2\omega_c^2$$ $$b_2=4+4\omega_c \, \cos(\frac{3 \pi}{4})+\omega_c^2$$
Да предположим пак, че преходната честота е ωc = 0.6 (в този случай, по принцип, ωc = 2 arctan(0.6/2) ≈ 0.583, заради изкривяването на честотния диапазон от билинейното преобразуване). След като използваме една и съща скаларна величина в знаменателя и числителя за да получим 1 в началото на знаменателя, имаме
$$H(z)=\frac{0.059435+0.118870z^{-1}+0.059435z^{-2}}{1-1.201904z^{-1}+0.439643z^{-2}}$$
Този филтър е различен от импулсно инвариантния филтър описан по-горе, защото билинейното преобразуване е приблизително. Следното са амплитудните спектри на двата филтъра.
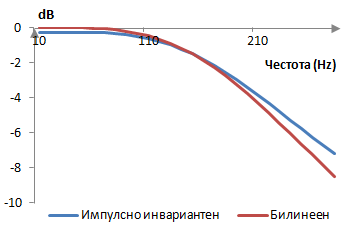
Филтърът след билинейното преобразуване работи по-добре и е по-лесен за изчисляване. Билинейното преобразуване обаче изкривява честотния спектър на филтъра. Един цифров филтър на Батъруърт с преходна честота ωd, ако е превърнат в аналогов филтър, че има преходната честота ωa = 2 tan(ωd/2) и, когато проектираме аналогови филтри, трябва да внимаваме да изберем правилната аналогова преходна честота. Така или иначе, билинейното преобразуване е по-лесния и по-често използвания метод.
Филтри на Батъруърт от по-високи разряди
Когато проектираме филтри на Батъруърт от по високи разряди, имаме избор. Можем да използваме методите показани по-горе. Тези методи изискват доста работа и доста изчисления. Другата възможност е да забележим, че корените sk на знаменателя на H(s) са двойки от спрегнати комплексни числа. При филтъра от разряд 4 например s1 и s4 образуват една спрегната двойка и s2 и s3 образуват друга спрегната двойка.
$$s_1=\omega_c \, e^{j \frac{5 \pi}{8}}$$ $$s_2=\omega_c \, e^{j \frac{7 \pi}{8}}$$ $$s_3=\omega_c \, e^{j \frac{9 \pi}{8}}=\omega_c \, e^{-j \frac{7 \pi}{8}}$$ $$s_4=\omega_c \, e^{j \frac{11 \pi}{8}}=\omega_c \, e^{-j \frac{5 \pi}{8}}$$
Можем да запишем H(s) за нискочестотния филтър на Батъруърт от четвърти разряд по следния начин.
$$H(s)=(\frac{\omega_c^2}{(s-s_1)(s-s_4)})(\frac{\omega_c^2}{(s-s_2)(s-s_3)})$$
И двете части имат реални коефициенти, защото използват комплексно спрегнати корени. Умножаването на две трансферни функции на два филтъра от разряд 2 означава, че импулсният спектър на сборния филтър е конволюцията на импулсните спектри на двата филтъра и филтрите трябва да бъдат подредени един след друг. Изходният сигнал на първият филтър дава входният сигнал на втория филтър (тези два филтри не са филтри на Батъруърт, защото корените sk не са този на филтъра на Батъруърт от разряд 2, но същите изчисления на билинейното преобразуване могат да се използват).
Следната графика сравнява амплитудните спектри на филтрите на Батъруърт от втори и четвърти разряд, като и двата филтъра са изчислени с билинейното преобразуване и като филтърът на Батъруърт е създаден като поредица от два филтъра от втори разряд. Забележи, че двата филтъра се пресичат при около -3 dB, което, типично за филтрите на Батъруърт, става при преходната честота. Тук пробната честота е пак 2000 Hz и преходната честота е ωc = (0.6 * 2000 / (2 π)) = 191 Hz.
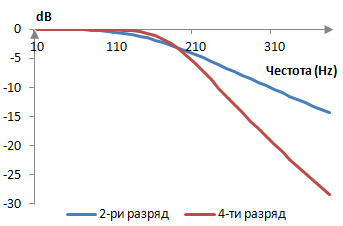
Пример на един високочестотен филтър на Батъруърт от втори разряд
Използваме S = ωc / s и n = 2 в трансферната функция най-отгоре в тази тема за да получим
$$H(s)=\frac{1}{(\frac{\omega_c}{s})^2+\sqrt{2}(\frac{\omega_c}{s})+1}$$
Това е трансферната функция на високочестотния филтър на Батъруърт от втори разряд. Използваме билинейното преобразуване s = 2 (z – 1) / (z + 1) за да превърнем тази трансферна функция в следната.
$$H(z)=\frac{4-8z^{-1}+4z^{-2}}{(\omega_c^2-2\sqrt{2}\omega_c+4)+(2\omega_c^2-8)z^{-1}+(\omega_c^2+2\sqrt{2}\omega_c+4)z^{-2}}$$
Когато ωc = 0.6 например, трансферната функция е
$$H(z)=\frac{0.6603-1.3208z^{-1}+0.6604z^{-2}}{1-1.2019z^{-1}+0.4396z^{-2}}$$
Взимаме например пробната честота 2000 Hz. Преходната честота тогава е ωc = 191 Hz и трансферната функция произвежда един филтър със следния амплитуден спектър.
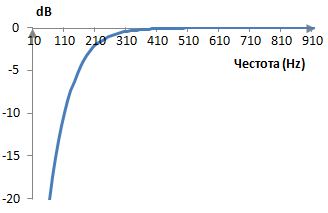
Пример на един средночестотен филтър на Батъруърт от втори разряд
Заместваме S = (s2 + ωc2) / (B s) и n = 2 за да получим средночестотния филтър на Батъруърт от втори разряд. Този филтър, а и филтъра на Батъруърт, който спира една честотна лента, изискват доста алгебрични операции и сигурно е по-лесно просто да се подредят нискочестотни и високочестотни филтри. Така или иначе, трансферната функция на средночестотния филтър на Батъруърт от втори разряд, след билинейното преобразуване, е следната.
$$H(z)=\frac{a_0+a_2z^{-2}+a_4z^{-4}}{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}+b_4z^{-4}}$$ $$a_0=4B^2$$ $$a_2=-8B^2$$ $$a_4=4B^2$$ $$b_0=16+8\sqrt{2}B+4(2\omega_c^2+B^2)+2\sqrt{2}B\omega_c^2+\omega_c^4$$ $$b_1=-64-16\sqrt{2}B+4\sqrt{2}B\omega_c^2+4\omega_c^4$$ $$b_2=96-8(2\omega_c^2+B^2)+6\omega_c^4$$ $$b_3=-64+16\sqrt{2}B-4\sqrt{2}B\omega_c^2+4\omega_c^4$$ $$b_4=16-8\sqrt{2}B+4(2\omega_c^2+B^2)-2\sqrt{2}B\omega_c^2+\omega_c^4$$
Ако използваме например ωc = 0.6 и B = 1 тогава филтърът е
$$H(z)=\frac{0.1132-0.2264z^{-2}+0.1132z^{-4}}{1-2.3789z^{-1}+2.3490z^{-2}-1.2136z^{-3}+0.3021z^{-4}}$$
Ако пробната честота например е 2000 Hz, тогава средата на лентата на пропускане е ωc = 191 Hz и ширината на тази лента е B = 318 Hz. Амплитудният спектър на този филтър е
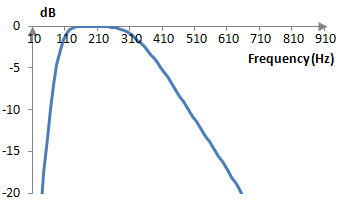
Идеята на Батъруърт и една лесна разработка на филтъра
Батъруърт е искал да създаде филтър, който има добро намаление на амплитудата в лентата на спиране и плосък амплитуден спектър в лентата на пропускане. Следното е търсеният амплитуден спектър (с малки промени) в оригиналната статия на Батъруърт.
$$|H(j\omega)|=\frac{G}{\sqrt{1+(\frac{\omega}{\omega_c})^{2n}}}$$
Ако предположим, че ω и ωc са нормализирани честоти и следователно са в честотния диапазон между 0 и π, тогава една графика на търсеният честотен спектър с ωc = 0.6 и при три различни стойности на n – 2, 5 и 8 – е тази, която е показана по-долу. Тази функция наистина може да представлява амплитудния спектър на един нискочестотен филтър – такъв, който има преходна честота от ωc и който става все по-добър с по-големи n.
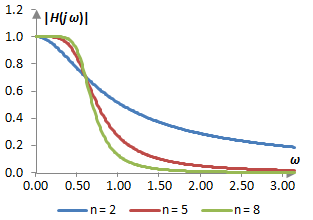
Отбелязваме, че амплитудния спектър на филтъра на Батъруърт намалява монотонно. Пьрвата производна на амплитудния спектър на филтъра на Батъруърт е
$$|H(j\omega)|'=((1+(\frac{\omega}{\omega_c})^{2n})^{-\frac{1}{2}})'=-n\,\omega^{2n-1}|H(j\omega)|^3$$
Тази производна е винаги отрицателна, понеже амплитудния спектър и честотите винаги са положителни. Това означава, че амплитудния спектър винаги намалява и няма вълни.
Ако продължим със следващите производни на амплитудния спектър, ще видим, че при ω = 0, всички производни до 2n-та производна са нула. Затова се казва, че този филтър има амплитуден спектър, който е максимално плосък.
Амплитудният спектър
$$|H(j\omega)|=\frac{G}{\sqrt{1+(\frac{\omega}{\omega_c})^{2n}}}=\frac{G}{\sqrt{1+(\frac{\omega^2}{\omega_c^2})^n}}$$
означава, че квадратът на трансферната функция, със s = j ω, трябва да бъде нещо като
$$H(s)^2=\frac{G^2}{1+(\frac{-s^2}{\omega_c^2})^n}$$
Можем да преработим квадрата на тази трансферна функция, като определим корените на знаменателя
$$1+(\frac{-s^2}{\omega_c^2})^n=0$$ $$s=\pm \omega_c \,e^{\frac{j(2k-1)\pi}{2n}}, \, k=1,2,...,2n$$ $$H(s)^2=G^2 \prod_{k=1}^{2n} \frac{1}{s-s_k}$$
Когато n = 2 например, знаменателят на квадрата на амплитудния спектър произвежда четири равно разпределени корени
$$s_1=\omega_c \, e^{j\frac{\pi}{4}}=\omega_c (\cos(\frac{\pi}{4})+j \, \sin(\frac{\pi}{4}))=(\frac{1}{\sqrt{2}}+j \frac{1}{\sqrt{2}})\omega_c$$ $$s_2=\omega_c \, e^{j\frac{3\pi}{4}}=(-\frac{1}{\sqrt{2}}+j \frac{1}{\sqrt{2}})\omega_c$$ $$s_3=-\omega_c \, e^{j\frac{\pi}{4}}=(-\frac{1}{\sqrt{2}}-j \frac{1}{\sqrt{2}})\omega_c$$ $$s_4=-\omega_c \, e^{j\frac{3\pi}{4}}=(\frac{1}{\sqrt{2}}-j \frac{1}{\sqrt{2}})\omega_c$$
Тук s1 и s4 са спрегнати комплексни числа и s2 и s3 са спрегнати комплексни числа. Тогава, когато n = 2
$$H(s)^2=\frac{G^2}{(s-s_1)(s-s_2)(s-s_3)(s-s_4)}$$
и
$$H(s)=\frac{G}{(s-s_a)(s-s_b)}$$
където sa и sb са някаква комбинация от два от четирите корена. (Обикновено, вместо да използваме H(s)2, изписваме H(s)H(-s). Предполагаме, че амплитудният спектър е симетричен спрямо нулата, от което има полза. Тъй като преобразуванията на Фурие, преобразуванията на Лаплас и преобразуванията Z използват синуси и косинуси, които са съответно отрицателни (sin(x) = -sin(-x)) и симетрични (cos(x) = cos(-x)) функции, обратните преобразувания на симетричния търсен амплитуден спектър обикновено ни позволява да произведем един филтър с реални коефициенти. Един такъв филтър понякога се нарича филтър с "нулева фаза". Тоест, ефектът на този филтър върху един сигнал зависи от честотата на сигнала, а не от фазата.)
Ако сме запознати с филтрите с неограничени импулсни спектри, ще вземем двата корена, които имат отрицателни реални части за да сме сигурни, че филтърът е стабилен (s2 и s3 по-горе). Следното е едно по-просто обяснение защо това има смисъл.
Тъй като предпочитаме една трансферна функция, която зависи от честотата на сигнала, а не от фазата, избираме, пак, sa и sb такива, че трансферната функция да стане функция с реални коефициенти. Това означава, че избираме два комплексно спрегнати корана. Отбелязваме също така, че комплексно спрегнатите двойки s1 и s4 и s2 и s3 произвеждат подобни, но малко различни функции със Z преобразованието, отбелязани с +/- в следната функция.
$$H(z)=\frac{-\sqrt{2}\omega_c \, \sin(\frac{\omega_c}{\sqrt{2}}) e^{\pm\frac{\omega_c}{\sqrt{2}}}z^{-1}}{1-2\,\cos(\frac{\omega_c}{\sqrt{2}})e^{\pm\frac{\omega_c}{\sqrt{2}}}z^{-1}+e^{\pm \sqrt{2}\omega_c}z^{-2}}$$
Двойката s1 и s4 всъщност дава
$$H(z)=\frac{-0.533888z^{-1}}{1-2.785910z^{-1}+2.33606z^{-2}}$$
Този филтър е нестабилен. Стойностите на изходните проби на този филтър ще започнат да се увеличават безкрайно, което може да се покаже ако просто към филтъра се изпрати който и да е синус или косинус.
Стабилността / нестабилността на тези филтри може също да се обясни, като се каже, че една стабилна система дава разумен (ограничен) изход при всеки разумен (ограничен) вход. Преобразуването на Лаплас на тази система трябва да е ограничено. Тъй като на практика се интересуваме само от неотрицателните амплитуди, искаме трансферната функция след преобразуването на Лаплас да е ограничена за всички s, за които ω = Re(s) ≥ 0. Ако трансферната функция има корени на знаменателя, при които тя няма да бъде ограничена, тогава тези корени трябва да имат отрицателни реални части.
Нискочестотният филтър на Батъруърт от втори разряд има четири потенциални корена, които са показани по-горе. Тези корени са показани и по-долу за ωc = 0.6 в равнината от комплексни s числа. Стабилният филтър може да бъде създаден, като се вземат двата корена с отрицателни реални части, които са двата корена в лявата част на равнината.
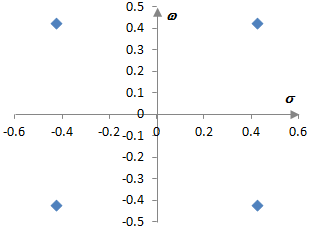
Добави нов коментар