I read a few articles about flangers vs. phase shifters and watched some videos. I found them unsatisfactory. It is hard to tell the difference. Many videos talk about more or less "whooshing", "bright", and "pronounced", but all of that means little to me and depends on the settings. Also, videos contradict each other.
Having designed flangers and phasers, I would say:
- The most pronounced part of a flanger is a vibrato with a slight tremolo and a bit of coloration.
- The most pronounced part of a phaser is a wah wah with coloration.
But don't trust me. Descriptions for these effects are often very different than mine. Just read more below.
Flanger
A flanger combines the original signal with a delayed copy of the original signal. The delayed copy is not decayed (i.e., it is at its original amplitude). The delay is very short (e.g., 5-20 milliseconds) and varies up and down at some rate (with some low frequency oscillation or LFO).
A simple delay
Check the combination of the original signal with the slightly delayed original signal, assuming the delay is constant. We will worry what happens when the delay varies below.
Here is a graph of the magnitudes of some frequencies, when combined with a delayed version of themselves. We use a short delay of 20 milliseconds.
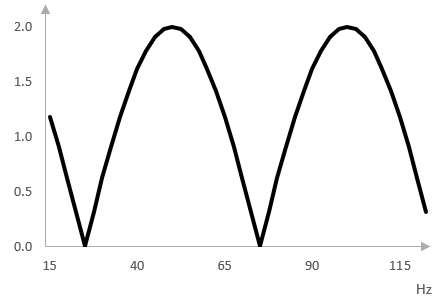
The amplitudes of the frequencies 50 Hz and 100 Hz are doubled. This makes sense. The period (cycle) of 50 Hz is 1 second / 50 = 0.02 seconds = 20 ms and so this wave is delayed by exactly its period. The delayed version is indistinguishable from the original. Adding the original and the delayed is the same as doubling the original wave.
Frequencies that are not multiples of 50 are reduced in magnitude by various amounts. The frequencies 25 Hz, 75 Hz, and so on are zeroed out. This also makes sense. The period of 25 Hz is 40 ms and so this wave is delayed by half of its period (it is inverted). The original wave, when combined with the same wave, but with inverted phase, gets zeroed out.
The graph looks like a comb, so the simple delay is a "comb filter". The position of the notches depends on the amount of delay.
The comb "colors" the sound. What is "coloration" anyway? I am using this term to say: The magnitude of frequencies that come out of the effect is not the same as the magnitude of frequencies that go in. Some are boosted, some are lowered, and so the signal is equalized in some fashion, but the term is fuzzy. What frequencies are affected how depends on the input, construction of effects, and settings.
A flanger
The flanger delay is not all. In a flanger, the delay varies slowly up and down.
When the delay varies, the delayed portion of the signal speeds up and slows down. This means that it changes pitch (higher pitch when sped up; lower pitch when slower).
When the pitch of the delayed signal changes (both up or down), the notches of the magnitude response of the graph slowly disappear.
- The solid line below shows the magnitude of frequencies in the combined original plus the delayed original signal with no change in pitch.
- The dashed line is the same, but with a slightly increased pitch in the delayed signal (approximately 7 cents, or 7 percent of a semitone).
- The dotted line is also the same an increase in pitch of approximately 40 cents (almost half of a semitone).
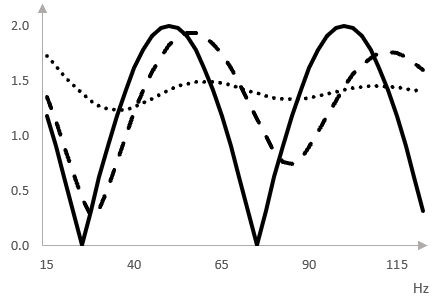
The larger the change in pitch (up or down), the flatter the magnitude response is.
What we hear in a flanger
In a flanger:
- The "notched" magnitude response is the "coloration". Again, the term is fuzzy, but this is the result of combining two out of phase signals and can be recognizable. It could give, for example, some metallic quality to a guitar recording. This is not the part I find most interesting.
- The fact that the notches appear and disappear (and actually move left and right) is also not an "aha" thing.
- The constant "detuning" and "re-tuning" of the delayed signal is noticeable. Essentially, this is a vibrato on the delayed signal. It is caused by the changes in delay which stretch and shrink the signal over time, thereby changing its pitch.
- Finally, as the notches of the flanger become flatter, the magnitude of the combined original and delayed signal decreases (for the pronounced frequencies in between notches). That is a slight tremolo.
For me, the most pronounced part of the flanger is the combined vibrato and tremolo.
Phaser
A phaser uses a sequence of all pass filters. The output of the first all pass filter is the input of the second all pass filter and so on. The output of the last all pass filter is combined with the original signal.
All pass filters
The following is one type of an all pass filter that can be used in a phaser. If the input and output signal at sample k are x(k) and y(k), then the filter is
$$y(k) = d * x(k) + x(k – 1) – d * y(k – 1)$$
The constant d is the "decay" of the filter (somewhere between 0 and 1). This is just an example and there are other types of all pass filters that can be used by a phaser.
A single all pass filter like the one above does not do much. It simply passes all frequencies, but with changes in phase.
When the filter output is combined with the original signal, the result is something of a low pass filter. Low frequencies are somewhat preserved and higher frequencies are somewhat attenuated. This is still not very interesting.
Things get interesting when we use more than one all pass filter.
A phaser
When the signal passes through two all pass filters, one after the other, and is then combined with the original signal, the resulting magnitude response is as in the graph below.
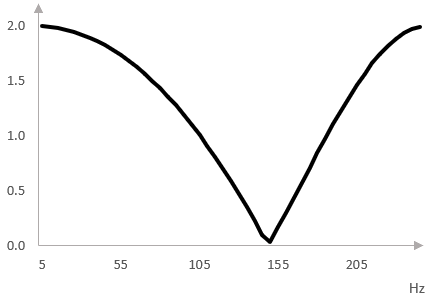
This is like a standard V equalizer. Low frequencies are preserved, high frequencies are preserved, the mids are dropped, creating a notch. Unlike the multiple notches of the flanger, there is one notch here.
Of course, phasers use more all pass filters. Adding two more all pass filters, for example, creates another notch. This means that a phaser does not always work like a V type equalizer – it does not always add brightness and bass. In fact, the last phaser I played with sounded quite the opposite – more mid rangy and less bright than my last flanger experiment.
The positions of the notches depend on the all pass filter decays. In the graph above, the decay of the first and second filters is 0.1 and 0.2.
Most importantly, when the decays of the all pass filters vary (up and down), the notch shifts (right and left respectively). It does not disappear.
Here is the graph when the decays are as in above (solid line), doubled (dashed line), and quadrupled (dotted line).
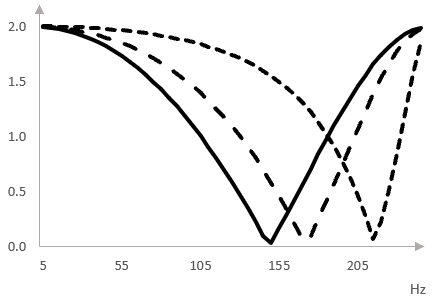
What we hear in a phaser
In a phaser:
- The shift of the notch left and right is similar to a wah wah.
For me, the most pronounced part of the phaser is exactly the wah wah quality.
Parameters
I am focusing on the movements of the flanger and phaser and not on the coloration. There is a reason for this – to hear just how the two effects differ, I use settings that make the movement very pronounced.
Both the flanger and the phaser can be rich in settings. The flanger can have the following parameters: frequency of oscillation in the delay, center of the delay, min and max delay (or pitch), gains on the original or delayed signal. The phaser can have: center of each all pass filter, frequency of oscillation of the filter decays, min and max for that oscillation, gains on the dry and wet signal.
It is easy to create settings where the movement in both effects is less noticeable than the coloration. The difference would then be harder to describe. But without the movement, a flanger will simply be s slapback delay and the phaser will simply become an equalizer. The movement is what makes these effects interesting.
authors: mic
Add new comment