An equalizer adjusts the magnitudes of selected frequency intervals in a signal.
An equalizer can, for example, increase or decrease the magnitude of high frequencies while leaving all the magnitude of other frequencies (low and mid-range ones) the same.
Examples of equalizers and sound samples
See Orinj Graphic equalizer, Orinj Parametric equalizer, and Orinj Simple equalizer to hear sound samples before and after an equalizer.
Equalization in practice
In practice, equalization typically involves reducing the magnitude of frequencies that are overwhelming in a mix or sound offending. Examples include frequencies:
- Below 80 Hz that create low frequency rumble.
- Between 100 Hz to 300 Hz that create boominess.
- Between 400 Hz to 500 Hz that create the impression that the sound is boxy (i.e., as if singing in a box).
- Between 1 kHz to about 2 kHz or, occasionally, up to 4 kHz that make vocals nasal.
- Between 5 kHz to 6 kHz that create too much sibilance ("s" sounds).
For example, to remove boominess in vocals, one can use an equalizer that is flat, except for a narrow band of frequencies somewhere between 100 Hz to 300 Hz. The magnitude of frequencies in that band is reduced and these "offending" frequencies thus become less audible.
The exact position and width of the band depend on the recording and requires experimentation (see also the discussion of Q factor below). The values above are simply guidelines. For some recordings, the offending frequencies can be outside of the bands listed above.
Occasionally, equalizing involves increasing the magnitude of frequencies. Examples include:
- Around 4 kHz or higher, above 5 kHz to add presence.
- Above 8 kHz to add "breathing room" and "air".
Reducing the magnitude of frequencies is usually done in very narrow bands to avoid making the recording hollow (see the discussion of Q factor below). Increasing the magnitude of frequencies is often done in wider bands. The exact parameters though depend on the recording and the preferences of the recording engineer.
Equalizer quality factor (Q factor)
The equalizer quality factor or "Q factor" describes how precise the equalizer is. The Q factor is the ratio of the midpoint frequency of the band that the equalizer is adjusting to the width of the same band.
For example, if the middle frequency is 200 Hz and width is 100 Hz, then the Q factor is 2. (The width of the band is typically measured at -3 dB. The choice of -3 dB is briefly described in the topic Butterworth filter).
Describing equalizers with a Q factor helps in practice. At higher midpoints of frequency bands, the same Q factor requires wider bands and wider bands are used at higher frequencies in practice.
For narrow bands when reducing frequencies, Q factors between 2 and 4 are typically used. For wider bands to increase frequencies, Q factors between 0.5 and 1 are typically used.
An example two-band digital equalizer
The following DSP example creates a two-band equalizer can be created. This example uses finite impulse response filters and has only two bands, which does not allow choosing narrow bands or Q factors, but is simple enough to show how equalizers can be created.
To create a two-band digital equalizer, we will combine a low pass filter and a high pass filter. The low pass filter will pass only low frequencies, below some cutoff frequency. The high pass filter will pass only high frequencies, above the same cutoff frequency. If we want to increase the magnitude of high frequencies, for example, we can add some gain to the high pass filter but not to the low pass filter and then combine the signals coming out of the two filters.
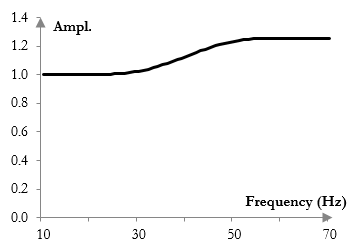
Take the sampling frequency 2000 Hz and create two filters of length 201. Use the cutoff frequency 40 Hz. Suppose that we add gain of 2 dB to the high pass filter, which means that we should multiply the coefficients of the high pass filter by 102/20 = 1.2589. Suppose that we use the Bartlett-Hann window, the magnitude response of which is somewhat smooth. Then the magnitude response of the total filter (the two-band equalizer) would be the one shown in figure below. This is an appropriate magnitude response for the desired equalizer.
The detailed steps to creating the equalizer are as follows.
- Create a finite impulse response low pass filter at 40 Hz (see Low pass filter).
- Create a finite impulse response high pass filter of the same length at 40 Hz or create a filter of different length and pad the shorter of the two filters with zeroes (see High pass filter).
- Multiply the coefficients of the high pass filter with the desired gain. The desired gain is 2 dB or 102/20 = 1.2589.
- Add the two filters together to obtain the equalizer.
If aL(k) are the coefficients of the low pass filter, aH(k) are the coefficients of the high pass filter, and g is the gain, then the total filter a(k) of the equalizer would be as follows.
$$a(k)=a_L(k)+g\,a_H(k)$$
The amount of gain applied to individual filters translates to the same amount of gain in the magnitude response of the total filter.
This is a two-band equalizer consisting of a low pass and a high pass filter and is quite simple. Multiband equalizers are just as simple. A three-band equalizer would need a low pass filter for the low frequency band, a band pass filter for the mid frequency band, and a high pass filter for the high frequency band. A ten-band equalizer would use one low pass filter, eight band pass filters, and one high pass filter.
To choose the appropriate cutoff frequencies for the filters, note that the human year interprets the frequency spectrum exponentially (e.g., the top of an octave is a note with frequency that is two times the frequency at the bottom of the octave). We should, split the frequency spectrum of a fixed band equalizer exponentially. If, for example, we are working with the frequency range of human hearing, say 20 Hz to 20000 Hz, we could create a ten-band equalizer by splitting this frequency range in 10 bands exponentially. The cutoff frequencies of the respective filters would be: 20 Hz = 20 * (20000 / 20)0/10, 39.9 Hz ≈ 20 * (20000 / 20)1/10, 79.6 Hz ≈ 20 * (20000 / 20)2/10, and so on until 20,000 Hz = 20 * (20000 / 20)10/10.
Add new comment