The Shroeder-Moorer filter is given by the transfer function
$$H(z)=\frac{1-d\,z^{-1}}{1-d\,z^{-1}-f\,(1-d)\,z^{-N}}$$
where d and f define the comb filter decay as described below and N is the comb filter delay.
The Shroeder-Moorer filter is usually called a low pass feedback comb filter. Given a discrete input signal x(k), the impulse response equation that corresponds to the transfer function above computes the output signal y(k) as follows.
$$y(k)=x(k)-d\,x(k-1)+d\,y(k-1)+f\,(1-d)\,y(k-N)$$
A graphical representation of the impulse response of the Shroeder-Moorer filter with f = 0.84, d = 0.5, and N = 20 is shown below.
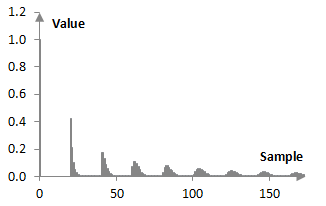
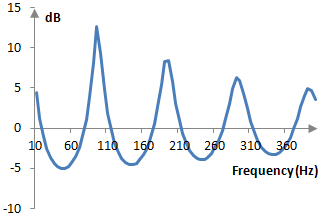
The magnitude response of the filter is the characteristic feedback comb, except that the comb ripples are not of constant magnitude, but are slowly decreasing. The following is the magnitude response of the filter above at the sampling frequency of 2000 Hz.
Using the Shroeder-Moorer filter
Several Shroeder-Moorer filters can be used in combination with several Shroeder all pass filters to simulate late reverb. Typically, the input signal would be fed through several parallel Shroeder-Moorer filters and then through several consecutive stacked all pass filters. The impulse responses of the Shroeder-Moorer filters are such that they add irregularities to the late reverb, which are similar to the irregularities that Shroeder observed in natural reverb. The all pass filters add diffusion through multiple repetitions of the signal.
A larger d produces irregularities of smaller amplitude and more smoothly transitioning from one to the other. A larger f produces larger irregularities. A larger N increases the number of samples between irregularities.
When the Shroeder-Moorer filter is used to simulate late reverb, typical values for the filter parameters are approximately f = 0.8 and d = 0.2. The values of N depend on the sampling rate, but usually N is such that it translates to about 100-150 milliseconds. Since several Shoeder-Moorer filters are used when simulating reverb, the parameters are chosen such that the repetitions of the different filters do not coincide very often. For example, the different values for N are chosen such that they are mutually prime.
Comments
His name is in fact Moorer,
His name is in fact Moorer, not Moore.
Fixed it
Thanks. It is fixed. I am not sure how this happened
Add new comment