Distortion

In music, distortion is the sound effect that occurs when the amplitude peaks of a signal are compressed or cut off when the audio equipment is overloaded.

Example distortion and sound sample

See Orinj Distortion to hear a sound sample before and after distortion.

Types of distortion

There are various types of distortion. The signal peaks may be cut off, which is called a clip or a hard-clip. The signal peaks can be compressed and then cut off, which is called a soft clip (see below). Or, the signal peaks may be simply compressed. In music, the type of distortion described here is usually intentional (whereas outside of music it is usually unwanted) and is sometimes called overdrive.

More generally, this type of distortion will occur whenever the underlying wave form of the signal is changed because the amplitude of the signal is being changed too quickly. A compressor with very fast attack and release, for example, may introduce distortion.

Aural exciter

An aural exciter is a distortion effect that uses a high pass filter to separate and distort only high frequencies. See Orinj Aural exciter to hear a sound sample before and after an aural exciter.

Distortion staging

Any one operation above will introduce distortion, but that distortion may not be very audible. Several such operations applied in sequence, called the distortion stages, will produce audible distortion. Two-stage distortion can, for example, use two soft clippers in sequence or a soft clipper first and a hard clipper second, where the second distortion stage uses a lower threshold than the first distortion stage.

Digital distortion

The following is an example of a hard-clip distortion:

$$y(k)=\begin{cases} 0.75 & |x(k)| \ge 0.75 \\ x(k) & |x(k)| \lt 0.75 \end{cases}$$

The result of using this type of distortion on a signal is as follows.

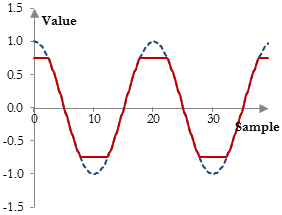
The signal peaks are simply cut off.

The following is an example of a soft-clip distortion (known as the cubic soft clipper).

$$y(k)=\begin{cases} -(w-\frac{w^3}{3}), & x(k) \lt -w \\ x(k)-\frac{x(k)^3}{3}, & |x(k)| \le w \\ (w-\frac{w^3}{3}), & x(k) \gt w \end{cases}, w \gt 0$$

With larger w, the clipping becomes softer and closer to the peak of the wave. The result of using this distortion on a signal is as follows.

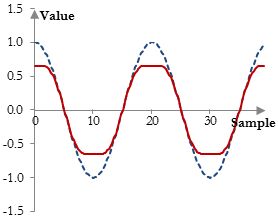
The following is an example of distortion that compresses the signal peaks, but does not clip them.

$$y(k)=\mathrm{atan}(x(k))$$

Distortion and harmonics

Any non-linear modification of the signal will introduce harmonics. What is interesting about all digital distortions above, however, is that they introduce odd order harmonics. This should not be a surprise, as compressing the peaks of a signal is almost the same as introducing the first odd order harmonic of the signal (at three times the original frequency) with a lower amplitude as in the graph below. This graph shows the original signal (dotted line) and a signal that is the sum of the original signal and its first odd order harmonic.

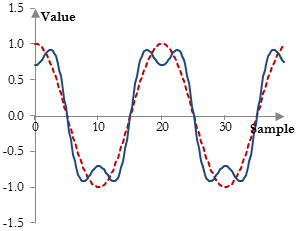
It is, in fact, almost impossible to introduce anything but odd order harmonics into a signal through distortion. If we introduce even order harmonics, we will note an expansion in the signal peaks, rather than compression. The following graph, for example, shows the sum of the original signal and its first even order harmonic.

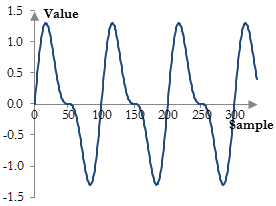
To introduce even order harmonics, we need to look at operations that expand the signal peaks rather than compress them, which is not distortion as defined here. Example such operations are:

$$y(k)=x(k)^3$$

and

$$y(k)=\begin{cases} x(k), & x(k) \gt x(k-1) \\ x(k)^3, & x(k) \le x(k-1) \end{cases}$$

The first introduces both even and odd order harmonics. The second introduces only even order harmonics, except for the first odd order harmonic.

Distortion outside of music production

The term distortion has different meanings outside of music production. The type of distortion above may be a special case of amplitude distortion, as the amplitude of the output signal is not a linear function of the amplitude of the input signal, although this depends on how we measure amplitudes. Digital signal processing filters (see, for example, Low pass filter), introduce frequency distortion, as the amplitude or magnitude of output frequencies is different than the amplitude of input frequencies (i.e., the filter has a magnitude response). To the extent that an operation on a signal introduces harmonics, it is called harmonic distortion.