Преобразуване Z

Двустранното преобразуване Z е

$$Z(x(k))=\sum_{k=-\infty}^{\infty} x(k) \, z^{-k}$$

където z = A e^{-j ω} за някакво реално число A.

Мотивация за използването на преобразуването Z при работата с цифрови сигнали

Преобразуването Z е едно обобщение на преобразуването на Фурие в дискретизирано време, което се дава от

$$H(\omega)=\sum_{k=-\infty}^{\infty} x(k) \, e^{-j \, \omega \, k}$$

Както с другите преобразувания на Фурие, преобразуването на Фурие в дискретизирано време превежда един сигнал x(k), който е функция на времето с комплексни стойности, в множество от комплексни числа, които носят честотата и фазата на всяка от простите вълни в сигнала. Преобразуването на Фурие в дискретизирано време се използва, когато x(k) е дискретизиран, но не е определен само в ограничен интервал и не е периодичен (в другите случаи могат да се използват преобразуването на Фурие или дискретизираното преобразуване на Фурие). Преобразуването на Фурие в дискретизирано време е един логичен резултат от дискретизирането във времето на (вземането на проби) на входния сигнал x(t) в преобразуването на Фурие.

Двустранното преобразуване Z обобщава преобразуването на Фурие в дискретизирано време, като въвежда реалното число A, което представлява амплитудата на базата A e^{-j ω k} на преобразуването.

$$H(\omega)=\sum_{k=-\infty}^{\infty} x(k) \, z^{-k}=\sum_{k=-\infty}^{\infty} x(k) \, A \, e^{-j \, \omega \, k}$$

Също така, преобразуването на Фурие в дискретизирано време е просто преобразуването Z с A = 1. Когато A = 1, базата на преобразуването се състои от числата e^{-j ω k}, които в равнината на комплексните числа образуват един кръг с радиус 1 около началото. Така, можем да кажем, че преобразуването на Фурие в дискретизирано време е просто преобразуването Z, изчислено върху кръга единица.

Мотивацията за използването на преобразуването на Фурие в дискретизирано време при работата с цифрови сигнали е, че ни позволява да използваме един дискретизиран сигнал, но недискретизирани честотни и фазови диапазони. Мотивацията за използването на преобразуването Z при работата с цифрови сигнали, вместо преобразуването на Фурие в дискретизирано време, е само това, че нотацията е по-малко. Всъщност, при работата с цифрови сигнали, винаги ще използваме преобразуването Z върху кръга единица – с A = 1 – което означава, че всъщност ще използваме само преобразуването на Фурие в дискретизирано време и никога няма да използваме неговата обобщение – преобразуването Z. Ще използваме, обаче, нотацията на преобразуването Z. По-лесно е да напишем z^-k вместо e^{-j ω k}.

Някои полезни свойства на преобразуването Z

Едно от полезните свойства на преобразуването Z е, че е линейно подобно на преобразуванията на Фурие.

$$Z(a_1 x_1(k) + a_2 x_2(k))=a_1 Z(x_1(k))+a_2 Z(x_2(k))$$

Второ, изместването на сигнал x(k) във времето ни дава следното.

$$Z(x(k-m))=\sum_{k=-\infty}^{\infty} x(k-m) \, z^{-k}$$ $$=\sum_{k=-\infty}^{\infty} x(k-m) z^{-(k-m)} z^{-m}=Z(x(k)) \, z^{-m}$$

Това означава, че, ако изхода от системата a(k) при входа x(k) се дава от

$$y(k)=\sum_{n=0}^{N-1} a(n) \, x(k-n)$$

което пък означава, че a(k) може да е един филтър с ограничен импулсен спектър, тогава

$$Z(y(k))=Z(\sum_{n=0}^{N-1} a(n) \, x(k-n))=(\sum_{n=0}^{N-1} a(n) \, z^{-n}) Z(x(k))$$

и

$$H(z)=\frac{Z(y(k))}{Z(x(k))}=\sum_{n=0}^{N-1} a(n) \, z^{-n}$$

което е трансферната функция на системата a(k). Тази трансферна функция има интересни характеристики. При линейни системи, които са инвариантни спрямо времето, амплитудата |H(z)| на H(z), z = A e^{-j ω}, когато е изчислена с A = 1 (върху кръга единица), дава амплитудния спектър на системата

$$|H(e^{-j \, \omega})|=\sqrt{Re(H(e^{-j \, \omega}))^2+Im(H(e^{-j \, \omega}))^2}$$

Фазовият спектър на системата е

$$\Phi(e^{-j \, \omega})=\mathrm{atan2}(\frac{Im(H(e^{-j \, \omega}))}{Re(H(e^{-j \, \omega}))})$$

Използваме нотацията |H(e^{-j ω})| и Φ(e^{-j ω}) за да покажем, че амплитудният спектър и фазовият спектър са изчислени с e^{-j ω}, а не със z = A e^{-j ω}.

Примерна трансферна функция на един гребенов филтър с преобразуването Z

Един напредващ гребенов филтър е просто един прост дилей. Този филтър използва изчислението

$$y(k)=x(k)+g \, x(k-m)$$

където g е промяна в амплитудата, 1 – g е затихването на забавения сигнал и m е забавянето в брой проби. Преобразуването Z на двете страни на уравнението по-горе дава

$$Z(y(k))=Z(x(k)+g \, x(k-m))=Z(x(k))+g \, z^{-m} Z(x(k))=Z(x(k))(1+g \, z^{-m})$$

Трансферната функция на този гребенов филтър тогава е

$$H(z)=\frac{Z(y(k))}{Z(x(k))}=1+g \, z^{-m}$$

Амплитудният спектър на гребеновия филтър за някаква определена честота ω е

$$H(e^{-j \, \omega})=|1+g \, z^{-m}|=|1+g \, e^{-j\, \omega \, m}| = |1+g \, \cos(\omega \, m)-g \, \sin(\omega \, m)| $$ $$= \sqrt{(1+g \, \cos(\omega \, m))^2+(g \, \sin(\omega \, m))^2}= \sqrt{(1+g)^2+2 \, g \, \cos(\omega \, m)}$$

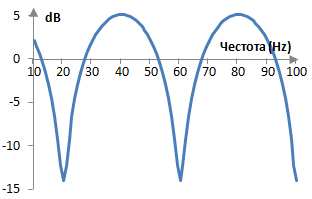
Тази функция на ω, като графика, дава характерният амплитуден спектър на филтъра, който наподобява един гребен, както по-долу. Този примерен напредващ гребенов филтър бе изчислен с пробната честота f_s = 2000 Hz, забавянето m = 50 проби и с g = 0.8.

Други примери

За други примери за използването на преобразуването Z, виж темите Гребенов филтър, Трансферна функция, Феномен на Гибс, Филтър на Батъруърт, Всичкопропускащ филтър и Филтър на Шрьодер и Муурър.