На практика, звукът е едно сложно множество от вълни с различни честоти, фази и амплитуди. Когато звукът е записан цифрово обаче, той става просто една поредица от числа. Характеристиките на многото звукови вълни – честота, фаза, амплитуда – не могат да се забележат в цифровите данни. При работата с аудио тогава:
Преработката на цифрови сигнали (от англ., "digital signal processing" или DSP) е науката за манипулирането на цифрови сигнали като се използва нищо повече от това, което се съдържа в цифровия запис на сигнала и без да се знаят неговите точни характеристики.
Един цифров аудио сигнал е просто поредица от числа и операциите, които променят тези числа, трябва да са математически по естество. DSP манипулира цифровите сигнали обикновено с математически операции. Това е една наука с широк обхват и с приложения не само в музиката и математиката, но и във физиката, инженерството, фотографията, видеото и много други. DSP, всъщност, е с толкова голям обхват, че определението по-горе не е достатъчно прецизно. За целите тук обаче е подходящо.
Следното е едно просто въведение към DSP с примери на прости операции DSP.
Характеристики на простите вълни и математическото представяне на сложните сигнали
Вълната
$$x(t)=A\,\cos(2\pi\,f\,(t-\tau))$$
има начална фаза равна на τ единици от време, амплитуда на върха равна на A, честота равна на f цикли в една единица от време и дължина на цикъла равна на 1/f единици от време. Трите характеристики – амплитуда, фаза и честота (или дължина на цикъла) – напълно определят една проста косинус вълна като функция на времето.
Когато тази вълна е записана цифрово, стойността и е записана в различни точки във времето. Този процес е процеса на вземането на проби или семпли (на англ., "sampling"). Броят на пробите в един интервал във времето се нарича пробна честота. Обикновено, пробите се вземат на равни интервали във времето и пробната честота е една константа. Също така е нормално пробите да се записват със сравними амплитуди, наречени пробна резолюция. Процесът на вземане на проби с постоянна пробна честота и резолюция опростява DSP и се нарича pulse code modulation или PCM.
Предположи, че вземаме проби от простата вълна A cos(2π f (t – τ)) в един интервал във времето T с пробната честота fs. Точките във времето на пробите са t = 0, 1/fs, 2/fs, 3/fs и така нататък. Ако тези проби се отбележат с k = 0, 1, 2, …, тогава стойността на вълната при всяка проба ще е
$$x(k)=A\,\cos(2\pi\,f\,(\frac{k}{f_s}-\tau))$$
При τ секунди, ще имаме m ≈ τ / T = τ fs проби и така, приблизително, можем да запишем горната формула и по следния начин.
Ако пробната честота е fs, вълната
$$x(k)=A\,\cos(\frac{2\pi\,f\,(k-m)}{f_s})$$
има начална фаза m проби или m / fs единици във времето, амплитуда на върха A и честота f. Цикълът и е 1/f единици във времето или fs / f проби. Пак, трите характеристики – амплитуда, фаза, честота – напълно определят тази косинус вълна като функция на времето. (Забележи тук една от най-важните теореми в DSP – теоремата за дискретизацията. В една от многото си версии, теоремата казва, че честотното съдържание на един сигнал е напълно представено от една пробна честота, ако сигналът не съдържа честоти по-високи от половината от пробната честота. Тоест, само вълни с честоти до половината от една опредлена пробната честота могат да се запишат цифрово с тази пробна честота.)
Често мислим за практичните сигнали като за суми от много прости вълни. Един сложен сигнал в непрекъснато време x(t) може да бъде следния.
$$x(t)=\sum_{n=0}^{N-1} A_n\,\cos(2\pi\,f_n\,(t-\tau_n))$$
An, fn и τn са амплитудите на върха, честотите и началните фази на всеки от n-те прости вълни в сигнала.
Един сложен сигнал в дискретизирано време x(t), при пробната честота fs, ще е
$$x(k)=\sum_{n=0}^{N-1} A_n\,\cos(\frac{2\pi\,f_n\,(k-m_n)}{f_s})$$
При работата с цифровите сигнали, ще работим със сигнали, за които не знаем точните стойности на N, An, fn и mn или τn. Както по-горе, задачата на DSP е да манипулира x(k) без да знае тези стойности.
Сигналът в следната графика например съдържа три прости вълни. Можем да забележим, че сигналът поне съдържа една по-висока честота с по-малка амплитуда и някакви по-малки честоти. Не е възможно обаче да знаем, че това се точно простите вълни cos(t), cos(0.5 t) и 0.4 cos(2π t).
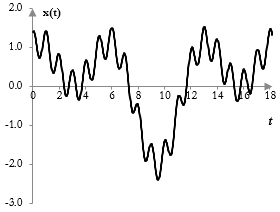
Сигналите на практика
Един основен въпрос остава: Дали всички сложни сигнали се състоят от прости вълни. Всъщност, не знаем дали сигналите на практика са подобни на синусоиди.
Оказва се, че дали сигналите на практика са суми на прости вълни, не е важно. В 1807, Джоузеф Фурие показва, че всяка периодична функция с период 2π, която може да се интегрира въру [-π, π] може да бъде изразена приблизително с една (потенциално безкрайна) линейна сума от синуси и косинуси (виж Анализ на Фурие). С малки промени в теорията на Фурие, подобни приближения могат да бъдат изчислени за други периоди и интервали. Можем да продължим да работим със сложните сигнали все едно са суми от прости вълни, независимо дали са на практика.
Прости операции DSP
Смесването на музика – комбинирането на няколко писти с аудио в една – е една от най-простите операции в DSP. Вземи един запис на четири писти, които още не са смесени: барабани, бас, китара и вокали. Всяка писта съдържа пробите на един сигнал и имаме четири сигнала, които ще отбележим с xd(k), xb(k), xg(k) и xv(k) съответно за барабаните, баса, китарата и вокалите. Можем да смесим тези писти в едно музикално парче, ако всички писти са записани с една и съща пробна честота и ако приемем, че амплитудите, панорамите, обвивките и различните ефекти за тези писти вече са приложени и не трябва да се правят допълнителни настройки. Изходният сигнал от смесването y(k) е сигнала
$$y(k)=x_d(k)+x_b(k)+x_g(k)+x_v(k)$$
Най-простият дилей в DSP е този, при който сигналът е повторен веднъж с някакво забавяне и с някакво затихване. Изходният сигнал y(k) на простия цифров дилей може да бъде изчислен със следното уравнение.
$$y(k)=x(k)+A\,x(k-m)$$
Изходният сигнал y(k) е сумата на оригиналния входен сигнал x(k) и същия входен сигнал x, но този път забавен с m проби и с амплитуда умножена по A. Ако пробната честота е fs, забавянето от m проби е еквивалентно на забавяне от m / fs единици във времето. Тази операция също така се нарича напредващ гребенов филтър.
Вземи следното изчисление на изходния сигнал y(k) от входния сигнал x(k).
$$y(k)=\begin{cases} 0.75, & |x(k)| \ge 0.75 \\ x(k), & |x(k)| \lt 0.75 \end{cases}$$
Това е дисторшън с "твърдо окастряне" (от англ., "hard clip").
По-сложни операции DSP
Простите операции в DSP по-горе не използват факта, че сложните сигнали се състоят от прости синусоиди. По-сложните операции в DSP използват този факт.
Повечето сложни операции в DSP използват два прости факта. Първо, сумата на произведението (и конволюцията) на две прости вълни с различни честоти е нула при правилно избрани интервали (т.е., простите вълни са ортогонални). Второ, сумата на произведението (и конволюцията) на две прости вълни с една и съща честота е константа при правилно избрани интервали. Това прави намирането на прости вълни в сложния сигнал, а и тяхната амплитуда и фаза, лесно. Това е обяснено в темата Анализ на Фурие. Сравнително прости примери на приложението на тези факти е алтернативното извеждане на нискочестотния филтър и интерпретацията на преобразуването на Фурие в този сайт.
Разбира се, не всичко в DSP зависи от тези два факта. Виж например компресирането на данни в цифровите сигнали с вълничките на Хаар или вълничките Daub4. Забележи обаче, че самите вълнички имат същите свойства – те са ортонормални – и също така могат да действат като нискочестотни и високочестотни филтри върху сигнала.
Добави нов коментар