Един високочестотен филтър е честотен филтър, който позволява (пропуска) честотите над някаква преходна честота и не позволява (спира) честотите под тази преходна честота.
Пример на един високочестотен филтър със звуково парче
Виж Orinj Високочестотен филтър за да чуеш едно звуково парче преди и след един високочестотен филтър.
Идеален амплитуден спектър на един високочестотен филтър
Следната графика показва амплитудния спектър на един идеален високочестотен филтър.
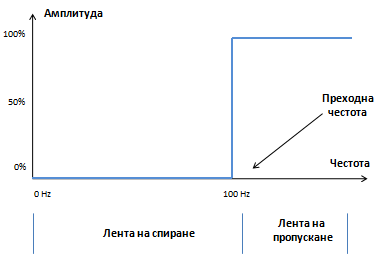
Всички честоти над преходната честота остават със своята начална амплитуда. Всички честоти под преходната честота са напълно премахнати.
Работа с високочестотните филтри при смесването на музика
Високочестотните филтри се използват често при смесването на музика. Могат да се използват да разделят инструментите в честотния диапазон (т.e., да направят така, че различните инструменти да заемат различни части от честотния диапазон). Например, един високочестотен филтър с преходна честота от около 300 Hz или повече над една китарна писта може да помогне да се отдели китарата от баса. Високочестотни филтри с по-високи преходни честоти могат по същият начин да разделят две китари или които и да е други инструменти.
Един високочестотен филтър с много ниска преходна честота (например 40 Hz) може да се използва да махне ниските честоти от баса или може би и от касата за да предотврати мътността или уморяването на ушите в смесеното.
Пример: Цифров филтър с ограничен импулсен спектър
Вземи например един цифров филтър w(k), който изчислява изходния сигнал y(n) от входния сигнал x(n) с формулата
$$y(n)=\sum_{k=0}^{N} w(k)\,x(n-N+k)$$
с тежести изчислени по следната формула.
$$w(k)=\begin{cases} -\frac{\sin(2\pi \frac{f}{f_s}(k-\frac{N-1}{2}))}{\pi (k-\frac{N-1}{2})}, k \ne \frac{N-1}{2} \\ 1-2\frac{f}{f_s}, k=\frac{N-1}{2} \end{cases}$$
Тук fs е пробната честота, N е дължината на филтъра (броя на членовете в сумата), w(k) са тежестите на филтъра и f е някаква честота между 0 и fs / 2. Този филтър е високочестотен филтър с преходна честота f, защото той пропуска честотите над f и понижава амплитудата на честотите под f.
Ако например fs = 2000 Hz, f = 40 Hz, и N = 201, тогава амплитудният спектър на филтъра ще бъде както в графиката по-долу.
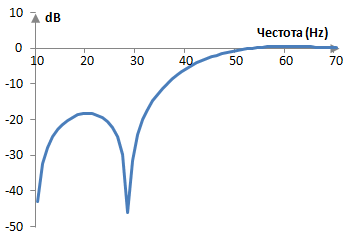
Въпреки че амплитудният спектър на този филтър не е идеален, този филтър пропуска честотите над 40 Hz почти непроменени и понижава амплитудите на честотите под 40 Hz. Следователно, това е един високочестотен филтър с преходна честота 40 Hz.
Има няколко разлики между този филтър и идеалния филтър.
- Честотите, които трябва да са спрени, не са напълно спрени. В тази честотна лента – лентата на спиране – амплитудата на тези честоти намалява, но само с около -20 dB.
- В лентата на спиране и в лентата на пропускане, амплитудният спектър не е плосък, а има вълни (виж Феномен на Гибс).
- Амплитудният спектър на филтъра на минава от лентата на спиране към лентата на пропускане рязко, а го прави плавно. Така, има една преходна лента от честоти.
Ако дължината на филтъра се увеличи, смаляването на амплитудите в лентата на спиране се подобрява, преходната лента намалява (прехода е по-бърз) и размера на вълните намалява.
Извеждане на високочестотния филтър с ограничен импулсен спектър
Високочестотният филтър по-горе може да се изведе, като се обърне един нискочестотен филтър.
- Виж Нискочестотен филтър за обяснение на това, как се извежда един нискочестотен филтър с ограничен импулсен спектър.
- Знаем, че един нискочестотен филтър с ограничен импулсен спектър и с коефициенти, които са симетрични спрямо средата, както този нискочестотен филтър, ще даде едно постоянно забавяне във фазите на честотите в сигнала (виж Фазов спектър).
- Създаваме един всичкопропускащ филтър, които пропуска всички честоти с непроменена амплитуда, но който също е един филтър с ограничен импулсен спектър и с коефициенти, които са симетрични спрямо средата. Този филтър ще произведе същото забавяне във фазата, както нискочестотния филтър. Всичкопропускащият филтър е 0, 0 …, 0, 1, 0, 0, …, 0, с дължина равна на дължината на нискочестотния филтър.
- Изваждаме изходният сигнал от нискочестотния филтър от изходния сигнал на всичкопропускащия филтър. Всичкопропускащият филтър пропуска всички честоти. Нискочестотният филтър пропуска ниските честоти. Разликата е високите честоти. Това работи само защото забавянето във фазата е едно и също и при двата филтъра.
- Отбелязваме също, че, тъй като изчислението на филтрите върху сигнала е линейно, вместо да изваждаме изходните сигнали от филтрите, можем да извадим коефициентите на филтрите.
Резултатът е филтъра, показан по-горе.
Високочестотни филтри с неограничени импулсни спектри
Примери на високочестотни филтри с неограничени импулсни спектри са дадени в темите Филтър на Бесел. Филтър на Батъруърт, Филтър на Чебишев (първи вид), Елиптичен филтър.
Добави нов коментар