Фазовият спектър на едно оборудване или софтуер е математическо, числено или графично представяне на разликата между фазите на изходния сигнал и входния сигнал на това оборудване или софтуер.
Терминът фаза може да има няколко значения, но за нашите цели тук фазата на една вълна е, да кажем, отместването на началото на цикъла на вълната от началото на времето. Една вълна с честота f например може да бъде записана като sin(2 π f t), където t е времето. Вълната започва със стойността нула, защото при t = 0 имаме sin(0) = 0. Вълната завършва един пълен цикъл между t = 0 и t = 1 / f и при t = 1 / f имаме sin(2 π) = 0. Тъй като цикъла на вълната отнема 1 / f единици на време, в една единица време вълната ще завърши f цикъла. Вълната тогава има честота f. Цикълът на тази вълна започва при 0. Ако искаме да отместим вълната, можем да използваме
$$\sin(2 \pi f (t - T))$$
където T е някаква константа от определено време. Тази вълна започва своя цикъл при t = T и следователно можем да наречен T фазата на вълната. От друга страна пък, а и по-често, можем да запишем вълната като
$$\sin(\omega t – \theta)$$
където ω е ъгловата честота ω = 2 π f и θ е ъгловата фаза θ = 2 π f T. В този случай, отместването на началото на цикъла на вълната е представено като размера на един ъгъл (т.е., в радиани). Тъй като вълната завършва един цикъл за 2 π, тогава една фаза от θ = π например определя, че фазата е равна на половината от цикъла на вълната.
Обикновено, фазовият спектър е промяната във фазата в радиани за различни честоти в честотния диапазон. Да предположим, че входната вълна в някакво оборудване или софтуер е sin(2 π f (t - T1)) и че изходната вълна е sin(2 π f (t - T2)). Можем да кажем, че промяната във фазата е забавянето във времето между двете вълни от T2 – T1. Можем също така да кажем, че, понеже вълната има цикъл от 1 / f единици на времето, тази вълна ще бъде забавена с f (T2 – T1) части от своя цикъл, което е 2 π f (T2 – T1) радиани. Подобно, ако ω е ъгловата честота ω = 2 π f и фазите са θ1 = 2 π f T1 и θ2 = 2 π f T2, тогава двете вълни са sin(ω – θ1) и sin(ω – θ2) и фазовият спектър е
$$(\theta_2 – \theta_1) = 2 \pi f (T_2 – T_1)$$
Защо е важна фазата?
Да вземем две синусоиди с една и съща честота f, но с различни фази T1 и T2, например sin(2 π f (t-T1)) и sin(2 π f (t-T2)). Знаем, че
$$\sin(2 \pi f (t-T_1)) + \sin(2 \pi f (t-T_2)) $$ $$ = 2 \sin(\frac{2 \pi f (t-T_1)+ 2 \pi f (t-T_2)}{2}) \cos(\frac{2 \pi f (t-T_1)- 2 \pi f (t-T_2)}{2}) $$ $$ = 2 \sin(2 \pi f (t-\frac{T_1+T_2}{2}) \cos(2 \pi f \frac{T_2-T_1}{2})$$
Това означава, че когато тези две вълни са събрани, резултатът е синусоида със същата честота, но с фаза (T1+T2) / 2 и с амплитуда равна на амплитудата на оригиналните вълни, умножена по 2 cos(2 π f (T2-T1) / 2). С други думи, когато две вълни с една и съща честота са събрани, се получава вълна със същата честота, но с амплитуда, която зависи от двете фази и от самата честота. В крайния вариант, когато двете фази са равни, амплитудата ще бъде два пъти по-голяма от амплитудата на оригиналните вълни, защото 2 cos(0) = 2. В другия краен вариант, когато (T2-T1) = 1 / (2 f) (двете вълни са с обратна фаза, защото цикълът на вълната е 1 / f единици на време и 1 / (2 f) е половината от цикъла), вълните ще се унищожат, защото 2 cos(π /2) = 0.
Една сложна звукова вълна може да се състои от много прости вълни. Ако този сложен сигнал е изпратен към едно оборудване или софтуер и изходният сигнал е с различна фаза, трябва да внимаваме, ако искаме да съберем входния и изходния сигнал. Даже и ако промяната във фазата (фазовият спектър) е една и съща при всички честоти, тази промяна ще влияе различно на амплитудите на отделните честоти и така ще промени честотното съдържание на сигнала.
Пример: фазов спектър на един цифров нискочестотен филтър с краен импулсен спектър
Може да се покаже, че един цифров нискочестотен филтър с краен импулсен спектър, коефициентите на който са симетрични спрямо средата на филтъра, забавя входния сигнал с (N – 1) / 2 семпли, което е равно на (N – 1) / (2 fs) секунди, където fs е пробната честота. Това е фазовият спектър на филтъра. Подобно на параграфите по-горе, това забавяне във времето е забавяне във фазата от 2 π f (N – 1) / (2 fs) радиани. Това изглежда правдоподобно, защото когато f се увеличава, цикълът на вълната става по-малък и един и същи брой семпли произвеждат по-голямо забавяне във ъгъла. Най-интересното в тази формула е, че промяната във фазата е линейна спрямо f / fs. Така, може да се каже, че този филтър има "линейна фаза".
Фазовият спектър на един примерен филтър с N = 20 е показан по-долу. Забележи, че този фазов спектър е показан спрямо (f / fs) (в хоризонталната ос). Според теоремата на Найкуист, Шанон и Котелников, f / fs не може да надвишава 0.5. Забележи също така, че фазовият спектър е отрицателен, което показва забавянето.
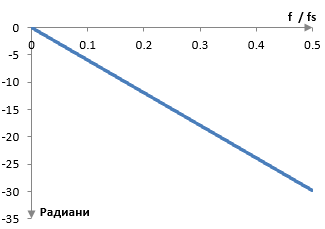
Тъй като една честота е просто една синусоида, едно забавяне от, да кажем, 2 π е същото като едно забавяне от нула. Едно забавяне от 2 π означава, че вълната ще започне точно с един цикъл по-късно, което означава, че вълната ще е същата, като една вълна която изобщо не е забавена. Тъй като синусоидите са периодични, можем да махнем пълните цикли от забавянето във фазовия спектър. Например, едно забавяне от 10 радиана е забавяне от 10 = 2 π + 3.71, което е същото като едно забавяне от 3.71 радиани. Тогава можем да представим фазовия спектър и както в следната графика.
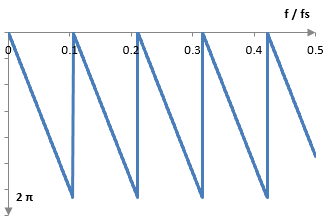
Фазов спектър при дадена трансферна функция
Фазовият спектър на една система с трансферната функция H, при честотата ω, е
$$\Phi(\omega) = \mathrm{arg}(H)$$
Това следва директно от определението на трансферната функция (виж Трансферна функция)). Функцията "arg" дава ъгъла между комплексното число H и хоризонталната ос. Когато Re{H} > 0 например arg{H} = arctan( Im{H} / Re{H} ).
Фазов спектър на филтри с ограничени импулсни спектри и със симетрични коефициенти
Вземи един филтър с краен (ограничен) импулсен спектър и с коефициенти a(k), които са симетрични спрямо средата (т.е., a(k) = a(N – 1 – k), k = 0, …, N-1).
Този филтър изчислява своят изходен сигнал y(n) от входния сигнал x(n) с формулата
$$y(n)= \sum_{k=0}^{N-1} a(k) \, x(n-k)$$
и неговата трансферна функция с преобразуването Z H(z), изчислена при честоти с амплитуда 1 (при z = ej ω), е
$$H(e^{j \, \omega} )= \sum_{k=0}^{N-1} a(k) \, z^{-k}= \sum_{k=0}^{N-1} a(k) \, e^{-j \,k \, \omega}$$ $$= \sum_{k=0}^{N-1} a(k) \, \cos(k \, \omega) - j \sum_{k=0}^{N-1} a(k) \, \sin(k \, \omega)$$
Тогава
$$\Phi(\omega) = \mathrm{arctan}(-\frac{\sum_{k=0}^{N-1} a(k) \sin(\omega k)}{\sum_{k=0}^{N-1} a(k) \cos(\omega k)}) = - \mathrm{arctan}(\frac{\sum_{k=0}^{N-1} a(k) \sin(\omega k)}{\sum_{k=0}^{N-1} a(k) \cos(\omega k)})$$
(Функцията arg не дава винаги arctan, така че тези изчисления са малко опростени.) В сумата в числителя можем да вземем всеки два аргумента с равни коефициенти a(k) и a(N – 1 – k) и да изчислим
$$a(k) \sin(\omega k) + a(N – 1 – k) \sin(\omega (N – 1 – k)) $$ $$ = a(k) (\sin(\omega k) + \sin(\omega (N – 1 – k))) $$ $$ = 2 a(k) \sin(\omega \frac{N – 1}{2}) \cos(\omega \frac{N – 1 – 2 k}{2})$$
В знаменателя, всеки два аргумента с равни коефициенти по същия начин дават
$$a(k) \cos(\omega k) + a(N – 1 – k) \cos(\omega (N – 1 – k)) $$ $$= 2 a(k) \cos(\omega \frac{N – 1}{2}) \cos(\omega \frac{N – 1 – 2 k}{2})$$
и фазовият спектър е
$$\Phi(\omega)= - \mathrm{arctan}(\frac{2 \sin(\omega \frac{N-1}{2})(1+\sum_{k=0}^{(N-1)/2}(a(k) \cos(\omega \frac{N-1-2k}{2}))))}{2 \cos(\omega \frac{N-1}{2})(1+\sum_{k=0}^{(N-1)/2}(a(k) \cos(\omega \frac{N-1-2k}{2}))))})$$
"1 + " е там, защото предполагаме, че филтърът има нечетен брой коефициенти N. Ако N е четно, тогава изчисленията са същите, но без "1 + ". Тогава
$$\Phi(\omega)= - \mathrm{arctan}(\frac{\sin(\omega \frac{N-1}{2})}{\cos(\omega \frac{N-1}{2})})= -\omega \frac{N-1}{2}$$
Това е същият резултат, който бе обяснен по-горе без да бъде доказан (ω = 2 π f / fs). Така, фазовият спектър на един филтър с ограничен импулсен спектър и с коефициенти, които са симетрични спрямо средата, е линеен спрямо ъгловата честота ω.
Добави нов коментар