The Bessel filter is given by the normalized transfer function
$$H(S)=\frac{c_{n,0}}{q_n(S)}$$
where n is the order of the filter and qn are the Bessel polynomials
$$q_n(S)=\sum_{k=0}^{n}c_{n,k}S^k$$
with coefficients
$$c_{n,k}=\frac{(2n-k)!}{2^{n-k}k!(n-k)!}$$
The transfer function above is normalized (i.e., it is presented for the Bessel low pass filter with cutoff frequency 1). The Bessel low pass filter can be obtained from the transfer function above with the substitution S = s / ωc, where s = jω, ωc is the cutoff frequency of the filter, and ω is the angular frequency spanning the frequency spectrum between 0 and π. The substitution S = ωc / s produces the Bessel high pass filter. The substitution S = (s2 + ωc2) / (B s) produces the Bessel band pass filter, where ωc is the midpoint of the pass band and B is the width of the band. The substitution S = B s / (s2 + ωc2) produces the Bessel band stop filter.
The Bessel filter is said to have an almost flat group delay (delay of the amplitude envelope for various frequencies). In other words, the Bessel filter has close to the same delay for all frequencies.
Example: High pass Bessel filter of the third order
Set n = 3 and use the substitution S = ωc / s. The transfer function of the third order Bessel high pass filter is
$$H(s)=\frac{15s^3}{\omega_c^3+6\omega_c^2s+15\omega_cs^2+15s^3}$$
The bilinear transformation s = 2 (z – 1) / (z + 1) allows us to rewrite the transfer function using the Z transform as follows.
$$H(z)=\frac{a_0+a_1z^{-1}+a_2z^{-2}+a_3z^{-3}}{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}}$$ $$a_0=120$$ $$a_1=-360$$ $$a_2=360$$ $$a_3=-120$$ $$b_0=\omega_c^3+12\omega_c^2+60\omega_c+120$$ $$b_1=3\omega_c^3+12\omega_c^2-60\omega_c-360$$ $$b_2=3\omega_c^3-12\omega_c^2-60\omega_c+360$$ $$b_3=\omega_c^3-12\omega_c^2+60\omega_c-120$$
Say that the cutoff frequency of the filter is ωc = 0.6 (technically, ωc = 2 arctan(0.6/2) ≈ 0.583, because of the warping of the frequency domain by the bilinear transformation). The transfer function of this example Bessel high pass filter is
$$H(z)=\frac{0.747496-2.242488z^{-1}+2.242488z^{-2}-0.747496z^{-3}}{1-2.435790z^{-1}+1.995366z^{-2}-0.548811z^{-3}}$$
and the filter itself is
$$y(k) = 0.747496 x(k) – 2.242488 x(k – 1) + 2.242488 x(k – 2) - 0.747496 x(k – 3)$$ $$+ 2.435790 y(k – 1) - 1.995366 y(k – 2) + 0.548811 y(k – 3)$$
Suppose that the sampling frequency is 2000 Hz. The cutoff frequency then is ωc = (0.6 * 2000) / (2 π) = 191 Hz. The magnitude response of the filter is shown in the graph below.
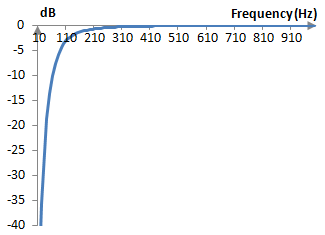
Example: Band stop Bessel filter of the second order
Set n = 2 and S = B s / (s2 + ωc2). The transfer function of the second order band stop Bessel filter is
$$H(s) = \frac{3s^4+6\omega_c^2s^2+3\omega_c^4}{3s^4+3B s^3+(B^2+6\omega_c^2)s^2+3B\omega_c^2s+3\omega_c^4}$$
After the bilinear transformation s = 2 (z – 1) / (z + 1), the transfer function becomes
$$H(z) = \frac{a_0+a_1z^{-1}+a_2z^{-2}+a_3z^{-3}+a_4z^{-4}}{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}+b_4z^{-4}}$$ $$a_0=48+24\omega_c^2+3\omega_c^4$$ $$a_1=-192+12\omega_c^4$$ $$a_2=288-48\omega_c^2+18\omega_c^4$$ $$a_3=-192+12\omega_c^4$$ $$a_4=48+24\omega_c^2+3\omega_c^4$$ $$b_0=48+24B+4B^2+24\omega_c^2+6B\omega_c^2+3\omega_c^4$$ $$b_1=-192-48B+12B\omega_c^2+12\omega_c^4$$ $$b_2=288-8B^2-48\omega_c^2+18\omega_c^4$$ $$b_3=-192+48B-12B\omega_c^2+12\omega_c^4$$ $$b_4=48-24B+4B^2+24\omega_c^2-6B\omega_c^2+3\omega_c^4$$
If, for example, we use the midpoint frequency ωc = 0.6 and the stop band width B = 1, and we scale the coefficients to obtain b0 = 1, then a0 = a4 = 0.654084, a1 = a3 = -2.184281, a2 = 3.131742, b0 = 1, b1 = -2.685262, b2 = 3.039987, b3 = -1.683299, b4 = 0.399923. If we suppose that the sampling frequency is 2000 Hz, then ωc = (0.6 * 2000) / (2 π) = 191 Hz, B = (1 * 2000) / (2 π) = 318 Hz and the magnitude response of the filter is as follows.
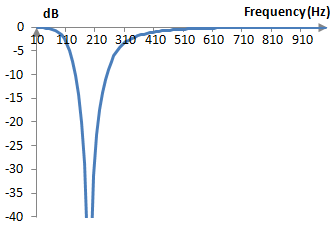
Phase response of the Bessel filter
The Bessel filter is said to have an almost flat group delay (delay of the amplitude envelope for various frequencies). In other words, the Bessel filter has close to a linear phase response. A comparison of the phase delay for the second order low pass Bessel filter and the second order low pass Butterworth filter is shown below.
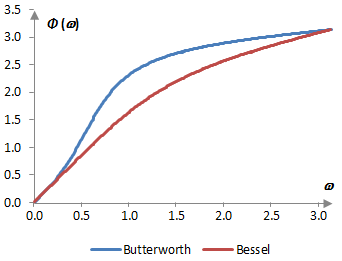
Comments
Error on sigma limits?
When specifying qn(S), your equation shows summing results from k=1 to k=n. Should this not be from k=0 to k=n, otherwise we're missing a term in the resulting polynomial?
Right
Right. I corrected the qn sum above to start from 0
Add new comment