Филтърът на Бесел се дава от нормализираната трансферна функция
$$H(S)=\frac{c_{n,0}}{q_n(S)}$$
където n е разряда на филтъра и qn са полиномите на Бесел
$$q_n(S)=\sum_{k=0}^{n}c_{n,k}S^k$$
с коефициенти
$$c_{n,k}=\frac{(2n-k)!}{2^{n-k}k!(n-k)!}$$
Трансферната фуникция по-горе е нормализирана (т.е., дадена е за нискочестотния филтър на Бесел с преходна честота 1). Нискочестотният филтър на Бесел се получава от трансферната функция по-горе, като се замести S = s / ωc, където s = jω, ωc е преходната честота на филтъра и ω е ъгловата честота в честотния диапазон между 0 и π. Заместването S = ωc / s произвежда високочестотния филтър на Бесел. Заместването S = (s2 + ωc2) / (B s) произвежда филтъра на Бесел, който пропуска някаква честотна лента (средночестотен), където ωc е средата на тази честотна лента и B е ширината на лентата. Заместването S = B s / (s2 + ωc2) произвежда филтъра на Бесел, който спира някаква честотна лента (режекторен).
Може да се каже, че филтърът на Бесел има почти плоско групово забавяне (забавяне на обвивките на амплитудите при различни честоти). С други думи, филтърът на Бесел има почти едно и също забавяне за всички честоти.
Пример: Високочестотен филтър на Бесел от трети разряд
Използваме n = 3 и S = ωc / s. Трансферната функция на високочестотния филтър на Бесел от трети разряд е
$$H(s)=\frac{15s^3}{\omega_c^3+6\omega_c^2s+15\omega_cs^2+15s^3}$$
Билинейното преобразуване s = 2 (z – 1) / (z + 1) ни позволява да запишем трансферната функция с преобразуването Z по следния начин.
$$H(z)=\frac{a_0+a_1z^{-1}+a_2z^{-2}+a_3z^{-3}}{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}}$$ $$a_0=120$$ $$a_1=-360$$ $$a_2=360$$ $$a_3=-120$$ $$b_0=\omega_c^3+12\omega_c^2+60\omega_c+120$$ $$b_1=3\omega_c^3+12\omega_c^2-60\omega_c-360$$ $$b_2=3\omega_c^3-12\omega_c^2-60\omega_c+360$$ $$b_3=\omega_c^3-12\omega_c^2+60\omega_c-120$$
Да кажем, че преходната честота на филтъра е ωc = 0.6 (по принцип, ωc = 2 arctan(0.6/2) ≈ 0.583, заради изкривяването на честотния диапазон от билинейното преобразуване). Трансферната функция на този примерен високочестотен филтър на Бесел е
$$H(z)=\frac{0.747496-2.242488z^{-1}+2.242488z^{-2}-0.747496z^{-3}}{1-2.435790z^{-1}+1.995366z^{-2}-0.548811z^{-3}}$$
и самият филтър е
$$y(k) = 0.747496 x(k) – 2.242488 x(k – 1) + 2.242488 x(k – 2) - 0.747496 x(k – 3)$$ $$+ 2.435790 y(k – 1) - 1.995366 y(k – 2) + 0.548811 y(k – 3)$$
Да предположим, че пробната честота е 2000 Hz. Преходната честота тогава е ωc = (0.6 * 2000) / (2 π) = 191 Hz. Амплитудният спектър на този филтър е показан в графиката по-долу.
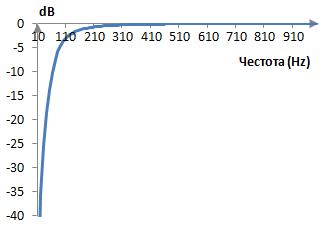
Пример: Филтър на Бесел от втори разряд за спирането на една честотна лента
Използваме n = 2 и S = B s / (s2 + ωc2). Трансферната функция на този филтър на Бесел от втори разряд за спирането на лентата е
$$H(s) = \frac{3s^4+6\omega_c^2s^2+3\omega_c^4}{3s^4+3B s^3+(B^2+6\omega_c^2)s^2+3B\omega_c^2s+3\omega_c^4}$$
След билинейното преобразуване s = 2 (z – 1) / (z + 1), трансферната функция става
$$H(z) = \frac{a_0+a_1z^{-1}+a_2z^{-2}+a_3z^{-3}+a_4z^{-4}}{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}+b_4z^{-4}}$$ $$a_0=48+24\omega_c^2+3\omega_c^4$$ $$a_1=-192+12\omega_c^4$$ $$a_2=288-48\omega_c^2+18\omega_c^4$$ $$a_3=-192+12\omega_c^4$$ $$a_4=48+24\omega_c^2+3\omega_c^4$$ $$b_0=48+24B+4B^2+24\omega_c^2+6B\omega_c^2+3\omega_c^4$$ $$b_1=-192-48B+12B\omega_c^2+12\omega_c^4$$ $$b_2=288-8B^2-48\omega_c^2+18\omega_c^4$$ $$b_3=-192+48B-12B\omega_c^2+12\omega_c^4$$ $$b_4=48-24B+4B^2+24\omega_c^2-6B\omega_c^2+3\omega_c^4$$
Ако използваме например средата на лентата на спиране ωc = 0.6 и ширината на лентата B = 1 и умножим коефициентите по една и съща скаларна величина за да получим b0 = 1, тогава a0 = a4 = 0.654084, a1 = a3 = -2.184281, a2 = 3.131742, b0 = 1, b1 = -2.685262, b2 = 3.039987, b3 = -1.683299, b4 = 0.399923. Ако предположим, че пробната честота е 2000 Hz, тогава ωc = (0.6 * 2000) / (2 π) = 191 Hz, B = (1 * 2000) / (2 π) = 318 Hz и амплитудният спектър на този филтър е следния.
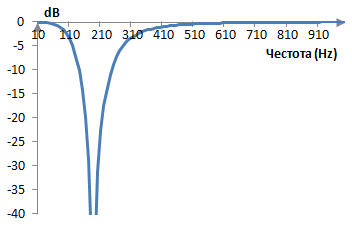
Фазов спектър на филтъра на Бесел
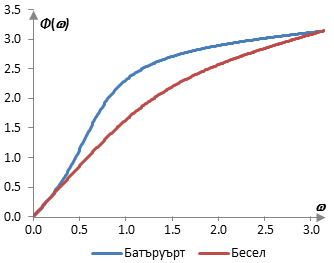
Може да се каже, че филтърът на Бесел има почти плоско групово забавяне (забавяне в амплитудната обвивка за различните честоти). С други думи, фазовият спектър на филтъра на Бесел е почти линеен. Следната графика сравнява фазовото забавяне при нискочестотния филтър на Бесел от втори разряд и нискочестотния филтър на Батъруърт от втори разряд.
Добави нов коментар