A peak filter is a frequency filter that passes a narrow band of frequencies and stops all other frequencies.
A peak filter is, in essence, a very narrow band pass filter and the opposite of a notch filter. An example peak filter is below.
Peak filters are used, for example, in wah wah effects. The wah wah effect is created by moving the peak filter up and down the frequency range and adding the filter output signal to the original signal.
An example digital IIR peak filter
A band-boost shelving filter with a narrow band a large gain is a peak filter. Take, for example, the second order low-boost infinite impulse response shelving filter transfer function with the Laplace transform
$$H(s)=\frac{s^2+\sqrt{2G}s+G}{s^2+\sqrt{2}s+1}$$
and substitute s with (s2+ωc2) / (B s). A band-boost shelving filter preserves the magnitude of frequencies outside of a band and increases the magnitude of frequencies inside the band by the gain G. If, instead, we want to preserve the magnitude of frequencies inside the band and reduce the magnitude of frequencies outside of the band, we will also need to add the gain (1/G). The result is the transfer function
$$H(s)=\frac{1}{G}\frac{(s^2+\omega_c^2)^2+\sqrt{2G}Bs(s^2+\omega_c^2)+GB^2s^2}{(s^2+\omega_c^2)^2+\sqrt{2}Bs(s^2+\omega_c^2)+B^2s^2}$$
Here, ωc is the mid-point of the frequency band with preserved magnitude, B is the width of that band, and G is the reduction in the gain for frequencies outside of the band.
After the bilinear transformation s = 2 (z – 1) / (z + 1), the transfer function of this filter is
$$H(s)=\frac{a_0+a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}+a_4 z^{-4}}{b_0+b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}+b_4 z^{-4}}$$ $$a_0=\frac{1}{G}(16+\omega_c^4+8 \omega_c^2+8\sqrt{2G} B+2\sqrt{2G} B \omega_c^2+4GB^2)$$ $$a_1=\frac{1}{G} (-64+4 \omega_c^4-16 \sqrt{2G} B+4\sqrt{2G} B \omega_c^2)$$ $$a_2=\frac{1}{G} (96+6 \omega_c^4-16 \omega_c^2-8GB^2)$$ $$a_3=\frac{1}{G} (-64+4 \omega_c^4+16 \sqrt{2G} B-4 \sqrt{2G} B \omega_c^2)$$ $$a_4=\frac{1}{G} (16+ \omega_c^4+8 \omega_c^2+2 \sqrt{2G} B(-4- \omega_c^2 )+4GB^2)$$ $$b_0=16+ \omega_c^4+8 \omega_c^2+8 \sqrt{2} B+2 \sqrt{2} B \omega_c^2+4B^2$$ $$b_1=-64+4 \omega_c^4-16 \sqrt{2} B+4 \sqrt{2} B \omega_c^2$$ $$b_2=96+6 \omega_c^4-16 \omega_c^2-8B^2$$ $$b_3=-64+4 \omega_c^4+16 \sqrt{2} B-4 \sqrt{2} B \omega_c^2$$ $$b_4=16+ \omega_c^4+8 \omega_c^2+2 \sqrt{2} B(-4- \omega_c^2 )+4B^2$$
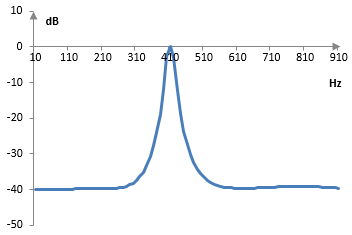
Take, for example, ωc = 1.5, B = 0.1, and G = 100 ≈ 40 dB. After scaling the filter coefficients to set b0 = 1, we have approximately a0 = 0.0149, a1 = -0.0131, a2 = 0.0202, a3 = -0.0083, a4 = 0.0062, b0 = 1, b1 = -1.0947, b2 = 2.2093, b3 = -1.0462, and b4 = 0.9135. If, for example, we set the sampling rate to 2000 Hz, then the mid-point of the band should be ≈ 477 Hz, but since the bilinear transformation warps the frequency domain, the actual midpoint of the pass band will be 2 arctan(ωc / 2) = 1.287 ≈ 410 Hz (if we want a filter precisely at the angular frequency 1.5, we should set ωc = 2 tan(1.5 / 2)). The magnitude response of this peak filter is as follows.
Add new comment