Филтър връх

Един филтър връх е честотен филтър, който пропуска една тясна честотна лента и спира всички други честоти.

Един филтър връх по същество е един много тесен средночестотен филтър и е обратното на един филтър бразда. Един примерен филтър връх е показан по-долу.

Филтрите връх се използват например при ефектите уа-уа. Ефектът уа уа се създава като се мести филтъра връх нагоре и надолу в честотния диапазон и изходният сигнал от филтъра се добавя към оригиналния сигнал.

Един примерен цифров филтър връх с неограничен импулсен спектър

Един средночестотен филтър шелф с тясна лента и голяма допълнителна амплитуда е филтър връх. Вземи например нискочестотния филтър шелф от втори разряд с неограничен импулсен спектър с трансферната функция с преобразуването на Лаплас

$$H(s)=\frac{s^2+\sqrt{2G}s+G}{s^2+\sqrt{2}s+1}$$

и замести s със (s²+ω_c²) / (B s). Един средночестотен филтър шелф запазва амплитудата на честотите извън една лента и увеличава амплитудата на честотите в лентата с амплитудата G. Ако вместо това искаме да запазим амплитудата на честотите в лентата и да намалим амплитудите на честотите извън лентата, трябва също да добавим амплитудата (1/G). Резултатът е трансферната функция

$$H(s)=\frac{1}{G}\frac{(s^2+\omega_c^2)^2+\sqrt{2G}Bs(s^2+\omega_c^2)+GB^2s^2}{(s^2+\omega_c^2)^2+\sqrt{2}Bs(s^2+\omega_c^2)+B^2s^2}$$

Тук, ω_c е средата на честотната лента със запазена амплитуда, B е ширината на тази лента и G е намалението на амплитудите на честотите извън лентата.

След билинейното преобразуване s = 2 (z – 1) / (z + 1), трансферната функция на филтъра е

$$H(s)=\frac{a_0+a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}+a_4 z^{-4}}{b_0+b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}+b_4 z^{-4}}$$ $$a_0=\frac{1}{G}(16+\omega_c^4+8 \omega_c^2+8\sqrt{2G} B+2\sqrt{2G} B \omega_c^2+4GB^2)$$ $$a_1=\frac{1}{G} (-64+4 \omega_c^4-16 \sqrt{2G} B+4\sqrt{2G} B \omega_c^2)$$ $$a_2=\frac{1}{G} (96+6 \omega_c^4-16 \omega_c^2-8GB^2)$$ $$a_3=\frac{1}{G} (-64+4 \omega_c^4+16 \sqrt{2G} B-4 \sqrt{2G} B \omega_c^2)$$ $$a_4=\frac{1}{G} (16+ \omega_c^4+8 \omega_c^2+2 \sqrt{2G} B(-4- \omega_c^2 )+4GB^2)$$ $$b_0=16+ \omega_c^4+8 \omega_c^2+8 \sqrt{2} B+2 \sqrt{2} B \omega_c^2+4B^2$$ $$b_1=-64+4 \omega_c^4-16 \sqrt{2} B+4 \sqrt{2} B \omega_c^2$$ $$b_2=96+6 \omega_c^4-16 \omega_c^2-8B^2$$ $$b_3=-64+4 \omega_c^4+16 \sqrt{2} B-4 \sqrt{2} B \omega_c^2$$ $$b_4=16+ \omega_c^4+8 \omega_c^2+2 \sqrt{2} B(-4- \omega_c^2 )+4B^2$$

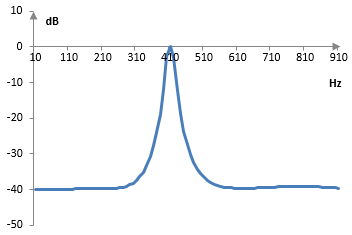
Вземи например ω_c = 1.5, B = 0.1 и G = 100 ≈ 40 dB. След като умножим коефициентите на филтъра по една и съща скаларна величина за да получим b₀ = 1, ще имаме приблизително a₀ = 0.0149, a₁ = -0.0131, a₂ = 0.0202, a₃ = -0.0083, a₄ = 0.0062, b₀ = 1, b₁ = -1.0947, b₂ = 2.2093, b₃ = -1.0462 и b₄ = 0.9135. Ако например вземем пробната честота 2000 Hz, тогава средата на лентата трябва да е ≈ 477 Hz, но тъй като билинейното преобразуване изкривява честотния диапазон, действителната среда на лентата ще е 2 arctan(ω_c / 2) = 1.287 ≈ 410 Hz (ако искаме един филтър точно при ъгловата честота 1.5, трябва да използваме ω_c = 2 tan(1.5 / 2)). Амплитудният спектър на този филтър връх е следния.