A shelving filter is a frequency filter that boosts or cuts the magnitude of frequencies in a frequency band.
For example, a low-boost shelving filter will increase the magnitude of frequencies below some cutoff frequency and preserve the magnitude of frequencies above the cutoff frequency. Such a filter will, in essence, act similarly to a low pass filter, but with a smaller difference between the magnitudes of the low frequency band and the high frequency band.
Digital FIR shelving filter
A finite impulse response (FIR) shelving filter can be created by combining low pass, high pass, band pass, and band stop FIR filters and with appropriate gain. The two-band equalizer in the topic Equalizer is a high-boost shelving filter, as it increases the magnitude of frequencies above the cutoff frequency and leaves the magnitudes of frequencies below the cutoff frequency unchanged.
Digital IIR low-boost shelving filter
The function
$$H(s)=\prod_{n=1}^N \frac{s+\sqrt[\leftroot{-2}\uproot{4}N]{G}e^{-j \,a_n}}{s+e^{-j \,a_n}}, \,\,\, a_n=(\frac{1}{2}-\frac{2n-1}{2N})\pi$$
is a transfer function with the Laplace transform for a low-boost shelving filter of order N with the cutoff frequency 1 and gain G.
The magnitude response of the low-boost shelving filter of order N above is
$$|H(j\,\omega)H(-j\,\omega)|=\frac{\omega^{2N}+G^2}{\omega^{2N}+1}$$
Set, for example, N = 2. The Laplace transform transfer function of the second order low-boost shelving filter with gain G is
$$H(s)=\frac{s^2+\sqrt{2G}\,s+G}{s^2+\sqrt{2}\,s+1}$$
To produce the Z transform transfer function of the filter for the cutoff frequency ωc, use the biquad transform s = (z – 1) / (K (z + 1)) (see also Bilinear transformation), where K = tan(ωc / 2).
$$H(z)= \frac{(1+\sqrt{2G}\,K+G\,K^2)+(-2+2G\,K^2)z^{-1}+(1-\sqrt{2G}\,K+G\,K^2)z^{-2}}{(1+\sqrt{2}\,K+K^2)+(-2+2K^2)z^{-1}+(1-\sqrt{2}\,K+K^2)z^{-2}}$$
Suppose the sampling rate is 2000 Hz, G = 2 (6 dB), and ωc = 0.6 (191 Hz for the sampling rate, K ≈ 0.30934). The magnitude response of the resulting filter is
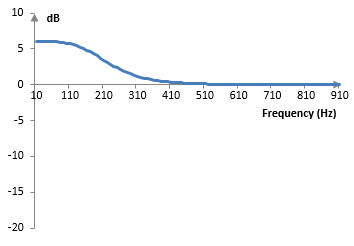
This filter will have a shorter transition band at higher orders.
Digital IIR high-cut shelving filter
A shelving filter that preserves the magnitude of low frequencies but reduces the magnitude of high frequencies is the same filter above, but with the additional gain (1/G). If, for example, we scale the coefficient of the numerator in the Z transform transfer function of the filter above by (1/G), we will get the following magnitude response.
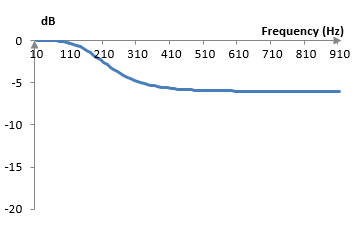
Digital IIR high-boost shelving filter
An easy way to obtain a shelving filter that preserves the magnitude of low frequencies but increases the magnitude of high frequencies is to switch the coefficients of the numerator and the denominator in the transfer function for the low boost filter and add additional gain of G. For example, a high-boost filter from the low-boost filter above is
$$H(z)=G\,\frac{(1+\sqrt{2}\,K+K^2)+(-2+2K^2)z^{-1}+(1-\sqrt{2}\,K+K^2)z^{-2}}{(1+\sqrt{2G}\,K+G\,K^2)+(-2+2G\,K^2)z^{-1}+(1-\sqrt{2G}\,K+G\,K^2)z^{-2}}$$
With the same parameters above (sampling rate of 2000 Hz, G = 2 ≈ 6 dB, and ωc = 0.6 (191 Hz for the sampling rate, K ≈ 0.30934), this filter will produce the following magnitude response.
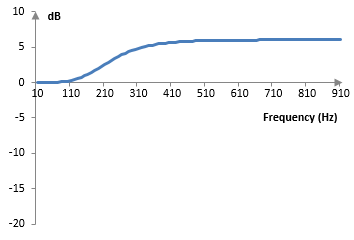
Digital IIR low-cut shelving filter
A low-cut shelving filter is simply a high-boost shelving filter with lower gain (i.e., with the gain 1/G applied to numerator coefficients).
Digital IIR band-boost and band-cut shelving filters
Band-boost and band-cut shelving filters can be produced with the right combination of low- and high- boost or cut shelving filters. Alternatively, a band-boost filter can be produced from the low-boost transfer function at the top of this topic, by substituting s with (s2+ωc2) / (B s), where ωc is the mid-point of the frequency band with a gain boost and B is the width of the band. A band-cut shelving filter can be produced if we switch the coefficients of the numerator and denominator of the band-boost shelving filter.
For example, substituting s with (s2+ωc2) / (B s) in the second order low-boost shelving filter, we get
$$H(s)=\frac{(\frac{s^2+\omega_c^2}{Bs})^2+\sqrt{2}\,G \frac{s^2+\omega_c^2}{Bs}+G}{(\frac{s^2+\omega_c^2}{Bs})^2+\sqrt{2} \frac{s^2+\omega_c^2}{Bs}+1}=\frac{(s^2+\omega_c^2)^2+\sqrt{2}\,G Bs(s^2+\omega_c^2)+GB^2 s^2}{(s^2+\omega_c^2)^2+\sqrt{2}\, Bs(s^2+\omega_c^2)+B^2 s^2}$$
After the bilinear transformation s = 2 (z – 1) / (z + 1), the transfer function of the band-boost shelving filter is
$$H(s)=\frac{a_0+a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}+a_4 z^{-4}}{b_0+b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}+b_4 z^{-4}}$$ $$a_0=16+\omega_c^4+8\omega_c^2+8\sqrt{2}\,G B+2\sqrt{2}\,G B\omega_c^2+4GB^2$$ $$a_1=-64+4\omega_c^4-16\sqrt{2}\,G B+4\sqrt{2}\,G B\omega_c^2$$ $$a_2=96+6\omega_c^4-16\omega_c^2-8G\,B^2$$ $$a_3=-64+4\omega_c^4+16\sqrt{2}\,G B-4\sqrt{2}\,G B \omega_c^2$$ $$a_4=16+\omega_c^4+8\omega_c^2+2\sqrt{2}\,G B(-4-\omega_c^2)+4GB^2$$ $$b_0=16+\omega_c^4+8\omega_c^2+8\sqrt{2}\, B+2\sqrt{2}\, B \omega_c^2+4B^2$$ $$b_1=-64+4\omega_c^4-16\sqrt{2}\, B+4\sqrt{2}\, B\omega_c^2$$ $$b_2=96+6\omega_c^4-16\omega_c^2-8B^2$$ $$b_3=-64+4\omega_c^4+16\sqrt{2}\, B-4\sqrt{2}\, B\omega_c^2$$ $$b_4=16+\omega_c^4+8\omega_c^2+2\sqrt{2}\, B(-4-\omega_c^2)+4B^2$$
The magnitude response of this filter, at the sampling rate 2000 Hz, ωc = 1.5 ≈ 477 Hz, B = 0.5, and G = 4 ≈ 12 dB, is as follows. Note that this filter is computed with the bilinear transformation and not with the biquad transform and so there is a shift in the ωc and B (see Bilinear transformation).
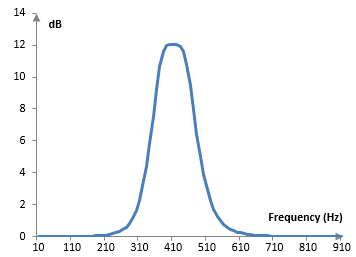
If the numerator and denominator coefficients of this filter are switched, the magnitude response of the filter will be as follows.
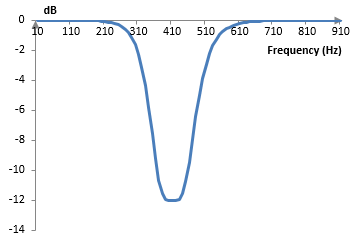
Note that, in this filter, one can control the mid-point of the affected band, the width of the band, and the gain of the band. If the band is narrow and the gain is large, the band-boos filter can become a peak filter and the band-cut filter can become a notch filter.
A note on narrow band shelving filters
Note that the magnitude response of the band boost and band cut shelving filter in the example above does not behave as well for very narrow bands. For example, the following is the magnitude response of the same band boost shelving filter above, with ωc = 2, B = 0.1, and G = 4, at the sampling rate 2000 Hz.
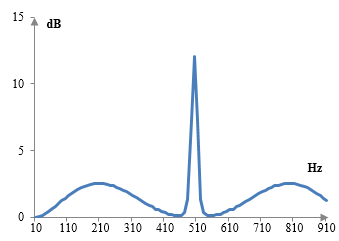
The ripples on both sides of the magnitude response will become larger at smaller values for B or larger values for ωc.
Add new comment