Доста от теорията за цифрови сигнали изисква работа с отрицателни честоти. Отрицателните честоти не означават нищо на практика и използването им при работата с цифрови сигнали създава проблем. Оказва се, обаче, че е лесно да се превърне един сигнал, който съдържа отрицателни честоти, в един сигнал, който не ги съдържа.
Едно преобразуване, което премахва отрицателните честоти от един аналитичен сигнал, се нарича преобразуване на Хилбърт.
Вземи един сигнал x(t), който съдържа положителните и отрицателните честоти ω и -ω.
$$x(t) =e^{j\,\omega\,t}+e^{-j\,\omega\,t}$$
Едно добро преобразуване на Хилбърт H(x(t)) е нещо, което отмества сигнала с -π / 2 при положителните честоти и с π / 2 при отрицателните честоти.
$$H(x(t)) =e^{j\,\omega\,t-\frac{\pi}{2}}+e^{-j\,\omega\,t+\frac{\pi}{2}}=-j\,e^{j\,\omega\,t}+j\,e^{-j\,\omega\,t}$$
Тогава
$$x(t)+j\,H(x(t)) =e^{j\,\omega\,t}+e^{-j\,\omega\,t}-j^2\,e^{j\,\omega\,t}+j^2\,e^{-j\,\omega\,t}=2\,e^{j\,\omega\,t}$$
Така, преобразуването на Хилбърт, умножено по j и добавено към оригиналния сигнал е интересно от аналитична гледна точка, защото може да се използва за да превърне един сигнал с положителни и отрицателни честоти в един сигнал, който съдържа само положителни честоти. Това преобразуване на Хилбърт е интересно и от практическа гледна точка, защото отмества положителните честоти с точно -π / 2 или с една четвърт от дължината на техния период.
Филтри с ограничени или неограничени импулсни спектри, които работят приблизително като едно преобразуване на Хилбърт, съществуват. Един от начините да се създаде един такъв филтър е да се използва желания честотен спектър на преобразуването
$$H(\omega)=\begin{cases} e^{j \frac{\pi}{2}}, \omega \lt 0 \\ 0, \omega=0 \\ e^{-j \frac{\pi}{2}}, \omega \gt 0 \end{cases}$$
или, по-точно, дискретизираната версия (за N нечетно)
$$H(k)=\begin{cases} j, k=1,2,...,\frac{N-1}{2} \\ 0, k=0 \\ -j, k=\frac{N+1}{2}, ..., N-1 \end{cases}$$
и да се използва дискретизираното обратно преобразуване на Фурие.
Получаваме преобразуването на Хилбърт
$$a(k)=\frac{1}{N} (\cot(\frac{\pi\,k}{2})-\frac{\cos(\pi\,k)}{\sin(\frac{\pi\,k}{N})})$$
Когато N е четно, можем по същия начин да получим
$$a(k)=\frac{2}{N} \sin^2(\frac{\pi\,k}{2})\,\cot(\frac{\pi\,k}{2})$$
И в двата случая, когато N е нечетно и когато N е четно, a(k) = 0 при k = 0, 2, 4, ….
За много къси преобразувания (например N = 10), преобразуването на Хилбърт може да се изчисли приблизително с
$$a(k)=\begin{cases} 0, k \,четно \\ \frac{2}{\pi\,k}, k\, нечетно \end{cases}$$
Едно преобразуване на Хилбърт като филтър с ограничен импулсен спектър и с дължина 101 е показано по-долу.
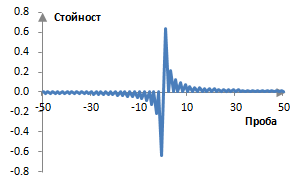
Следната графика показва, че този филтър измества една вълна от 100 Hz, дискретизирана с пробната честота 2000 Hz, с една четвърт от нейния цикъл.
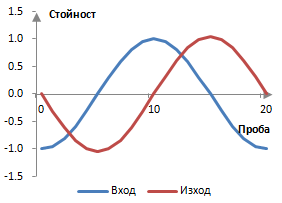
Тъй като филтърът е ограничен и не е идеален, не запазва амплитудата на всички честоти. Честотният (амплитудният) спектър на този примерен филтър в началото на честотния диапазон е следния.
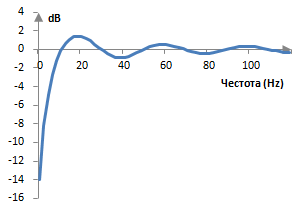
Този филтър има подобна загуба на амплитудата близо до половината от пробната честота. Това е един средночестотен филтър. Загубата на амплитуда в двата края на честотния диапазон е по-малка с по-дълги филтри и изчезва по-бързо в горния край на честотния диапазон и по-бавно в долния край. Честотния спектър на преобразуването на Хилбърт има характерните вълни на феномена на Гибс, които могат да се променят със същите прозорци, които се използват при други филтри с ограничени импулсни спектри.
Използване на преобразуването на Хилбърт
Тъй като преобразуването на Хилбърт измества всички честоти в сигнала с -π / 2, този филтър е идеален за намирането на амплитудната обвивка на сигнала. Амплитудната обвивка на една честота може да се изчисли с корена на сумата на квадрата на стойността на честотата при определената проба и квадрата на преобразуването на Хилбърт на честотата в тази проба.
Забележи обаче, че преобразуването на Хилбърт е един филтър с ограничен импулсен спектър и с коефициенти, които са симетрични спрямо средата и затова дава забавяне в сигнала след преобразуването от (N – 1) / 2 проби, където N е дължината на преобразуването на Хилбърт (за N нечетно; забавянето ще бъде N / 2 за N четно). Преди да изчислим амплитудната обвивка, трябва да забавим оригиналния сигнал. Изчислението за амплитудната обвивка е следното.
$$Обвивка=\sqrt{x(k-\frac{N-1}{2})^2+H(x(k))^2}$$
По-долната графиката показва един сложен сигнал x(k) дискретизиран с 2000 Hz и който се състои от две прости вълни с честоти 100 Hz и 130 Hz и с променяща се амплитуда. Амплитудната обвивка е изчислена с горната формула.
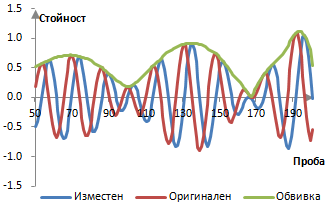
Амплитудните обвивки имат много приложения. В продуцирането на аудио, амплитудните обвивки се използват в компресорите на динамиката.
Добави нов коментар