Феномен на Гибс

В математиката, феномена на Гибс се появява, когато реда на Фурие – ред от непрекъснати функции – се използва като приближение към функция, която е с непрекъснати производни, но и с точка на прекъсване. При точката на прекъсване, частичната сума на реда на Фурие, вместо да се приближи към функцията с точка на прекъсване, създава вълни. Броя и честотата на тези вълни обикновено се увеличава, когато приближението се подобрява, тяхната енергия / амплитудата измерена със средното квадратично намалява, но те не изчезват, а се приближават към една определена височина.

При работата с цифрови сигнали, тъй като търсеният амплитуден спектър на един филтър с ограничен импулсен спектър обикновено е функция с точка на прекъсване, действителният амплитуден спектър на филтъра има вълни в точката на прекъсване, чиито брой и честота се увеличава с увеличаването на дължината на филтъра и чиято енергия намалява, но които не изчезват а запазват една определена височина от, както е показано по-долу, приблизително 0.08949 от нормализираната амплитуда. Тези вълни са израз на феномена на Гибс.

Феномена на Гибс при филтри с ограничени импулсни спектри

Предпочитаният амплитуден спектър на един нискочестотен филтър има точка на прекъсване, защото идеалният амплитуден спектър в честотния диапазон трябва да даде нормализираната амплитуда 1 (оригиналната амплитуда на сигнала) до преходната честота и амплитудата 0 след това. Следното е амплитудния спектър на един идеален нискочестотен филтър.

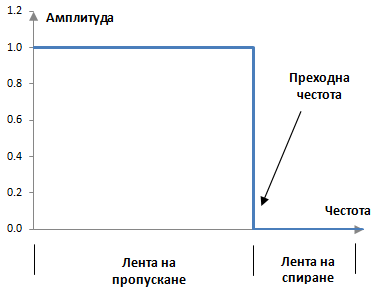
Следната графика показва типичният амплитуден спектър на един цифров нискочестотен филтър с ограничен импулсен спектър.

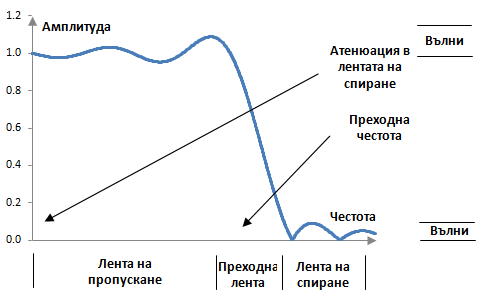
Амплитудният спектър на един типичен нискочестотен филтър с ограничен импулсен спектър по принцип е приближение към идеалния амплитуден спектър с реда на Фурие. Две извеждания на формулите за такива нискочестотни филтри са показани в темата Нискочестотен филтър. Вълните в лентата на пропускане и лентата на спиране в действителния амплитуден спектър са изражение на феномена на Гибс.

Следната графика сравнява амплитудните спектри в лентата на пропускане на три нискочестотни филтри с дължина 100 точки, 200 точки и 300 точки. И трите филтри използват преходната честота 40 Hz. пробната честота е 2000 Hz.

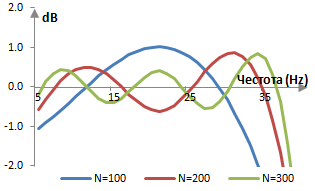
Един филтър с по-голяма дължина, амплитудният спектър на който е и по-добро приближение към идеалния търсен амплитуден спектър, дава повече, но по-малки вълни (с по-малко енергия). Когато дължината на филтъра се увеличава, вълните не изчезват, но се спиран на някаква определена крайна височина.

Един пример на феномена на Гибс в един еквилайзер

Един интересен пример за феномена на Гибс се проявява при еквилайзерите, създадени на базата на филтри с ограничени импулсни спектри. Следната графика показва амплитудните спектри на два филтъра – един нискочестотен и един високочестотен – с една и съща преходна честота равна на 40 Hz при пробната честота 2000 Hz. Амплитудата на високочестотния филтър е увеличена с 2 dB.

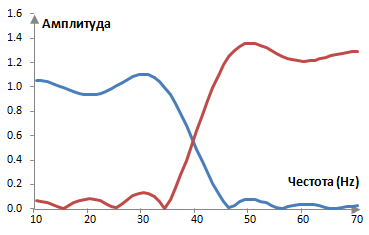
Когато двата филтъра са комбинират и техните коефициенти се събират, се получава един еквилайзер, който добавя 2 dB към честотите над 40 Hz. Амплитудният спектър на еквилайзера е следния.

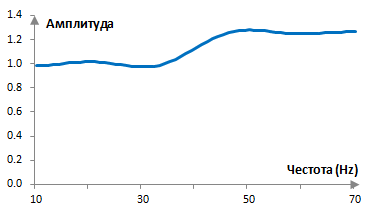
Вълните на еквилайзера са по-малки от вълните при всеки от отделните филтри. Както е показано по-долу, стойността, с която вълните на феномена на Гибс надвишават желания амплитуден спектър, е пропорционална на промяната в точката на прекъсване на амплитудния спектър (с множител от около 1.089494). Тъй като при точката на прекъсване желаният амплитуден спектър на еквилайзера разликата е малка (2 dB, от нормализираната амплитуда 1 до нормализираната амплитуда 1.259) в сравнение с разликите при точките на прекъсване на нискочестотния и високочестотния филтър (от нормализираната амплитуда 0 до нормализираната амплитуда 1), вълните са по-малки.

Стойност на феномена на Гибс

Един филтър a(k) с ограничен импулсен спектър и с дължина N изчислява стойностите на изходния сигнал y(k) от стойностите на входния сигнал x(k) с формулата

$$y(k)=\sum_{n=0}^{N-1} a(n) \, x(k-n)$$

Преобразуването Z на изхода на филтъра с ограничен импулсен спектър дава следното.

$$Z(y(k))=Z(\sum_{n=0}^{N-1} a(n) \, x(k-n))=Z(x(k)) \sum_{n=0}^{N-1} a(n) \, z^{-n}$$

Общата форма на трансферната функция на филтъра с ограничен импулсен спектър тогава е

$$H(z)=\sum_{k=0}^{N-1} a(k) \, z^{-k}$$

Един типичен филтър с ограничен импулсен спектър е такъв, че коефициентите му са симетрични спрямо средата, тъй като това дава линеен фазов спектър и филтър с реални коефициенти. Можем да комбинираме първия и последния коефициент, втория и предпоследния коефициент и така нататък, и да означим M = (N – 1) / 2. На кръга с радиус единица, при z = e^{-j ω}

$$a(k) \, z^{-k} + a(N-1-k) \, z^{k-(N-1)}$$ $$=z^{-M} \, a(k) \, (z^{M-k}+z^{k-M})$$ $$=2 z^{-M} \, a(k) \, \cos(\omega (k-M))$$

и амплитудният спектър, с по-горната трансферна функция, става

$$|H(e^{-j\,\omega})|=|z^{-M}(a(M)+2\sum_{k=0}^{M-1} a(k) \, \cos(\omega(k-M)))|$$ $$=a(M)+ 2\sum_{k=0}^{M-1} a(k) \, \cos(\omega(k-M))$$

Това е една непрекъсната функция с реални стойности. Тя ни позволява да представим феномена на Гибс. Преработваме амплитудния спектър, като използваме a(k) от формулата за нискочестотния филтър

$$a(k)=\begin{cases} \frac{\sin(\frac{2\pi\,f_c\,(k-\frac{N-1}{2})}{f_s})}{\pi(k-\frac{N-1}{2})}, k \ne \frac{N-1}{2} \\ 2\frac{f_c}{f_s}, k = \frac{N-1}{2} \end{cases}$$

където преходната честота е ω_c = 2 π f_c / f_s и заместваме n = K – M.

$$|H(e^{-j\,\omega})|=a(M) + 2 \sum_{k=0}^{M-1} \frac{\sin(\omega_c (k-M)) \, \cos(\omega (k-M))}{\pi(k-M)}$$ $$=a(M) + 2 \sum_{n=1}^{M} \frac{\sin(\omega_c\,n) \, \cos(\omega\,n)}{\pi\,n}$$ $$=a(M) + \frac{\omega_c+\omega}{\pi} \sum_{n=1}^{M} \frac{\sin((\omega_c+\omega)n)}{(\omega_c+\omega)n}+ \frac{\omega_c-\omega}{\pi} \sum_{n=1}^{M} \frac{\sin((\omega_c-\omega)n)}{(\omega_c-\omega)n}$$

Нека ω = ω_c + π / M. Втората сума по-горе става

$$\frac{1}{M} \sum_{n=1}^{M} \frac{\sin(\frac{\pi\,n}{M})}{\frac{\pi\,n}{M}}$$

Когато M става безкрайно голямо, ω се приближава към ω_c отдясно, сумата се приближава към познатия интеграл между 0 и 1 на функцията sinc

$$\int_{0}^{1} \frac{\sin(\pi\,t)}{\pi\,t} \approx \frac{1}{2} + 0.08949$$

и така

$$\lim_{\omega \rightarrow \omega_c+} |H(e^{-j\,\omega})|=a(M)+\frac{2\omega_c}{\pi} \sum_{n=0}^{M} \frac{\sin(2\omega_c\,n)}{2\omega_c\,n}-\frac{1}{2}-0.08949$$

Сега пък нека ω = ω_c – π / M. Същата втора сума по-горе е

$$-\frac{1}{M} \sum_{n=1}^{M} \frac{\sin(-\frac{\pi\,n}{M})}{-\frac{\pi\,n}{M}}$$

Когато M става безкрайно голямо и ω се приближава към ω_c този път отляво, сумата се приближава към

$$-\int_{0}^{1} \frac{\sin(\pi\,t)}{\pi\,t} \approx -(\frac{1}{2}+0.08949)$$

и така

$$\lim_{\omega \rightarrow \omega_c-} |H(e^{-j\,\omega})|=a(M)+\frac{2\omega_c}{\pi} \sum_{n=0}^{M} \frac{\sin(2\omega_c\,n)}{2\omega_c\,n}+\frac{1}{2}+0.08949$$

Двете граници се различават приблизително с 1.17898. Желаният амплитуден спектър, от друга страна, има разлика в точката на прекъсване само от 1. Това е феномена на Гибс.

Позиция на вълните

Това не означава непременно, че вълните на феномена на Гибс се получават точно при ω = ω_c +/- π / M. Ако искахме да намерим вълните, максимума на амплитудния спектър |H(e^{-j ω})|, вероятно ще започнем като изчислим производната на амплитудния спектър. Така, както той е изписан по-горе, производната на амплитудния спектър ще бъде една сума от косинуси, които могат да бъдат събрани с формулата на Диришле. Така изчислената производна обаче вероятно ще бъде прекалено сложна за нашата работа. Много по-лесно е да се намерят тези максимуми с цифрови методи – с програмиране.

По-долната графика показва нормализираната ъглова честота ω, при която се получават максимумите на амплитудните спектри на филтри с различна дължина N.

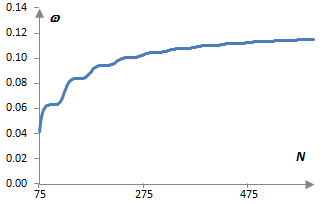
Това са нискочестотни филтри с преходна честота f_c = 40 Hz при пробната честота f_s = 2000 Hz. С увеличаването на дължината на филтрите, ω се приближава към нормализираната преходна честота ω_c = 2π f_c / f_s = 0.126. Стълбовидното поведение на графиката се дължи на това, че работим само с цели числа N. Стойностите за N < 75 не са показани, защото при тези филтри няма вълни. Техните амплитудни спектри започват под 1 и продължават надолу с по-големите честоти.

Смекчаване на вълните на феномена на Гибс

Вълните на феномена на Гибс могат да се смекчат с прилагането на прозорци върху филтрите с ограничени импулсни спектри. Могат да се използват например прозорците на Блекмън, Хан, Хеминг, Тъки, Гаус, Кайзер и много други. Прозорците, въпреки че намаляват вълните и обикновено подобряват атенюацията в лентата на спиране, жертват (увеличават) преходната лента на филтъра.